Buckling analysis of corrugated pipings subjected to external pressure and surrounded by elastic medium

MS. Pham Thanh Hieu MS. Nguyen Thi Giang DR. Vu Hoai Nam DR. Nguyen Thi Phuong University of Transport Technology Revewer: DR. Nguyen Minh Khoa DR. Tran Trung Hieu

ABSTRACT: A new approach of elastic stability of trapezoidal and round corrugated metal pipings for construction structures is proposed in this paper. By using Donnell shell theory and the homogenization theory of corrugated structure proposed by Xia et al.[1], the governing equations of piping subjected to external pressure and surrounded by Pasternak’s elastic foundation are established. The obtained equilibrium equation system is directly solved to obtain the explicit form of critical load of piping. The numerical investigations evaluated carrying capacity of corrugated piping structures and offed remarks of application of this structure.

KEYWORDS: Corrugated piping, buckling, external pressure, elastic foundation.

1. INTROCDUCTION

Corrugated piping structures are important components widely used as major load carrying portions in the structures of road and bridge, building and mechanical engineering. Their static and dynamic behavior are important and have received considerable attention in the world. Samanta and Mukhopadhyay [2] presented the mechanic response analyses of trapezoidal corrugated sheets by considering both extensional and flexural rigidities. Peng et al. [3] proposed an equivalent elastic property theory of sinusoidal and trapezoidal corrugated plates by mesh-free Galerkin method. Yokozeki et al. [4] investigated the mechanic properties of composite corrugated by experiment and analysis. Kress and Winkler [5 and 6] investigated accurate analytical expressions of equivalent orthotropic plates. The homogenized plate properties for a morphing aircraft shells to experimental results is compared by Thill et al. [7 and 8]. Kress and Winkler [9] used a two dimensions finite element to investigate mechanic behavior of corrugated laminate structures. Recently, Hieu et al. [10] studied elastic stability of trapezoidal corrugated metal pipings without elastic foundation by using Donnell shell theory and Samanta and Mukhopadhyay’s homogenization theory.

An analytical approach of buckling analysis of trapezoidal and round corrugated piping subjected to external pressure and surrounded by Pasternak two-parameter elastic foundation is presented in this paper. By using Donnell shell theory and Xia et al.’s homogenization theory [1], the explicit form of critical load of piping is obtained. The numerical investigations evaluated carrying capacity of corrugated piping structures and offed a significant remark in application.

2. THEORICAL FORMULATION

Consider the trapezoidal and round corrugated piping of length l, radius of curvature r and thickness h as shown in figure 1. The shell is surrounded by a Pasternak’s two-parameter elastic foundation with K₁(N/m³) is Winkler foundation modulus and K₂(N/m)is the shear layer foundation stiffness of Pasternak model

 

 

 

 

 

 

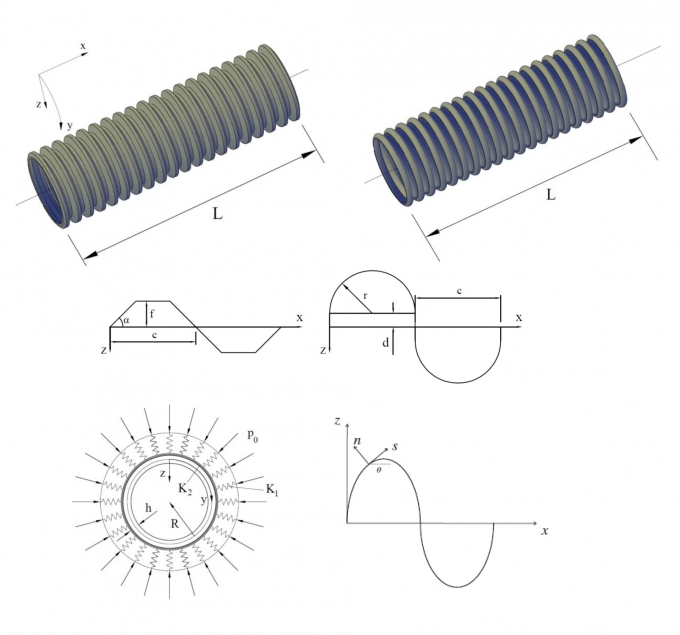Figure 2.1: Geometry and coordinate system of trapezoidal and round corrugated pipings

By using the homogenization theory proposed by Xia et al. [1], the expressions for force and moment resultants are obtained

where

 

 

 

 

 

 

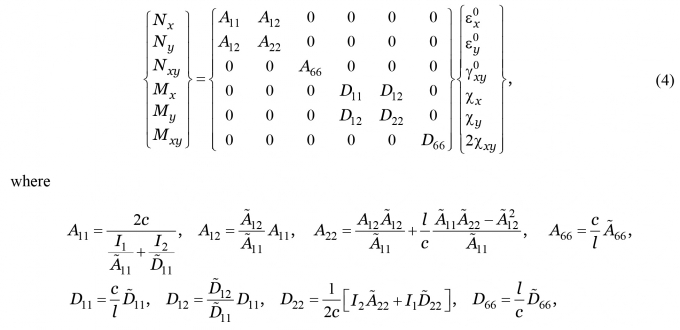and

 

 

 

 

 

 

 

Stability equations of piping may be established by the adjacent equilibrium criterion. It is assumed that equilibrium state of the piping under applied load is presented by displacement component u₀, v₀, w₀. The state of adjacent equilibrium differs that of stable equilibrium by u_*, v_*, and w_* and the total displacement components of a neighboring configuration are:

 

 

 

 

 

 

 

Considering the first two of Eqs.(8), a stress function may be defined as:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

where

 

 

 

 

 

 

3. NUMERICAL INVESTIGATIONS AND DISCUSSIONS

To validate the present formulation, the elastic critical buckling load of trapezoidal corrugated pipings is considered in Table 3.1, which were also analyzed by Hieu et al. [10] by using Samanta and Mukhopadhyay’s homogenization theory. As can be seen, the good agreements are obtained in these comparisons.

Consider corrugated pipings made from the steel with the following propeties  E = 21,0 x 10¹⁰ N/m², v = 0,3 and geometric parameters R = 0,3m, h = 0,005m, L = 3m, c = 0,03m. The isotropic pipings are made from same material with corrugated pipings and geometric parameters R = 0,3m, L = 3m. The thickness m is calculated so that quantity of steel of isotropic piping is equal to one of corrugated piping, respectively.

Table 3.2 presents the effects of angle a and height  d on the elastic critical buckling load of corrugated piping with same steel quantity as isotropic piping, respectively. As can be seen, a very large effect of corrugation is obtained. The critical buckling load of corrugated piping is considerably greater than one of the same steel quantity isotropic piping. When angle a or height d increases, it is evident that critical buckling load increase.

Table 3.1. Comparison of the elastic critical buckling load of trapezoidal corrugated pipings of present results and Hieu et al.[10] (kN/m2)

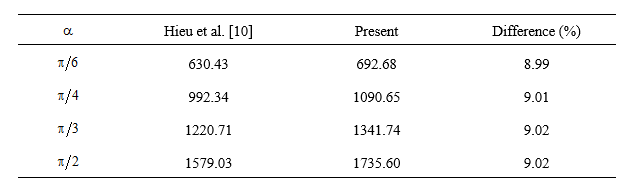Table 3.2. Effect of corugation on the critical buckling load of pipings (MN/m²)

 

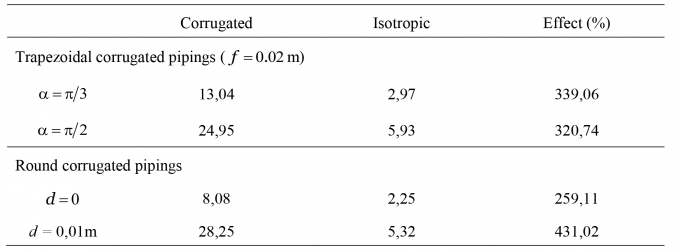Table 3.3. Effect of elastic foundation on the critical buckling load of pipings (MN/m²)

 

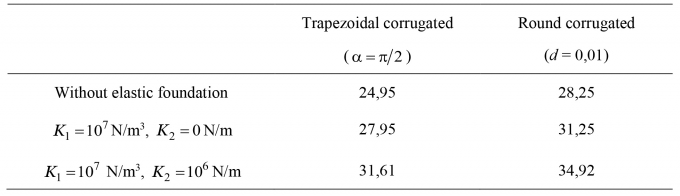Table 3.3 shows the effects of foundation parameters on the critical buckling load of pipings. Crearly, elastic foundation strongly influences on the critical buckling load, the critical buckling load of pipings with foundation is upper than one of without foundation pipings, respectively.

4. CONCLUSIONS

This paper presented an analytical approach of buckling analysis of corrugated piping. By using Donnell shell theory and a homogenization theory of corrugated structures, the governing equations of piping under external pressure and surrounded by elastic foundation were established. The critical buckling load was obtained in explicit form. The numerical results were compared with the same steel quantity isotropic pipings and estimated effect of elastic foundation on the critical buckling load of piping.

References

[1]. Xia, Y., Friswell, M.I., Saavedra Flores, E.I., (2012), Equivalent models of corrugated panels, International Journal of Solids and Structures 49, 1453-1462.

[2]. Samanta, A., Mukhopadhyay, M., (1999), Finite element static and dynamic analysis of folded plates, Eng. Struct. 21, 277-287.

[3]. Peng, L.X., Liew, K.M., Kitipornchai, S., (2007), Analysis of stiffened corrugated plates based on the FSDT via the mesh-free method, Int. J. of Mech. Sci. 49 (3), 364-378.

[4]. Yokozeki, T., Takeda, S.-I., Ogasawara, T., Ishikawa, T., (2006), Mechanical properties of corrugated composites for candidate materials of flexible wing structures, Compos. Part A 37, 1578-1586.

[5]. Kress, G., Winkler, M., (2010), Corrugated laminate homogenization model, Compos. Struct. 92 (3), 795-810.

[6]. Kress, G., Winkler, M., (2011), Corrugated laminate analysis: A generalized plane strain problem, Compos. Struct. 93 (5), 1493-1504.

[7]. Thill, C., Etches, J.A., Bond, I.P., Weaver, P.M., Potter, K.D., (2008), Experimental and parametric analysis of corrugated composite structures for morphing skin applications, In: 19th International Conference on Adaptive Structures Technology,Ascona, Switzerland.

[8]. Thill, C., Etches, J.A., Bond, I.P., Potter, K.D., Weaver, P.M., Wisnom, M.R., (2010), Investigation of trapezoidal corrugated aramid/epoxy laminates under large tensile displacements transverse to the corrugation direction, Compos. Part A - Applied Science and Manufacturing 41 (1), 168-176.

[9]. Winkler, M., Kress, G., (2010), Deformation limits for corrugated cross-ply laminates, Compos. Struct. 92 (6), 1458-1468.

[10]. Hieu, P.T., Nam, V.H., Phuong, N.T., Trang, L.T.N., Hung, V.T., (2016), Elastic stability of trapezoidal corrugated metal pipings subjected to external pressure, Internal journal of Science and Transport technology 1, 17-22.