Cơ sở lý thuyết nghiên cứu mô hình vật lý trong bể sóng 3D và máng sóng 2D

ª TS. Lê Quốc Tiến Trường Đại học Hàng hải Việt Nam Người phản biện: TS. Lê Thị Hương Giang TS. Trần Khánh Toàn

Tóm tắt:  Bài báo trình bày một cách tổng quát về cơ sở lý thuyết khi nghiên cứu thực nghiệm mô hình. Trong đó, tác giả trình bày rõ ràng các bước phân tích thứ nguyên của Pi-Buckingham để xác định mối quan hệ giữa các tham số chi phối độc lập cơ bản liên quan đến vấn đề nghiên cứu, làm cơ sở thiết kế và chế tạo mô hình cũng như đề xuất các chuỗi thí nghiệm mô hình vật lý thủy lực.

Từ khóa: Bể sóng 3D, máng sóng 2D.

Abstract: This paper presents generally about basis of theory in physical model investigation. In which, the author presents clearly four steps of Pi-Buckingham’s dimensional analysis to determine the relation among important independent variables concerning to research problem. This is the basis for designing and producing hydraulic  physical models.

Keywords: Wave pool 3D, 2D wave flume.

 1. Cơ sở lý luận về nghiên cứu mô hình vật lý

Cơ sở lý luận để thí nghiệm mô hình vật lý là dựa vào lý thuyết tương tự mô hình. Mô hình thu nhỏ được xây dựng để mô phỏng các quá trình vật lý và hiện tượng một cách tương tự như trong điều kiện nguyên mẫu. Thí nghiệm mô hình được sử dụng để dự báo các tham số thiết kế sẽ xảy ra với mô hình nguyên mẫu trong phạm vi giới hạn của điều kiện thí nghiệm.

Tương tự mô hình được xây dựng chủ yếu dựa vào phép phân tích thứ nguyên.

Thứ nguyên là một khái niệm dùng để phân biệt các chủng loại của đại lượng vật lý, được diễn đạt bằng một ký hiệu đơn giản (chữ cái) và đóng mở bằng một ngoặc vuông ([]). Có 2 loại thứ nguyên:

- Thứ nguyên cơ bản: Thứ nguyên không thể thay thế bằng thứ nguyên khác. Ví dụ: Độ dài [L], khối lượng [M], thời gian [T], nhiệt độ [º], góc [rad].

- Thứ nguyên dẫn xuất: Thứ nguyên của đại lượng vật lý dẫn xuất. Ví dụ: Diện tích [L²], khối lượng riêng [ML^-3]…

Tỷ số giữa hai đại lượng vật lý giống nhau dẫn đến một đại lượng vật lý không thứ nguyên gọi là đại lượng không thứ nguyên.

Phân tích thứ nguyênlà phương pháp mà nhờ nó chúng ta có thể nắm được những kiến thức cơ bản về hiện tượng thủy lực cần nghiên cứu, tìm ra chuẩn tắc tương tự mô hình, dùng để hiệu chỉnh các công thức, hoán đổi đơn vị, chỉ đạo tổ chức thí nghiệm, giảm thiểu các biến số trong phân tích số liệu thực nghiệm. Cơ sở lý luận của phương pháp là một phương trình vật lý đúng phải là một phương trình đồng nhất về thứ nguyên.

Năm 1914, Buckingham đưa ra định lý tổng quát về phép phân tích thứ nguyên, đó là định luật Pi (P) nổi tiếng như sau:

Giả sử vấn đề nghiên cứu có n đại lượng biến đổi độc lập, theo lý thuyết Buckingham thì có thể biểu diễn các đại lượng biến đổi a₁, a₂, a₃... a_n, mô tả hiện tượng thủy động lực học cần nghiên cứu trong một phiếm hàm:

f(a₁, a₂, a₃, …, a_n) = 0                   (1)

Quan hệ (1) có thể biểu diễn dưới một dạng khác của các biến không thứ nguyên P₁, P₂, P₃,…, P_i  với P₁, P₂, P₃..., P_i  được thiết lập từ các đại luợng a₁, a₂, a₃..., a_n. Tổng số các biến không thứ nguyên sẽ ít hơn tổng số các đại lượng vật lý biến đổi. Nghĩa là chúng ta có một phiến hàm khác:

f(P₁, P₂, P₃...., P_n-r ) = 0                  (2)

Trong đó:

- P_j - Các biến không thứ nguyên; j = 1 ¸ (n-r);

- r - Các đại lượng (số biến) cơ bản, chúng ta chọn số thứ nguyên cơ bản tối đa (r £ 3) (cả hình học, động học, động lực học);

- n - Các đại lượng biến đổi độc lập được chọn ở (1).

Các bước thực hiện phân tích thứ nguyên

Bước 1: Nhận dạng được những tham số cơ bản chi phối quá trình vật lý xem xét (k tham số). Yêu cầu cần nắm rõ quy luật chi phối của quá trình vật lý để chỉ đưa ra những tham số quan trọng về hình học, vật liệu, môi trường (tác động). Các tham số này phải độc lập với nhau. Nếu quá nhiều (thừa) sẽ làm cho vấn đề nghiên cứu phức tạp hóa không cần thiết, nếu quá ít (thiếu) dẫn đến kết quả nghiên cứu không tin cậy.

Bước 2: Biểu diễn thứ nguyên của từng tham số dưới dạng các thứ nguyên cơ bản. Ví dụ: Độ sâu nước D [L]; chiều cao sóng H [L]; chu kì sóng T [T]; khối lượng riêng ρ [M^-3], sau đó xác định số thứ nguyên cơ bản r của bài toán với hầu hết các quá trình thủy động lực học r = 3.

Bước 3: Xác định số các đại lượng phi thứ nguyên P_i = (k – r ).

Bước 4: Xây dựng (k – r ) các đại lượng phi thứ nguyên  P_i. Sử dụng phép thử thứ nguyên và kiến thức về vấn đề xem xét để xây dựng các P_i. Bao gồm:

- Kết hợp giữa các biến số độc lập để hình thành các P_i (lưu ý không thứ nguyên);

- Mỗi một biến độc lập phải xuất hiện ít nhất 01 lần trong các P_i;

- Cố gắng lý giải ý nghĩa vật lý của các các P_i;

- Tìm các liên hệ/ràng buộc vật lý giữa các P_i.

2. Yêu cầu về tương tự mô hình

2.1. Tỉ lệ mô hình

Là tỉ lệ giá trị của một tham số ở nguyên mẫu và trong mô hình. Gọi tham số là X, ta có:   N_x = X_y / X_m        ;

- Tỉ lệ chiều dài:     N_L = N_P / N_m         ;

- Tỉ lệ diện tích: N_A=N_L²;

- Tỉ lệ lưu tốc:  N_v = N_L / N_t            ;

N_t  được rút ra theo tiêu chuẩn tương tự yêu cầu.

Bảng 2.1. Tỉ lệ của một số đại lượng vật lý cơ bản theo tiêu chuẩn tương tự Froude

 

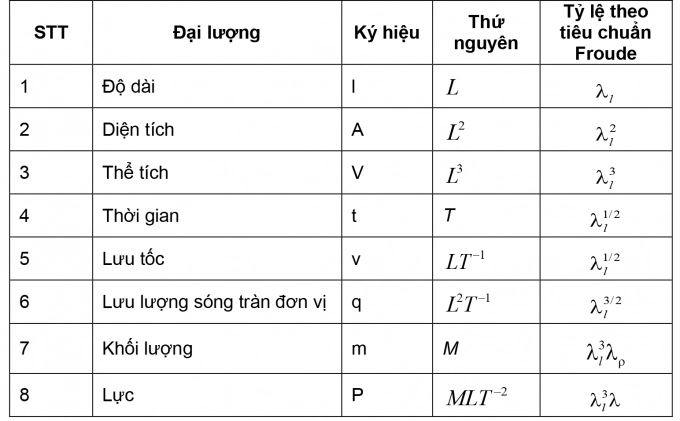2.2. Tính đồng dạng mô hình

Để có được tỉ lệ mô hình phù hợp cần dựa vào tính đồng dạng giữa mô hình và nguyên mẫu. Trong cơ học chất lỏng, nói chung có ba loại đồng dạng cơ bản:

- Đồng dạng hình học: Tỉ lệ hình học giữa tất cả các kích thước cạnh là như nhau. Với mô hình không biến dạng hay mô hình chính thái (tỉ lệ theo phương ngang và phương đứng như nhau) chỉ có một giá trị hằng số tỉ lệ N_L.

- Đồng dạng động học: Đồng dạng về chuyển động của các hạt giữa mô hình và nguyên mẫu.

- Đồng dạng động lực học: Là sự đồng dạng của lực tác dụng giữa mô hình và nguyên mẫu nhằm đảm bảo tỉ lệ như nhau của các véc-tơ lực giữa mô hình và nguyên mẫu.

Đối với chuyển động của sóng, dòng chảy thông thường có các lực trọng trường, lực áp suất, lực nhớt, lực căng mặt ngoài, lực quán tính. Để có được đồng dạng động lực học hoàn hảo thì các lực này phải song song với nhau tại các điểm tương ứng giữa mô hình và nguyên mẫu và có cùng một tỉ lệ (đồng dạng cả về hướng và độ lớn). Tuy nhiên, trong thực tế, những lực này không phải đồng thời tồn tại ở cả mô hình và nguyên mẫu. Đặc biệt với mô hình thu nhỏ thì đồng dạng này không bao giờ thỏa mãn mà chỉ xác định các tỉ lệ lực quan trọng cần thỏa mãn theo tiêu chuẩn tương tự được lựa chọn phù hợp với mô hình nghiên cứu để cân bằng giữa yêu cầu về độ chính xác và tính đơn giản của mô hình.

2.3. Các tiêu chuẩn tương tự thủy lực

2.3.1. Tiêu chuẩn Froude

Thể hiện sự tương quan tương đối giữa lực quán tính và lực trọng trường (mức độ quan trọng tương đối giữa lực quán tính tác động lên hạt chuyển động và trọng lượng bản thân của hạt).

 

       

                                 

 

 

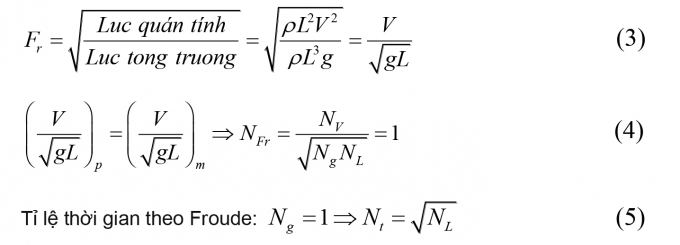Tiêu chuẩn Froude áp dụng cho các dòng chảy có mặt thoáng trong tự nhiên (dòng chảy có lực quán tính được cân bằng bởi các lực trọng trường).

2.3.2. Tiêu chuẩn Reynolds

Thể hiện mức độ quan trọng tương đối giữa lực quán tính và lực nhớt tác động lên hạt chuyển động.

 

 

 

 

 

 

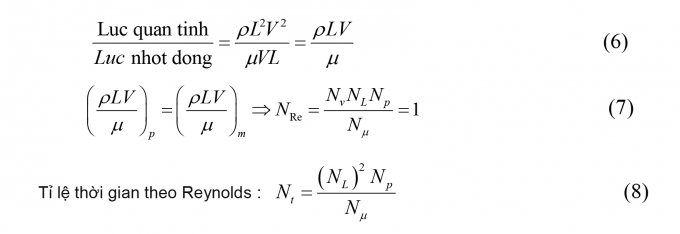Tiêu chuẩn Reynolds mô phỏng dòng chảy có lực nhớt chiếm ưu thế: Dòng chảy tầng ở lớp biên, lực tác động lên tuốc bin thủy lực.

Trên đây là hai tiêu chuẩn tương tự quan trọng bậc nhất cho hầu hết các mô hình thủy lực. Căn cứ vào phạm vi áp dụng của hai tiêu chuẩn và nội dung của vấn đề nghiên cứu để lựa chọn thiết kế mô hình thí nghiệm theo tiêu chuẩn tương tự phù hợp.

4. Kết luận và kiến nghị

Tác giả đã trình bày cơ sở lý thuyết trong nghiên cứu thiết kế và chế tạo các mô hình thí nghiệm thủy lực, trong đó đưa ra các bước cụ thể áp dụng phép phân tích thứ nguyên của Buckingham để xác định mối quan hệ giữa các tham số chi phối của vấn đề nghiên cứu, làm cơ sở đề xuất các chuỗi thí nghiệm mô hình vật lý.

Tài liệu tham khảo

[1]. Thiều Quang Tuấn, bài giảng: Giới thiệu kỹ thuật ngành nghiên cứu mô hình vật lý máng sóng, Trường Đại học Thủy Lợi.

[2]. Trường Đại học Thủy Lợi (1998), Giáo trình Thủy lực, Hà Nội.

[3]. Phạm Ngọc Quý, bài giảng: Thực nghiệm mô hình thủy lực công trình thủy lợi, Trường Đại học Thủy Lợi.

[4]. Battjes, J.A. and Janssen, J.P.F.M. (1978), Energy loss and set-up due to breaking of random waves, Proc. 14th Int. Conf. Coastal Engineering, ASCE, pp. 466-480.

[5]. Battjes, J.A. and Janssen, T.T. (2008), Random wave breaking models: History and discussion, In Proc. 31th Int. Conf. Coastal Engineering, Hamburg, Germany.

[6]. Hughes, A.S. (ed.) (1993), Physical models and laboratory techniques in coastal engineering, World Scientific, Singapore, 568 pp.

[7]. TAW (2002), Technical report wave run-up and wave overtopping at dikes, Technical Advisory Committee on Flood Defence, The Netherlands.

[8]. Van Gent, M.R.A. (2001), Wave runup on dikes with shallow foreshores, J. Waterw. Port Coastal Ocean Eng., ASCE, 127, 5, pp. 254-262.