Đánh giá khả năng sử dụng phần mềm Plaxis trong phân tích ổn định nền đường sắt

TÓM TẮT: Hiện nay, trong các tiêu chuẩn thiết kế, giá trị hệ số ổn định cho phép của nền đường giao thông nói chung và nền đường sắt nói riêng được xây dựng trên cơ sở phương pháp cân bằng giới hạn (CBGH). Gần đây, Plaxis cũng là một phần mềm đang được sử dụng rất phổ biến trong tính toán ổn định mái dốc, nhưng lại dựa trên lý thuyết khác hoàn toàn với CBGH. Bài báo giới thiệu những phân tích so sánh hệ số ổn định xác định bằng Plaxis với hệ số ổn định xác định bằng phương pháp CBGH để đánh giá khả năng sử dụng phần mềm Plaxis trong phân tích ổn định mái dốc nền đường sắt.

Từ khóa: Phân tích ổn định nền đường sắt, hệ số ổn định cho phép, phương pháp cân bằng giới hạn, phần mềm Plaxis.

ABSTRACT: In the design standards at present, allowable factor of safety of the embankment in general and the railway embankment in particular is built on the basis of the limit equilibrium method. Recently, Plaxis is also a very popular software used in slope stabilization, but it is based on a completely different theory of limit equilibrium. The article presents comparative analysis of the factor of safety determined by Plaxis with the factor of safety determined by the limit equilibrium method to evaluate the ability to use Plaxis software in analyzing stability of slope of railway embankment.

Keywords: Analyzing stability of slope of railway embankment, allowable factor of safety, limit equilibrium method, plaxis software.

1. ĐẶT VẤN ĐỀTừ trước đến nay, việc tính toán ổn định nền đường giao thông nói chung và nền đường sắt nói riêng thường dựa trên cơ sở lý thuyết của phương pháp CBGH để đánh giá mức độ ổn định của nền đường thông qua hệ số ổn định K. “Cân bằng giới hạn” ở đây được hiểu là sự cân bằng giữa mô-men giữ với mô-men gây trượt, hay giữa lực giữ với lực gây trượt. Việc tính toán có thể được tính toán một cách thủ công hoặc sử dụng các phần mềm máy tính, trong đó phổ biến nhất là phần mềm tính ổn định mái dốc “Slope/W”.Tuy nhiên, gần đây một phần mềm máy tính cũng đang bước đầu được sử dụng phổ biến trong các bài toán địa kỹ thuật đó là phần mềm Plaxis, do tính chính xác và khả năng giải quyết bài toán rất rộng của nó. Đối với bài toán ổn định mái dốc, phần mềm Plaxis dựa trên cơ sở lý thuyết hoàn toàn mới, đó là phương pháp suy giảm cường độ chống cắt để xác định hệ số ổn định nền móng.Việc nghiên cứu và sử dụng cả hai phương pháp này cho cùng một bài toán ổn định nền đường sẽ giúp cho việc phân tích đánh giá ổn định nền đường được khách quan hơn và đặc biệt là sẽ giúp cho người thiết kế lựa chọn phương pháp phân tích ổn định nền đường sắt phù hợp và có độ tin cậy nhất.
2.TÍNH TOÁN ỔN ĐỊNH MÁI DỐC THEO PHƯƠNG PHÁP CBGH2.1. Cơ sở lý thuyết của phương pháp CBGH- Trọng lượng khối trượt W sẽ gây nên một mô-men lực (nếu là mặt trượt cung tròn) hay lực (nếu là mặt trượt phẳng) làm cho khối đất bị trượt;- Lực ma sát và lực dính sẽ gây nên một mô-men hoặc lực ngược chiều hướng dịch chuyển làm khối đất ổn định;- Khối đất trượt được chia thành các mảnh nhỏ có kích thước tùy ý, các mô-men (hay lực) gây trượt và mô-men (lực) giữ ổn định của khối đất sẽ bằng tổng các mô-men (lực) của các mảnh.Hình 2.1: Lực tác dụng lên mặt trượt thông qua khối trượt với mặt trượt trònHệ số ổn định của mái dốc có thể được xác định từ điều kiện cân bằng mô-men hoặc cân bằng lực hoặc điều kiện cân bằng giới hạn tổng quát.2.2. Sử dụng phần mềm Slope/W tính toán ổn định mái dốcChương trình SLOPE/W được xây dựng dựa trên một số lý thuyết tính ổn định mái dốc như: Phương pháp Ordinary (hay còn gọi là phương pháp Fellenius), phương pháp Bishop, phương pháp Janbu, phương pháp Spencer, phương pháp Morgen-price, phương pháp cân bằng tổng quát G.L.E... Đặc điểm khác biệt cơ bản giữa các phương pháp khác nhau là giả thiết liên quan đến lực tiếp tuyến và pháp tuyến giữa các dải. Hơn nữa, rất nhiều hàm số biểu diễn quan hệ giữa các lực tác động giữa các cạnh của các dải cũng được sử dụng đối với các phương pháp G.L.E và phương pháp Morgenstern-price mà các phương pháp này rất chặt chẽ về mặt toán học. SLOPE/W đưa ra rất nhiều các phương pháp tính toán khác nhau để cho người dùng có thể lựa chọn phương pháp phù hợp nhất với bài toán của mình.- Các phương pháp Morgenstern-Price, Spencer và G.L.E thỏa mãn cả hai điều kiện cân bằng lực và cân bằng mô-men, do vậy tính chính xác cao. - Phương pháp Ordinary do đã bỏ qua lực pháp tuyến và lực cắt giữa các mảnh trượt nên tính chính xác không cao, do vậy ít được sử dụng trong thực tế. - Phương pháp Janbu tính theo điều kiện cân bằng lực gây xoắn vặn các thỏi đất gây ảnh hưởng nhiều tới lực cắt giữa các thỏi, nên phương pháp này cho kết quả sai khác nhiều so với phương pháp Morgenstern-Price và G.L.E. - Phương pháp Bishop tính do theo điều kiện cân bằng mô-men ít gây xoắn vặn các thỏi đất, nên ít ảnh hưởng tới lực cắt giữa các thỏi, do vậy phương pháp này cho kết quả không sai khác nhiều so với phương pháp Morgenstern-Price và G.L.E. Do vậy, hiện nay phương pháp Bishop thường được dùng trong tính toán ổn định nền đường.Theo qui định trong “Qui trình khảo sát thiết kế nền đường ô tô đắp trên nền đất yếu” 22TCN262-2000, khi áp dụng phương pháp kinh nghiệm kiểm toán ổn định theo các cách phân mảnh cổ điển với mặt trượt tròn, hệ số ổn định nhỏ nhất [K] = 1.2. Khi sử dụng phương pháp Bishop để tính toán ổn định thì hệ số ổn định cho phép sẽ lấy là [K] = 1.4.Từ các phân tích trên, hiện nay phương pháp được dùng để kiểm toán ổn định nền đường và ta-luy thông dụng nhất và cho kết qủa khá chính xác là phương pháp Bishop.
3. LÝ THUYẾT TÍNH TOÁN ỔN ĐỊNH MÁI DỐC THEO PHƯƠNG PHÁP SUY GIẢM CƯỜNG ĐỘ TRONGPHẦN MỀM PLAXISSuy giảm cường độ phi-C là một lựa chọn sẵn có trong Plaxis để tính toán hệ số ổn định của công trình. Lựa chọn này là một dạng tính toán riêng trong General tab sheet. Trong phương pháp Phi-C reduction, tham số độ bền φ và c của đất được cho giảm liên tục cho đến khi xuất hiện sự phá hoại của kết cấu. Độ bền của các mặt tiếp xúc nếu được đưa vào tính toán cũng được giảm theo cách này. Độ bền của các kết cấu dạng tấm bản và neo là không bị ảnh hưởng khi cho giảm Phi-C của đất.Tổng bội số SMsf được sử dụng để xác định giá trị các tham số độ bền của đất tại một giai đoạn phân tích xác định:

Ở đây, các tham số độ bền với chỉ số dưới “input” là các tham số đầu vào trong phần nhập số liệu và các tham số chỉ số dưới “reduced” là các giá trị bị giảm dần trong quá trình phân tích. SMsf được gán từ giá trị 1.0 tại thời điểm bắt đầu tính toán và thay đổi cho tới giá trị mà độ bền của tất cả các vật liệu không thể giảm được nữa.Quá trình tính toán Phi-c reduction được thực hiện qua việc sử dụng thủ tục Load advanceement number of steps. Số gia Msf (bước tăng của Msf ) được gán trước và nó thể hiện số gia của sự suy giảm độ bền so với bước tính toán đầu tiên. Số gia này được mặc định là 0.1 (mỗi lần thay đổi có giá trị là 0.1). Tham số độ bền được giảm liên tục một cách tự động cho đến khi tổng số bước tính toán qui định trước được thực hiện hết. Nó phải luôn được kiểm tra xem bước tính cuối cùng có thể dẫn đến cơ chế phá hoại được diễn ra đầy đủ hay không. Nếu rơi vào trường hợp này thì hệ số ổn định là:

Nếu cơ chế phá hoại không được phát triển đầy đủ thì việc tính toán phải được lặp với số lượng bước tính toán lớn hơn.
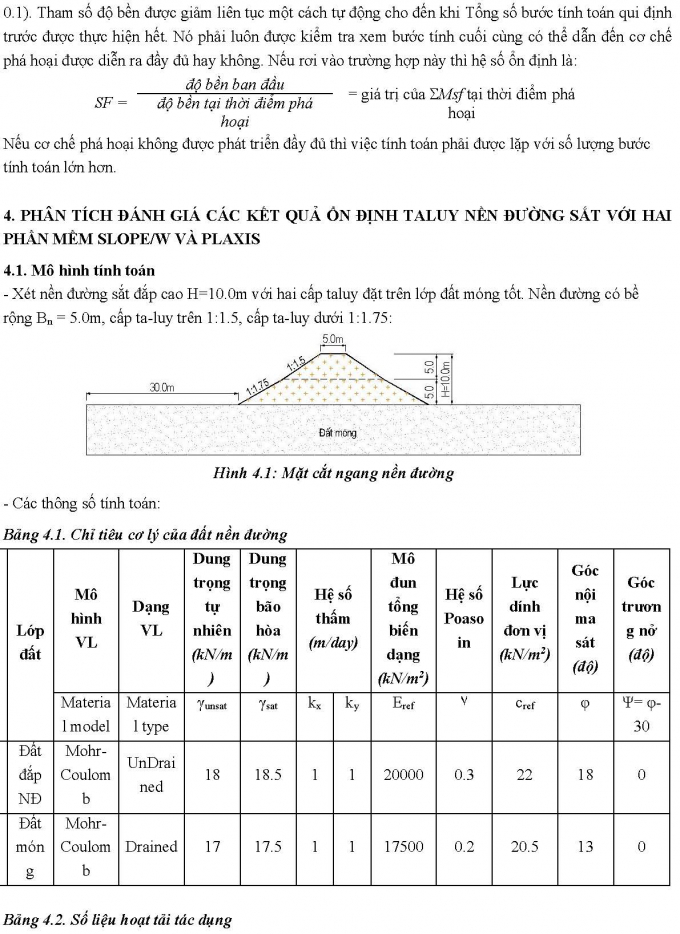
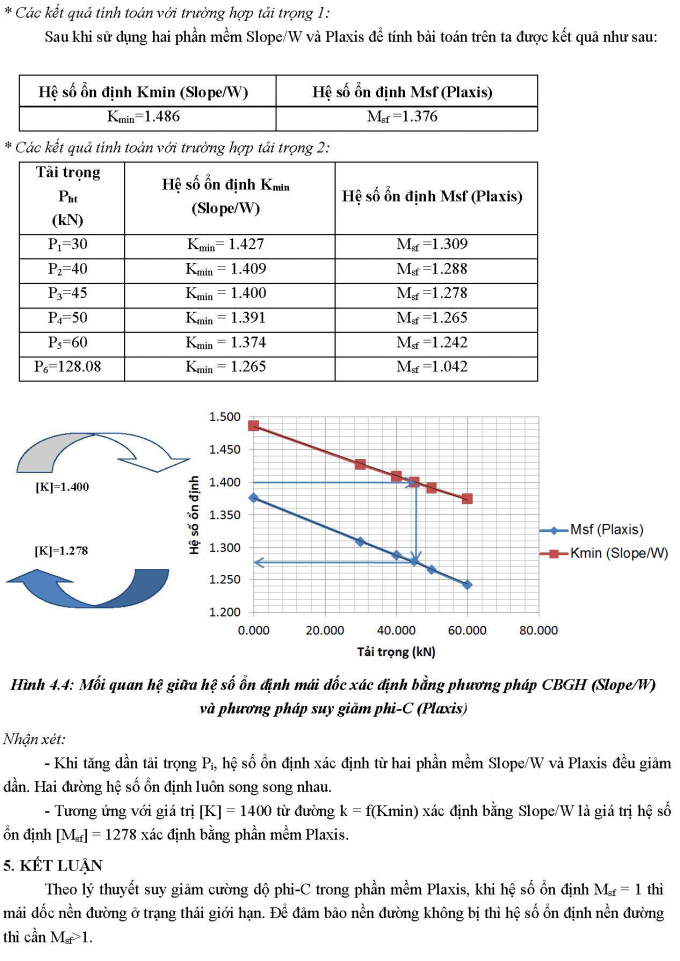
4. PHÂN TÍCH ĐÁNH GIÁ CÁC KẾT QUẢ ỔN ĐỊNH TA-LUY NỀN ĐƯỜNG SẮT VỚI HAI PHẦN MỀM SLOPE/W VÀ PLAXIS4.1. Mô hình tính toán- Xét nền đường sắt đắp cao H = 10.0m với hai cấp ta-luy đặt trên lớp đất móng tốt. Nền đường có bề rộng Bn  = 5.0m, cấp ta-luy trên 1:1.5, cấp ta-luy dưới 1:1.75:Hình 4.1: Mặt cắt ngang nền đường- Các thông số tính toán:Bảng 4.1. Chỉ tiêu cơ lý của đất nền đườngBảng 4.2. Số liệu hoạt tải tác dụng4.2. Kết quả tính toán4.2.1. Các trường hợp tính toán- Trường hợp 1: Tính hệ số ổn định nền đường khi chưa có hoạt tải, khi đó chỉ có tải trọng bản thân của nền đắp và tải trọng của kết cấu tầng trên.- Trường hợp 2: Tính hệ số ổn định nền đường khi xét thêm tải trọng đoàn tàu. 4.2.2. Các kết quả tính toán hệ số ổn định nền đườngHình 4.2: Dạng cung tròn nguy hiểm nhất xác định bằng Slope/WHình 4.3: Dạng cung tròn nguy hiểm nhất xác định bằng Plaxis* Các kết quả tính toán với trường hợp tải trọng 1:Sau khi sử dụng hai phần mềm Slope/W và Plaxis để tính bài toán trên ta được kết quả như sau:* Các kết quả tính toán với trường hợp tải trọng 2:Hình 4.4: Mối quan hệ giữa hệ số ổn định mái dốc xác định bằng phương pháp CBGH (Slope/W) và phương pháp suy giảm phi-C (Plaxis)Nhận xét:- Khi tăng dần tải trọng Pi, hệ số ổn định xác định từ hai phần mềm Slope/W và Plaxis đều giảm dần. Hai đường hệ số ổn định luôn song song nhau.- Tương ứng với giá trị [K] = 1400 từ đường k = f(Kmin) xác định bằng Slope/W là giá trị hệ số ổn định [Msf] = 1278 xác định bằng phần mềm Plaxis.
5. KẾT LUẬNTheo lý thuyết suy giảm cường độ phi-C trong phần mềm Plaxis, khi hệ số ổn định Msf = 1 thì mái dốc nền đường ở trạng thái giới hạn. Để đảm bảo nền đường không bị thì hệ số ổn định nền đường thì cần Msf>1.Mức độ tin cậy của phần mềm Plaxis có thể cao hơn phần mềm Slope/W do trong phần mềm xét đến nhiều thông số địa kỹ thuật hơn Slope/W. Do chưa có một quy định nào về hệ số ổn định cho phép của mái dốc khi tính theo phương pháp suy giảm cường độ phi-C (Plaxis), qua kết quả nghiên cứu ở trên có thể tạm lấy hệ số ổn định mái dốc cho phép khi tính bằng Plaxis là [Msf] = 1.28 - 1.30, tương ứng với hệ số [K]=1.40 khi xác định bằng phương pháp CBGH o
Tài liệu tham khảo[1]. PGS. TS. Nguyễn Thanh Tùng, KS. Lê Văn Cử, ThS. Bùi Thị Trí (2004), Nền đường sắt, NXB. GTVT, Hà Nội.[2]. PGS. TS. Bùi Anh Định (2004), Cơ học đất, NXB. GTVT, Hà Nội.[3]. Quy trình khảo sát thiết kế nền đường ô tô đắp trên đất yếu 22TCN 262-2000.