Điều khiển cánh tay robot hai bậc tự do qua mạng dựa trên phương pháp dự đoán Smith nâng cao

TS. Đặng Xuân Kiên; KS. Nguyễn Mạnh La Trường Đại học Giao thông vận tải TP. Hồ Chí Minh Người phản biện: TS Võ Công Phương

TÓM TẮT: Bài báo nghiên cứu thiết kế mô hình điều khiển cánh tay máy hai bậc tự do qua mạng dựa vào phương pháp dự đoán Smith nâng cao. Trễ điều khiển gây ra bởi tính chất mạng và đáp ứng trễ của cơ cấu chấp hành, dẫn tới tín hiệu điều khiển cánh tay robot bị chậm, rất khó đạt được độ ổn định khi điều khiển qua mạng. Phương pháp dự đoán Smith nâng cao giúp dự đoán tương đối tín hiệu trễ của toàn hệ thống làm tăng khả năng thích nghi với ảnh hưởng của thời gian trễ, giúp tay máy đáp ứng chính xác.

TỪ KHÓA: Dự đoán Smith, cánh tay máy, điều khiển qua mạng.

Abstract: In this paper, our study is based on advanced Smith predictor to design the networked control system of two links flexible robot arm. Controlled time-delays depend on the delays of network and the delays of actuator responses, so it is difficult to obtain the stable and accurate control. The advanced Smith predictor is an adaptive predict method, the system is capable of adapting to the effects of time delay to in getting a better of accuracy of networked control system.

Keywords: Smith predictor, two-link flexible robot arm, networked control system.

1. ĐẶT VẤN ĐỀ

Hiện nay, các công trình nghiên cứu về robot rất đa dạng đem lại nhiều ứng dụng cụ thể trong đời sống, trong công nghiệp và quân sự. Việc điều khiển robot qua mạng đã được nhiều nhà nghiên cứu quan tâm ở rất nhiều khía cạnh. Trong phạm vi của bài báo, các tác giả đề cập tới việc điều khiển bù thích nghi thời gian trễ trong điều khiển cánh tay máy hai bậc tự do qua mạng. Nhiều nhà thiết kế đã đưa mô hình hệ thống điều khiển nâng cao có kèm theo bộ dự báo Smith tạo ra từ nhận dạng neuron, bằng cách đó thì dù thời gian trễ có lớn hơn nhiều hệ thống vẫn giữ được ổn định.

Đối tượng mô phỏng trong bài báo là một hệ thống cánh tay máy hai bậc tự do [1]. Việc nhận dạng đối với các đối tượng thực tế thông qua mạng neuron đã được nghiên cứu [2-4] và đã áp dụng thành công. Mạng neuron cũng được sử dụng để thiết lập đối tượng giả lập trong bộ dự báo Smith [5-6], kết quả cho thấy hệ thống đáp ứng tốt. Về kỹ thuật điều khiển, các giải thuật điều khiển cánh tay máy hai bậc đã được thử nghiệm thành công như PID, điều khiển mờ, điều khiển thích nghi  và điều khiển trượt, nhưng khi sử dụng các giải thuật này để áp dụng điều khiển các đối tượng phức tạp thì chưa được kiểm chứng khả năng và đáp ứng của chúng. Bài báo trình bày tập trung việc điều khiển cánh tay máy hai bậc là đối tượng điều khiển nhiều vào - nhiều ra (MIMO) điển hình thông qua mạng điều khiển, lựa chọn bộ điều khiển PID nhằm đơn giản hóa việc thiết kế và điều chỉnh thông số.

2. CÁNH TAY HAI BẬC TỰ DO

Cánh tay máy hai bậc tự do gồm hai khớp (link) link 1 và link 2 được điều khiển để ở đúng vị trí xác định trong mặt phẳng không gian, mô tả trên Hình 2.1:

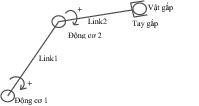Hình 2.1: Cánh tay máy hai bậc tự do

 

 

 

Hệ cánh tay máy xét ở đây là hệ MIMO hai vào hai ra được mô tả như trong tài liệu [1].

3. XÂY DỰNG MÔ HÌNH SMITH-PREDICTOR

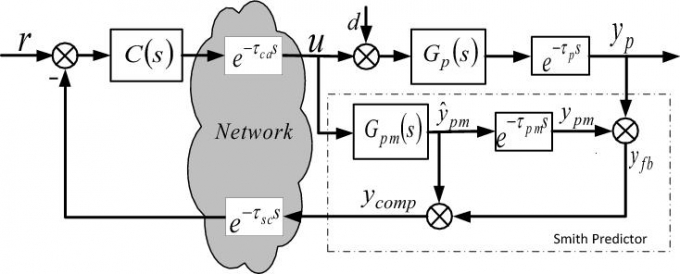Hình 3.1: Cấu trúc hệ thống dựa trên mô hình dự báo Smith

 

 

 

 

 

 

 

 

 

4. ỨNG DỤNG MẠNG NEURON TRONG NHẬN DẠNG ĐỐI TƯỢNG THỰC TẾ

Để nhận dạng hệ thống động dùng mạng truyền thẳng nhiều lớp (Multi Layer Perceptron-MLP) [3], bộ dự báo có sơ đồ khối như trình bày ở Hình 4.1, trong đó các tế bào ở lớp ẩn với hàm tác động là hàm Sigmoid, một tế bào ở lớp ra với hàm tác động tuyến tính. Chọn thời gian lấy mẫu là 0.1s. Cho hệ thống chạy huấn luyện mạng trong tối đa 5.000s với các tín hiệu vào ngẫu nhiên: Tau1, tau2, teta1_dot_init, teta1_dot, teta2_init,  teta2_dot_init.

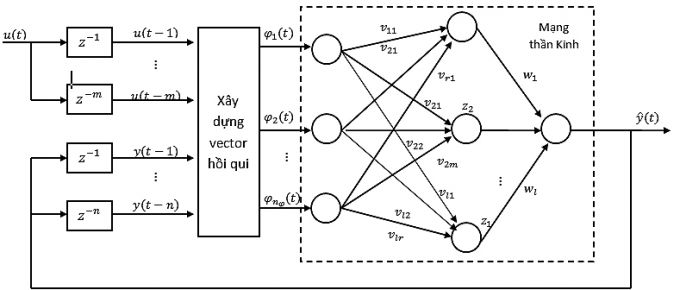Hình 4.1: Mô hình xây dựng khối neuron

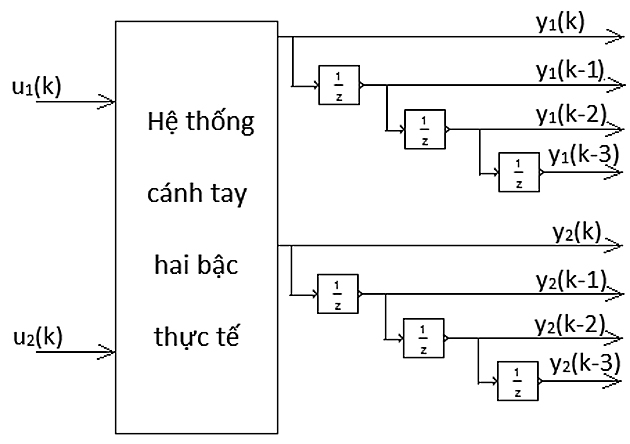
Sơ đồ khối neuron vào-ra mô tả trên Hình 4.2 như sau: Từ tín hiệu ngõ vào u1(k) và u2(k) như trên, ta tiến hành thu thập các tín hiệu và sử dụng phương pháp nhận dạng lan truyền ngược để nhận dạng y1(k-1), y1(k-2), y1(k-3), y2(k-1), y2(k-2), y2(k-3) như sau:

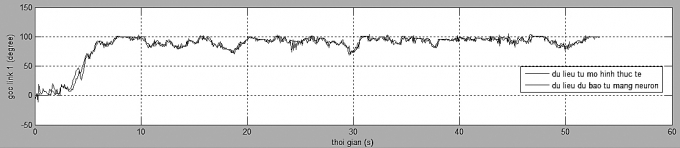
Kết quả nhận dạng và đáp ứng thực tế thể hiện trên Hình 4.4 cho thấy, hệ thống nhận dạng bám sát với đối tượng thực, tuy vẫn còn sai số nhưng chấp nhận được.

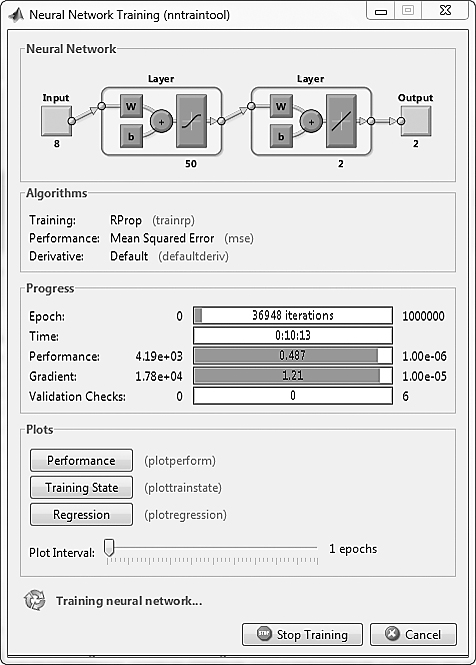Hình 4.3: Nhận dạng dùng mạng neuron

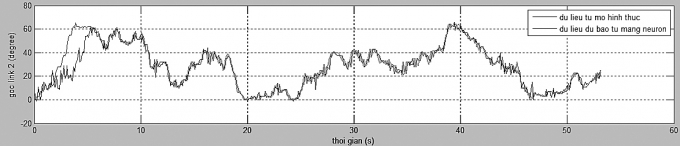Hình 4.4: So sánh giữa tín hiệu thực tế ngõ ra hệ thống và mạng neuron thu được

5. MÔ PHỎNG 

5.1. Cài đặt thông số

* Thông số bộ điều khiển PID được khảo sát bằng PIDtool trên Matlab:

- Kp1= 974,79; Ki1= 91,83;  Kd1= 81,38.

- Kp2= 545,21; Ki2= 70,69;  Kd2 = 83,99.

* Thông số mô hình:

- Jmin = 67,4901; J1=5; J2=5.

- m1=1; m2=1; m3=0.1; l1=1; l2=1;lc1=0,4; lc2=0,4; g=9.81; teta1_init=pi/2; teta1_dot_init=0; teta2_init=0; teta2_dot_init=0; delta_t=0,01.

* Chọn giá trị khởi tạo ban đầu:

Teta1 có giá trị đặt là pi/2 (rad) tức 2,1 (rad); teta2 có giá trị đặt là pi/9 (rad) tức 0,32 (rad).

5.2. Mô phỏng quá trình điều khiển trong 2 trường hợp

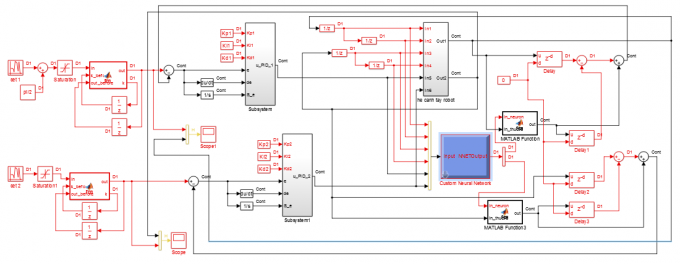Hình 5.1: Sơ đồ hệ thống điều khiển

Sơ đồ điều khiển Hình 5.1 xây dựng trên Matlab Simulink, kết quả mô phỏng với 2 trường hợp nhận dạng có trễ (Hình 5.2) và không có trễ (Hình 5.3):

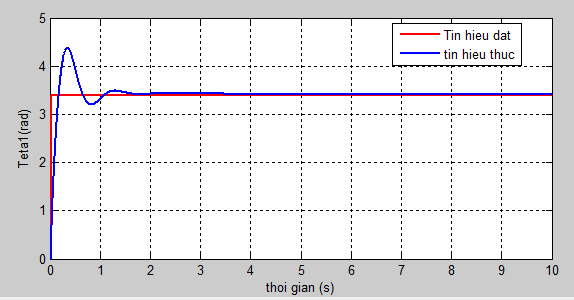Hình 5.2: Teta1 khi nhận dạng có trễ

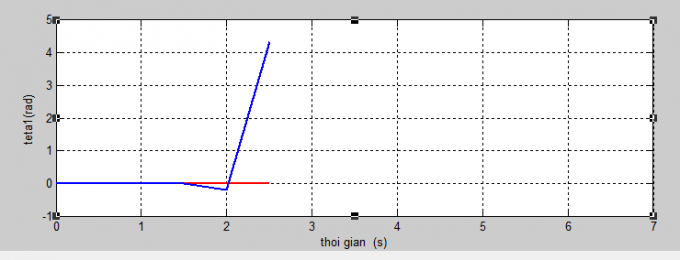Hình 5.3: Teta1 khi nhận dạng không trễ

Nhận xét: Trường hợp nhận dạng cánh tay không có trễ, khi mô phỏng thực hệ thống mất ổn định. Trường hợp bộ nhận dạng nơ ron với cánh tay điều khiển có trễ, mô hình Smith lúc này phát huy tác dụng và đáp ứng đầu ra đạt được sự ổn định. Kết quả tương tự với góc Teta2.

6. KẾT LUẬN

Từ các kết quả mô phỏng cho thấy, cấu trúc điều khiển Smith ứng dụng bộ nhận dạng neuron cho đáp ứng tốt. Tuy nhiên, thời gian trễ vẫn còn phải được giả lập bên trong lập trình, thời gian trễ do tính chất mạng thay đổi không định trước vẫn chưa có biện pháp khắc phục được hoàn toàn. Việc xây dựng mô hình thực nghiệm đã kiểm chứng những lý thuyết nêu trên và sẽ được trình bày ở những bài báo tiếp theo.

Tài liệu tham khảo

[1]. K. Yamada, Y. Ando, T. Hagiwara, I Murakami, N T Mai (2009), A Design Method for 2-Degree-Of-Freedom Modified Smith Predictors, Proc of the Fourth International Conference on Innovative Computing, Information and Control, pp 152-155.

[2]. A. Vodencarevic (2010), Design of PLC-based Smith Predictor for Controlling Processes with Long Dead Time, Proceedings of the International MultiConference of Engineers and Computer Scientists, Vol II.

[3]. Narendra, K.S, Parthasarathy, K. (1990), Identification and control of dynamical systems using neural networks,  IEEE Trans on Neural Networks, Vol 1. 

[4]. X. K. Dang, Z. H. Guan, H. D. Tran and T. Li (Jul 2011), Fuzzy Adaptive Control of Networked Control System with Unknown Time-delay, Proc. The 30th Chinese Control Conference, Yan tai, China, pp. 4622 - 4626.

[5]. X. K. Dang, Z. H. Guan, T. Li and D. X. Zhang (2012), Joint Smith Predictor and Neural Network Estimation Scheme for Compensating Randomly Varying Time-delay in Networked Control System, Proc, The 24th Chinese Control and Decision Conference, Tai Yuan, China, May.

[6]. X.K. Dang, V.T. Nguyen, X. P. Nguyen (Dec 2015), Robust Control of Networked Control Systems with Randomly Varying Time-Delays Based Adaptive Smith Predictor, Rangsit Journal of Arts and Sciences, Vol. 5, pp.175-186.