Điều khiển robot tự hành bằng phương pháp điều khiển hành vi dựa trên không gian rỗng

ThS. Lê Thị Thúy Nga TS. Nguyễn Hoàng Vân KS. Nguyễn Việt Dũng Trường Đại học Giao thông vận tải Người phản biện: TS. Lại Mạnh Dũng TS. Nguyễn Văn Tiềm

Tóm tắt: Bài báo đã phát triển một mô hình robot tự hành hoạt động trong môi trường có vật cản để tìm kiếm mục tiêu dựa trên cơ sở phân cấp các nhiệm vụ. Tiếp theo, bài báo phân tích ổn định của thuật toán điều khiển dựa trên lý thuyết ổn định Lyapunov.  Cuối cùng là kết quả mô phỏng kiểm chứng tính đúng đắn của thuật toán trên phần mềm Matlab.

Từ khóa: robot tự hành, hành vi dựa trên không gian rỗng.

Abstract:This paper has developed a model of autonomous robot operating in an environment with obstacles to find goal based on the decentralization of tasks. The next, the paper has stability analyzed of control algorithms base on Lyapunov theory. Finally, simulation results verify the correctness of the algorithm on Matlab software.

Keywords: Autonomous robot, Null Space based Behavior.

1. Giới thiệu chung

Robot tự hành là một kiểu robot có khả năng tự hoạt động, thực thi nhiệm vụ mà không cần sự can thiệp của con người. Robot tự hành ngày càng có nhiều ý nghĩa trong các ngành công nghiệp, thương mại, y tế, các ứng dụng khoa học và phục vụ đời sống của con người. Với sự phát triển của ngành Robot học, robot tự hành ngày càng có khả năng hoạt động trong các môi trường khác nhau, tùy mỗi lĩnh vực áp dụng mà chúng có nhiều loại khác nhau như robot sơn, robot hàn, robot cắt cỏ, robot thám hiểm đại dương, robot làm việc ngoài vũ trụ. Cùng với sự phát triển của yêu cầu trong thực tế, robot tự hành tiếp tục đưa ra những thách thức mới cho các nhà nghiên cứu. Vấn đề đặt ra của việc điều khiển robot tự hành là làm thế nào để robot có thể hoạt động, nhận biết môi trường và thực thi các nhiệm vụ đề ra mà không bị lỗi.

Trong nội dung bài báo này, chúng tôi đưa ra thuật toán điều khiển hành vi dựa trên không gian rỗng (Null Space based Behavior - NSB) để tính toán vận tốc di chuyển tới đích của robot tự hành trong môi trường có vật cản, tiếp theo bài báo phân tích sự ổn định của quá trình di chuyển trên cơ sở lý thuyết ổn định Lyapunov, cuối cùng là kết quả kiểm nghiệm thuật toán trên phần mềm Matlab.

2. Mô hình toán học của robot tự hành

2.1. Robot tự hành thực hiện một nhiệm vụ

Giả sử có một robot tự hành di chuyển trong không gian hai chiều với vận tốc u_rb.

Gọi                  

 

là vị trí của robot, lúc đó mô hình toán học của robot được mô tả như sau:

 

 

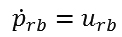 (1)

 

 

Gọi s - Biến được điều khiển để hoàn thành mục tiêu nhiệm vụ:

 (2)

 

 

Đạo hàm (2) theo thời gian ta được:

 (3)

 

 

 

Kết hợp (1) và (3): 

 

 

 

Trong đó: J(p) - Ma trận Jacobian J(p)    ` `    R^2x1

Trong đó: J⁺ - Ma trận giả nghịch đảo, J⁺   ` `   R^2x1

Ma trận rỗng N của J chính là hình chiếu của J lên phương vuông góc với J: N=I-J⁺J.

Gọi d là khoảng cách mong muốn đạt được, lúc đó (4) được viết lại như sau:

 (5)

 

 

Trong đó: l - Hệ số dương.

2.2. Robot tự hành thực hiện nhiều nhiệm vụ

Khi robot tự hành thực hiện nhiệm vụ di chuyển tới mục tiêu, trên đường di chuyển robot phải tránh được vật cản nằm trên đường đi để tránh bị hư hỏng. Lúc này robot sẽ phải thực hiện hai nhiệm vụ sau:

- Nhiệm vụ thứ nhất: Tránh vật cản;

- Nhiệm vụ thứ hai: Di chuyển tới mục tiêu.

Điều khiển robot dựa trên mức độ ưu tiên của các nhiệm vụ sau đó chiếu các nhiệm vụ có mức độ ưu tiên thấp hơn vào không gian rỗng của nhiệm vụ ưu tiên cao hơn được gọi là điều khiển hành vi dựa trên không gian rỗng [6]. Trong nội dung bài báo này, tác giả đã lựa chọn mức độ ưu tiên theo thứ tự: Tránh vật cản sau đó mới di chuyển đến mục tiêu. Với phương pháp tiếp cận điều khiển NSB, sơ đồ tổng hợp vận tốc của robot được trình bày trên Hình 2.1.

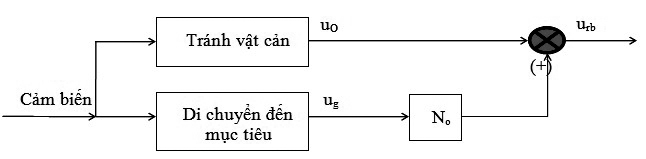Hình 2.1: Sơ đồ tổng hợp vận tốc di chuyển của robot

 

• Xác định vận tốc tránh vật cản:

Gọi

 

   

 

là vị trí của vật cản tĩnh, s_o Ỵ R là khoảng cách giữa robot và vật cản được xác định theo công thức:

 

 

 

Mong muốn của việc điều khiển robot tránh vật cản: khi vật cản nằm trong vùng di chuyển của robot tới mục tiêu thì robot phải cách vật cản ngoài không gian trên thì việc xuất hiện vật cản không làm ảnh hưởng đến tốc độ di chuyển của robot. Điều đó có nghĩa rằng tốc độ di chuyển của các cá thể robot  phụ thuộc vào khoảng cách giữa robot và vật cản.

Ma trận Jacobien  J₀  ` `  R^1x2   biểu diễn phương chiều của vận tốc di chuyển tránh vật cản:

 (6)        

 

 

 

Ma trận giả nghịch đảo của J_o:  J_g⁺ = p^_fpg  , J_g⁺  ` `    R^2x1

Ma trận rỗng của J_o:

 (7)

 

 

Từ (5) suy ra véc tơ vận tốc tránh vật cản của robot được xác định như sau:

 (8)

 

 

Trong đó:

 

                

 

Sai lệch giữa khoảng cách thực tế và khoảng cách mong muốn.

• Xác định vận tốc di chuyển đến mục tiêu:

Tương tự như tính vận tốc di chuyển tránh vật cản.

Gọi   

 

            

 

là vị trí của mục tiêu cần hướng tới, s_g Ỵ R là khoảng cách giữa robot thứ i và mục tiêu được xác định theo công thức:

 

 

 

 

Mong muốn của việc điều khiển robot di chuyển hướng tới đích là khoảng cách từ robot tới đích               .

Ma trận Jacobien J_g              : σ_g.d = d_g = 0

 

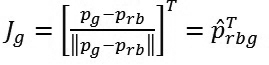(9)        

 

 

Ma trận giả nghịch đảo của J_g:  

Ma trận rỗng của J_g: J_g⁺ = p^_fpg  , J_g⁺  ` `    R^2x1

 (10)

 

 

Từ (5) suy ra véc tơ vận tốc tránh vật cản của robot được xác định như sau:

 (11)

 

 

Trong đó:                         

- Sai lệch giữa khoảng cách thực tế và khoảng cách mong muốn.

 

Tổng hợp vận tốc khi robot tự hành thực hiện cả hai nhiệm vụ:

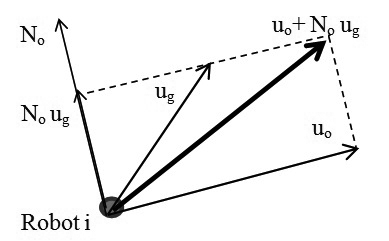Hình 2.2: Giản đồ tổng hợp vận tốc theo phương pháp NSB khi robot tự hành thực hiện hai nhiệm vụ

 

Vận tốc di chuyển của cá thể robot được tổng hợp theo phương pháp NSB:

 

(12)

 

Mục đích của việc điều khiển robot tự hành thực hiện hai nhiệm vụ: Tránh vật cản và tìm kiếm mục tiêu là sai lệch của mục tiêu nhiệm vụ

 

 

 

 

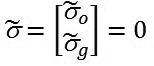Chọn hàm mục tiêu Lyapunop:

 

 

 

Đạo hàm V(.) theo thời gian: 

 

 

 

 

 

 

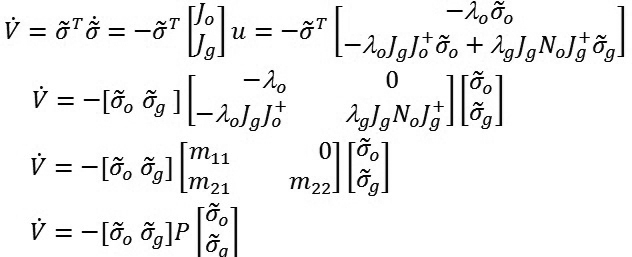Trong đó:   

 

 

 

Muốn  V >0 thì P>0. Theo định lý Sylvester, P >0 khi tất cả các phần tử nằm trên đường chéo chính là xác định dương:   m₁₁ > 0, m₁₂ > 0. Do đó, để P > 0 cần thỏa mãn đồng thời các điều kiện sau:

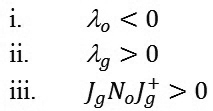 (13)

(14)

(15)

 

 

Điều kiện (15) đúng khi hai nhiệm vụ tránh vật cản o và tìm kiếm mục tiêu g là độc lập, có nghĩa là:                                                                         

 (16)

 

 

Trong đó: rank(.) - Hạng của ma trận.

Quá trình điều khiển robot tự hành có mô hình (12) thực hiện các nhiệm vụ di chuyển tới đích và tránh vật cản ổn định khi các điều kiện (13), (14) và (16) được thỏa mãn.

3. Kết quả mô phỏng

Tọa độ của robot, vật cản và đích được mô phỏng trên không gian 2 chiều [500;500]. Hình 2.3 mô phỏng quá trình di chuyển của robot tới đích, từ kết quả mô phỏng cho thấy:

i) Robot chỉ có thể thực hiện được hai mục tiêu nhiệm vụ khi `lambda` ` ` _og>0 (Hình 3.1a,3.1b,3.1c);

ii) Robot không tránh được vật cản khi `lambda` ` ` _o>0 (Hình 3.1d,3.1f);

iii) Robot không tìm thấy đích khi `lambda` ` ` _g(Hình 3.1e, 3.1f).

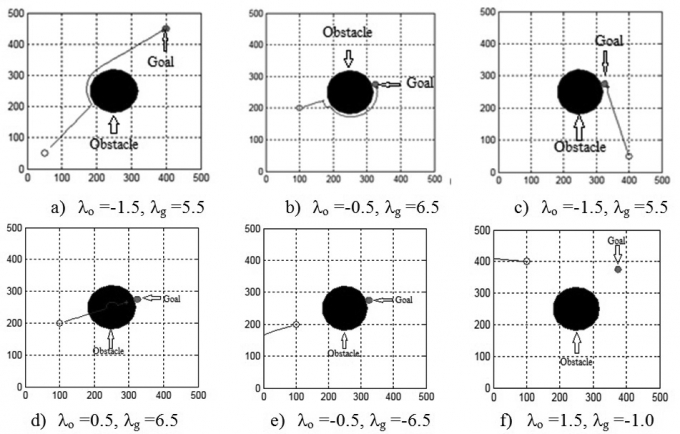Hình 3.1: Quá trình di chuyển tìm kiếm mục tiêu và tránh vật cản của robot tự hành

 

4. Kết luận

Bài báo đưa ra giải pháp điều khiển robot tự hành dựa trên cơ sở điều khiển hành vi không gian rỗng NSB, xây dựng luật điều khiển và chứng minh tính hôi tụ của thuật toán dựa trên cơ sở lý thuyết Lyapunov. Kết quả mô phỏng kiểm chứng thuật toán cho thấy: Robot tự hành tránh được vật cản và tìm thấy mục tiêu sau một thời gian di chuyển.

Tài liệu tham khảo

[1]. Jorge Lobo, Lino Marques, Jorge Dias, Urbano Nunes, Anfbal T. de Aimeida, Sensors for Mobile Robot Navigation, pp50-81.

[2]. , , Abe. K (1997), A mobile robot localization using ultrasonic sensors in indoor environment.

[3]. G. Golub, C. V. Loan (1996), Matrix Computations, 3rd ed. ed. Baltimore, MD: Johns Hopkins Univ. Press.

[4]. Johann Borenstein, Yoram Koren (April 1988), Obstacle Avoidance with Ultrasonic Sensors, IEEE Journal of Robotics and Automation, Vol. 4, No. 2, pp213-218.

[5]. C. G.Rusu, I. T.Birou (2010), Obstacle Avoidance Fuzzy System for Mobile Robot with IR Sensors, 10th International Conference on Development and Application Systems, Suceava, Romania, May 27-29, pp25-29.

[6]. G. (2008), Stability analysis for prioritized closed-loop inverse kinematic algorithms for redundant robotic systems, Robotics and Automation, IEEE International Conference on, pp 1993 - 1998.