Lựa chọn mô hình thiết kế bộ giảm chấn động lực TMD để giảm dao động cho cầu treo dân sinh tại VN

 

ThS. NCS. Nguyễn Trọng Nghĩa Trường Đại học Giao thông vận tải KS. Dương Văn Lạc GS. TSKH. Nguyễn Văn Khang Trường Đại học Bách khoa Hà Nội Người phản biện: PGS. TS. Nguyễn Phong Điền TS. Phạm Hoàng Kiên

Tóm tắt: Cầu treo dây võng là một giải pháp xây dựng cầu hiệu quả nhất trong điều kiện địa hình khó khăn phức tạp với yêu cầu vượt khẩu độ lớn. Cầu treo dây võng dân sinh cho tải trọng bộ hành và xe thô sơ rất phù hợp cho vùng núi xa xôi, hẻo lánh với nguồn kinh phí xây dựng thấp tại Việt Nam. Do kết cấu cầu treo dây võng là hệ có độ cứng nhỏ, biến dạng hình học lớn nên rất nhạy cảm với dao động theo phương thẳng đứng và dao động ngang. Khi những điều kiện cộng hưởng xảy ra thì thậm chí một chuyển dịch được coi là nhỏ của kết cấu dầm và/hoặc các tháp cầu cũng có thể gây ra sự mất ổn định động và gây ra tình trạng dao động rất mạnh cho các bộ phận kết cấu và dẫn đến phá hủy một phần hoặc toàn bộ kết cấu cầu. Vì vậy, việc nghiên cứu các giải pháp giảm dao động cho cầu treo dây võng nói chung và cầu treo dân sinh nói riêng là hết sức cần thiết và cần đưa vào từ giải pháp thiết kế. Bài báo tập trung phân tích lựa chọn mô hình thiết kế bộ giảm chấn động lực dạng khối lượng - lò xo (Tuned Mass Damper - TMD) để giảm giao động cho cầu treo dân sinh tại Việt Nam.

Từ khóa: Cầu treo dây võng, dao động riêng, bộ giảm chấn động lực.

Abstract: Suspension bridge is the most effective construction solutions in difficult terrain conditions, complex requirements and long span requirement. Suspension bridge for pedestrians load and non-motorized vehicles are suitable for mountainous areas, low-budget construction in Vietnam. Structure of suspension bridge is the small hardness, large displacement are sensitive to vertical and horizontal vibration. When the resonance condition occurs, even a small load is regarded as superstructure and / or the pylon can cause instability and causes very strong oscillation of the structural parts and lead to destruction of part or the entire bridge structure. Therefore, the study of solutions to reduce the vibration of suspension bridge is essential and should be included in the solution design. This article focuses on analyzing the solution for suspension bridge design using tuned mass damper (type masses - springs - TMD) to reduce vibration in Vietnam.

Keywords: Suspension bridge, eigen vibration, tuned mass damper (TMD).

1. Tổng quan

Cầu treo dây võng là dạng kết cấu cầu sử dụng để vượt khẩu độ nhịp lớn đã nhanh chóng trở nên phổ biến trên toàn thế giới do hiệu quả sử dụng cao về vật liệu, vẻ đẹp kiến trúc của công trình đặc biệt rất phù hợp tại các vị trí có địa hình phức tạp và hiểm trở. Tại Việt Nam, cầu treo dây võng được áp dụng phổ biến cho cầu treo nông thôn và cầu treo cho xe có tải trọng nhỏ, trong đó có Đề án xây dựng 186 cầu treo dân sinh đảm bảo ATGT trên phạm vi 28 tỉnh miền núi phía Bắc, miền Trung và Tây Nguyên đã được Bộ GTVT phê duyệt đề án tại Quyết định số 1906/QĐ-BGTVT. Lịch sử ngành Xây dựng cầu đã chứng kiến nhiều công trình cầu treo dây võng bị hư hỏng, thậm chí phá hủy hoàn toàn trong những điều kiện thông thường do dao động gây ra, điển hình là cầu treo dây võng Tacoma (1940), cầu Kutai Kartanegara ở Indonesia (2011), cầu Chinchu ở Trung Quốc (2007), cầu K'rông Bông ở Đăk Lăk (2013), cầu treo Chu Va 6 ở Lai Châu (2014)... Đối với cầu treo dây võng, kích thích tham số rất dễ xảy ra do sự có mặt của nhiều tần số thấp trong kết cấu dầm, tháp cầu và trong các dây cáp. Khi cộng hưởng xảy ra thì thậm chí một chuyển dịch được coi là nhỏ của kết cấu dầm và/hoặc các tháp cầu cũng có thể gây ra sự mất ổn định động và gây ra tình trạng dao động rất mạnh cho toàn bộ kết cấu. Biện pháp hiệu quả nhất để giảm dao động không mong muốn là ngăn chặn hoặc thay đổi nguồn gây ra dao động như: Tăng độ cứng của kết cấu, thay đổi khối lượng của kết cấu hoặc thay đổi hình dáng kết cấu phù hợp hơn về khí động học. Tuy nhiên, biện pháp này thường khó thực hiện được.

Lĩnh vực điều khiển dao động đã có những phát triển rất rộng trong những năm qua, đặc biệt sau sự cố sập cầu Tacoma, dạng điều khiển giảm dao động cơ bản là điều khiển chủ động, bị động và bán chủ động. Bố trí thiết bị giảm chấn là một giải pháp kinh tế cho bài toán ổn định dao động của công trình cầu dưới các tác dụng động lực học. Có rất nhiều hệ thống giảm chấn khác nhau đã ra đời nhưng đều tuân theo nguyên lý dao động cơ bản. Ứng dụng phổ biến nhất để giảm dao động cho cầu treo dây võng vẫn là bố trí thiết bị giảm chấn cho kết cấu nhịp. Thiết bị giảm chấn được sử dụng để giảm các tác động do gió bão, hoạt tải và tải trọng động đất. Với các công trình nằm tại vị trí ít chịu ảnh hưởng của động đất và gió bão thì chỉ cần nghiên cứu xem xét đến các tác động của hoạt tải. Các phân tích dưới đây tập trung phân tích ảnh hưởng của tải trọng người đi bộ lên kết cấu cầu treo dây võng và phân tích lựa chọn thiết kế bộ giảm chấn động lực dạng khối lượng - lò xo (viết tắt là bộ giảm chấn TMD) để giảm dao động cho cầu treo dân sinh tại Việt Nam.

2. Lựa chọn mô hình phân tích dao động với tải trọng người đi bộ

2.1. Mô hình tải trọng thẳng đứng và giá trị của tải trọng người đi bộ

Mô hình tải trọng người đi bộ được mô tả bằng 1 lực theo phương thẳng đứng Fp(t) (Hình 2.1) (theo các báo cáo [7], [8], [9]):

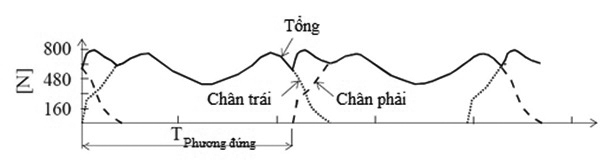Hình 2.1: Mô hình tải trọng thẳng đứng và giá trị của tải trọng người đi bộ

Triển khai phân tích lực này theo chuỗi Fourier:

 

(1)

 

Trong đó:

F(t) - Lực gây ra theo thời gian;

P - Trọng lượng tĩnh của người;

α_k - Hệ số của cấp điều hòa thứ k trong chuỗi Fourier  (Bảng 2.1);

f_p - Tần số bước đi của người (Bảng 2.2);

φ_k - Pha điều hòa thứ k.

Theo kết quả nghiên cứu [7], vận tốc di chuyển của người được xấp xỉ bằng 0,9 lần tần số di chuyển:

 

(2)

 

2.2. Thiết lập phương trình dao động cho mô hình dầm trên gối đàn hồi có gắn thêm các bộ giảm chấn

Xét mô hình dầm liên tục có gắn N_a bộ giảm chấn động lực (Hình 2.2)

Hình 2.2: Mô hình dầm có các bộ giảm chấn TMD

Phương trình dao động của hệ có dạng như sau:

 

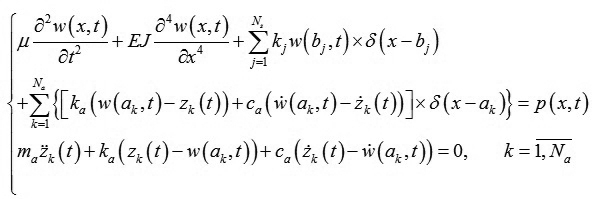 (3)

 

 

 

Điều kiện biên của hệ:        

 

(4)

 

Áp dụng phương pháp Ritz-Galerkin suy rộng và chú ý đến điều kiện biên (4), nghiệm của hệ phương trình đạo hàm riêng (3) được tìm dưới dạng:

 

(5)

 

Khi đó                

 

là nghiệm của hệ phương trình có dạng như sau:

    

 

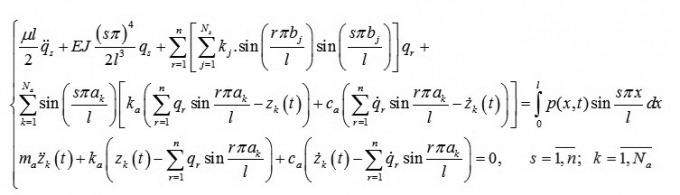(6)

 

 

Trong đó:

N_s - Số gối đàn hồi;

N_a  - Số bộ giảm chấn lắp trên cầu;

a_k - Khoảng cách từ bộ giảm chấn thứ k đến đầu cầu;

b_j - Khoảng cách từ gối thứ j đến đầu cầu;

k_j - Độ cứng của gối đàn hồi thứ j;

z_k - Tọa độ tuyệt đối của bộ giảm chấn thứ k.

Trong trường hợp nhiều người đi bộ trên cầu thì lực phân bố tác dụng lên dầm có dạng như sau:

 

(7)

 

Trong đó: F_p(t) được tính ở công thức (1);

v_p - Vận tốc của người di chuyển trên cầu (2);

d  - Khoảng cách giữa 2 người liên tiếp;

t_i  - Thời điểm người thứ i bắt đầu di chuyển trên cầu, t ₁ =(i-1) d/v;              ;

N_p - Số người di chuyển trên cầu;

H (t) - Hàm bước nhẩy.

Phương trình (6) được biến đổi như sau:

 

(8)

 

Có thể biến đối về dạng hệ phương trình vi phân cấp 2 như sau:

 

(9)

Tần số dao động riêng của dầm là nghiệm của phương trình sau:

 

(10)

2.3. Phân tích tính toán lựa chọn các thông số của bộ giảm chấn động lực TMD

Các bước tính toán xác định thông số bộ giảm chấn TMD trên cầu treo dây võng được thực hiện theo các bước đề xuất sau:

Bước 1: Xác định dạng dao động thứ r cần lắp đặt bộ giảm chấn để giảm dao động, từ đó suy ra vị trí cần lắp giảm chấn. Với mô hình cầu treo dây võng, 6 dạng dao động đầu tiên được xem xét bao gồm:

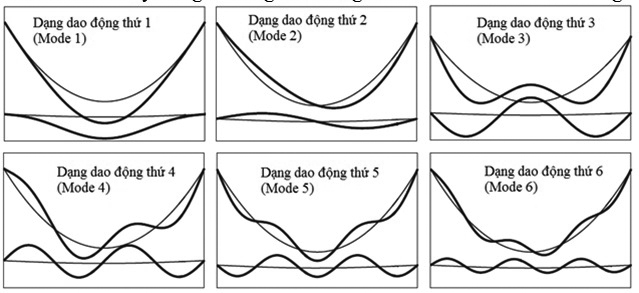Hình 2.3: Các dạng dao động của cầu treo dây võng

Trong đó, 3 dạng dao động đầu là các dao động có tần số thấp cần được xem xét trong bài toán xem xét lắp đặt hệ thống giảm chấn. Với dạng dao động 1 cần xem xét lắp đặt 1 bộ giảm chấn ở vị trí L/2; dạng dao động 2 cần xem xét lắp đặt 2 bộ giảm chấn ở vị trí L/4 và 3L/4; dạng dao động 3 cần xem xét lắp đặt 3 bộ giảm chấn ở vị trí L/4, L/2 và 3L/4. Như vậy, để giảm dao động của hệ cần xem xét lắp đặt 3 bộ giảm chấn ở các vị trí L/4, L/2 và 3L/4. Để đơn giản trong mô hình phân tích hệ nhiều bậc tự do về hệ một vật có khối lượng tương đương m^* và có tần số dao động ω_0r (Hình 2.4):

Hình 2.4: Mô hình hệ tương đương

Bước 2:  Xác định khối lượng và độ cứng quy đổi của dầm đựa theo [12, 5] được tính toán như sau:

 

 

Trong đó, m - Khối lượng của dầm, ω_0r - Tần số dao động riêng của dầm được xác định từ phương trình (10).

Bước 3: Lựa chọn hệ số:  

 

 

Bước 4: Xác định được khối lượng của bộ giảm chấn: 

 

 

Bước 5: Tính tần số dao động riêng của bộ giảm chấn:

 

 

 

Bước 6: Xác định độ cứng lò xo của bộ giảm chấn:

 

 

 

Bước 7: Xác định độ cản nhớt trong bộ giảm chấn:

 

 

 

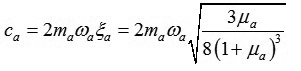Bước 8: Xác định khối lượng của mỗi bộ giảm chấn, vì dầm được quy về hệ một vật tương đương và một bộ giảm chấn, do vậy khi lắp r bộ giảm chấn để giảm dao động dạng thứ r thì thông số của mỗi bộ giảm chấn sẽ chia cho r.

 

 

 

3. Tính toán lựa chọn các thông số của bộ giảm chấn động lực cho cầu treo dây võng cho người đi bộ

Xét mô hình cầu treo dây võng có chiều dài nhịp L = 80m, chiều rộng cầu 1,5m, có 39 dây cáp treo với khoảng cách thiết kế là 2,0m, với các thông số:

 

 

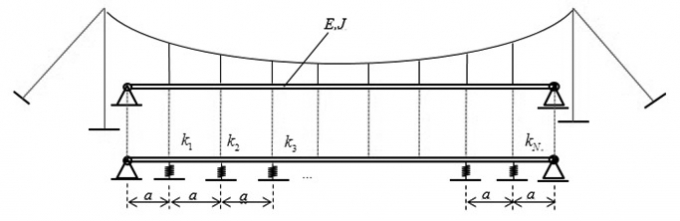Hình 3.1: Mô hình tính toán của cầu treo dây võng

 

Dao động của dầm được xác định:

 

 

 

Trong đó, q_s - Nghiệm của phương trình (9).

Tần số dao động riêng của cầu là nghiệm của phương trình (10).

Mô hình phân tích cho hệ 39 cáp treo được quy đổi thành 39 gối lò xo có độ cứng như sau:

Bảng 3.1. Độ cứng của các lò xo (kN/m)

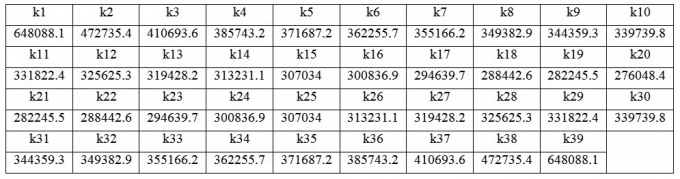Sử dụng chương trình Matlab^® 2010 để lập trình tính toán tần số dao động riêng của cầu (Bảng 3.2):

Bảng 3.2. Tần số dao đông riêng của cầu với mô hình 39 gối đàn hồi tương đương 39 cáp treo

Khối lượng của mỗi người đi bộ được lấy là 70kg, khoảng tần số di chuyển 1,4 - 2,4 Hz và bỏ qua tần số cao trong khai triển (1), ta có:

 

(11)

 

3.1. Tính toán cho bộ giảm chấn được lắp ở vị trí L/2 để giảm dạng dao động thứ nhất

- Xác định khối lượng và độ cứng quy đổi của dầm như sau:

 

 

- Lựa chọn hệ số:

 

 

- Xác định được khối lượng của bộ giảm chấn: 

 

        

- Tính tần số dao động riêng của bộ giảm chấn: 

 

       

 

- Xác định độ cứng lò xo của bộ giảm chấn:             

 

 

 

- Xác định độ cản nhớt trong bộ giảm chấn:  

 

 

 

3.2. Tính toán cho bộ giảm chấn được lắp ở vị trí L/4 và 3L/4 để giảm dạng dao động thứ hai (tương tự như mục 3.1)

Thực hiện tính toán tương tự mục 3.1, có thể xác định thông số kỹ thuật của bộ giảm chấn như sau: Độ cứng lò xo của bộ giảm chấn: k _a = 2,97.10⁴ [N/m] độ cản nhớt trong bộ giảm chấn C _a = 130,1[Nm/s].

3.3. Kết quả tính toán

Xét hai dạng dao động nguy hiểm là dạng dao động thứ nhất và thứ hai, để khảo sát hiệu quả giảm chấn của bộ giảm chấn chúng ta cho tần số dao động di chuyển của người gần những tần số dao động riêng này (Bảng 3.3), việc tính toán với giả thiết là có 50 người lần đi liên tiếp qua cầu khoảng cách giữa hai người liên tiếp là 2m.

Bảng 3.3. Tần số dao đông riêng của 3 dạng dao động riêng đầu tiên trước khi và sau khi lắp đặt bộ giảm chấn TMD

 

Tính với tần số của đoàn người di chuyển bằng tần số dạng dao động riêng thứ nhất ƒ_p = ƒ₀₁ =4,1961 Hz

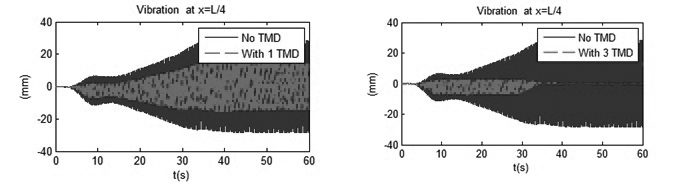Hình 3.2: So sánh kết quả tại mặt cắt L/4

 

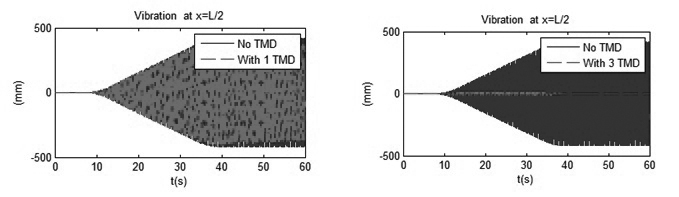Hình 3.3: So sánh kết quả tại mặt cắt L/2

 

Tính với tần số của đoàn người di chuyển bằng tần số dạng dao động riêng thứ hai ƒ_p = ƒ₀₂ = 4,383 Hz

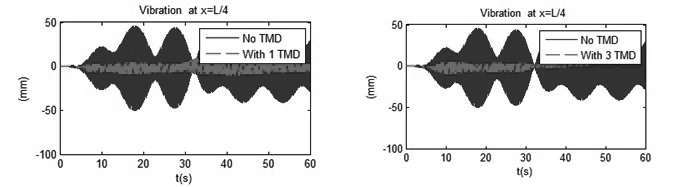Hình 3.4: So sánh kết quả tại mặt cắt L/4

 

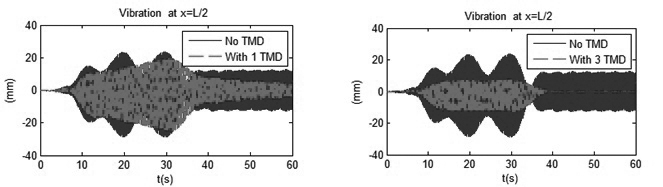Hình 3.5: So sánh kết quả tại mặt cắt L/2

 

Tính với tần số của đoàn người di chuyển bằng tần số dạng dao động riêng thứ ba ƒ_p=ƒ₀₃ = 4,4885Hz

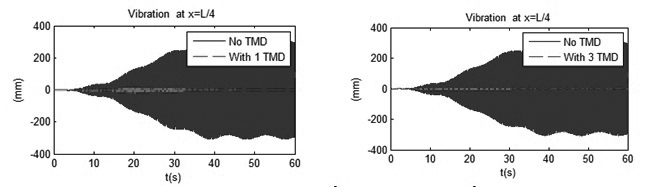Hình 3.6: So sánh kết quả tại mặt cắt L/4

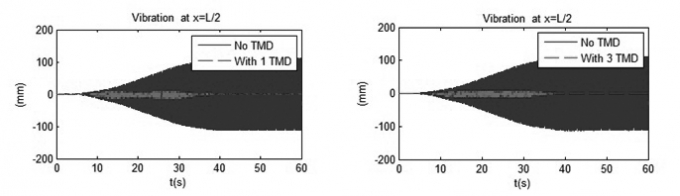Hình 3.7: So sánh kết quả tại mặt cắt L/2

4. Kết luận

Với bộ giảm chấn TMD có khối lượng xấp xỉ 1% khối lượng của kết cấu nhịp có thể tránh được hiện tượng cộng hưởng, có thể giảm biên độ dao động đáng kể từ 0,5m (biên độ gần với biên độ xảy ra cộng hưởng) xuống còn gần 11mm sẽ tăng được năng lực khai thác, tuổi thọ khai thác cầu tránh hiện tượng hư hỏng do mỏi, tạo tâm lý thoải mái cho người đi bộ khi qua cầu.

Kết quả tính toán cho thấy, sử dụng 3 bộ giảm chấn giảm biên độ dao động tốt hơn một bộ giảm chấn. Hai vị trí lắp đặt bộ giảm chấn ở vị trí L/4 và 3L/4 cho hiệu quả tắt dao động của dạng dao động thứ nhất được thể hiện rõ ở Hình 3.2 và 3.3. Với kết quả phân tích trên có thể sử dụng để lựa chọn thiết kế bộ giảm chấn động lực dạng khối lượng - lò xo cho cầu treo dây võng cho người đi bộ. Do các công trình cầu khác nhau có khối lượng và kích thước không hoàn toàn như nhau, nên việc chọn các tham số của bộ giảm chấn phải phù hợp với từng cầu. Nhóm tác giả hy vọng Bộ GTVT, Tổng cục ĐBVN xem xét cho khảo sát, thiết kế và ứng dụng trên một số công trình cầu cụ thể để đo đạc đánh giá với kết quả nghiên cứu lý thuyết làm căn cứ chỉnh sửa mô hình lý thuyết và triển khai rộng rãi cho nhiều công trình cầu treo dây võng cho người đi bộ tại Việt Nam o

Tài liệu tham khảo

[1]. Nguyễn Văn Khang (2005), Dao động kỹ thuật, NXB. Khoa học Kỹ thuật, Hà Nội.

[2]. Den Hartog J.P. (1956), Mechanical Vibrations, McGraw-Hill, New York.

[3]. D. Younesian1, A. Nankali, E. Motieyan (2011), Optimal Nonlinear Energy Sinks in Vibration Mitigation of the Beams Traversed by Successive Moving Loads, Journal of Solid Mechanics, Vol. 3, No. 4,  pp. 323-331.

[4]. Yung-Hsiang Chen (2007), Vibrational Control of a Beam to Moving Loads or Earthquake by Tuned Mass Dampers, ISEV.

[5]. Yung-Hsiang Chen, Ding-ShinChen (2004), Timoshenko Beam with Tuned Mass Dampers to Moving Loads, J. Bridge Eng, 2004.9:167-177.

[6]. Renata M. Soares, Zenon J.G.N. del Prado, Paulo B. Gonçalves (2010), On the vibration control of beams using a moving absorber and subjected to moving loads, Mecánica Computacional, Vol XXIX, pages. 1829-1840.

[7]. G.B. Warburton (1981), Optimum  absorber  parameters  for  minimizing  vibration  response,  Earthquake  Eng.  Struct.  Dyn.  9, 251-262.

[8]. Nicolacarprineto, Walterlacabonara, Fabriziovestroni (2010), Mitigation of Pedestrian-induced Vibrations in Suspension Footbridges via Multiple Tuned Mass Dampers, Journal of Vibration and Control, 16(5), 749-776.

[9]. Zivanovic, S., Pavic, A., and Reynolds, P. (2005), Vibration serviceability of footbridges under human-induced excitation: a literature review, Journal of Sound and Vibration 279, 1-74.

[10]. J.M.W.Brownjohn (1997), Vibration characteristic of a suspension footbridge, Journal of Soundand Vibration 202(1), 29-46.

[11]. D Younesian , M H Kargarnovin, and E Esmailzadeh (2008), Optimal passive vibration control of  Timoshenko beams with arbitrary boundary conditions traversed by moving loads, Journal of Multi-body Dynamics, 222: 179.

[12]. Jae-SeungHwanga, HongjinKimb, JinkooKimc (2006),  Estimation of the modal mass of a structure with atuned-mass damper using H-infinity optimal model reduction, Engineering Structures 28, 34-42.