Nghiên cứu khả năng giảm sóng tràn của khối phủ Rakuna IV cho đê đá đổ mái nghiêng bằng mô hình toán IH2-VOF

TS. Lê Thị Hương Giang Trường Đại học Hàng hải Việt Nam Người phản biện: TS. Trần Ngọc An TS. Bùi Quốc Bình

TÓM TẮT: Bài báo trình bày kết quả nghiên cứu khả năng chiết giảm sóng tràn của khối phủ Rakuna IV cho đê đá đổ mái nghiêng bằng mô hình toán IH2-VOF. Đây là một trong số các khối phủ được phát minh bởi Công ty Nikken Kogaku (Nhật Bản) năm 2007. Các kịch bản kiểm định mô hình được thực hiện cho mặt cắt số 4 đê chắn sóng Nghi Sơn - Thanh Hóa. Phạm vi của nghiên cứu này là cho đê đá đổ mái nghiêng phủ hai lớp Rakuna IV trong điều kiện có sóng tràn và sóng không vỡ.

Qua kết quả mô phỏng tương tác sóng - đê bằng mô hình máng sóng số IH2 - VOF đã giải thích được tính chất phụ thuộc của độ nhám gr vào số Iribarren ξm-1, 0 thông qua hiệu ứng đệm nước.

TỪ KHÓA: Sóng tràn, đê đá đổ mái nghiêng, mô hình toán IH2-VOF.

Abstract: This  paper presents the research result on the overtopping reduction capacity of Rakuna IV armour unit for rubble mound breakwater by numerical flume IH2 - VOF. Rakuna IV is one of armour unit invented by Nikken Kogaku (Japan)in 2007. The model validation and adjustment of numerical flume IH2 - VOF is carried out based on physical flume for section 4 of Nghi son breakwater.

This research is limited to the type of rubble mound breakwater with two-layer Rakuna-IV and to non-breaking waves. These scenarios result of wave-breakwater interaction by IH2 - VOF model explained clearly the dependence of gr  on Iribarren number xm-1, 0 by “water buffer”.

KEYWORDS: Wave overtopping, tilted roof rockfill dike, IH2 - VOF mathematical model.

1. Đặt vấn đề

Mô hình IH2-VOF là máng sóng số họ RANS-VOF, đã có một bề dày lịch sử nhiều năm phát triển, khởi đầu từ nhóm nghiên cứu của Giáo sư Phillips Liu ở Trường Đại học Cornell - Mỹ (Liu và nnk, 1999). Trong những năm gần đây, mô hình này đã được Viện Thủy lực của Trường Đại học Cantabria (Tây Ban Nha) tiếp tục nghiên cứu phát triển, mở rộng tính năng và đã trở thành một máng sóng số được đánh giá là hiện đại với mức độ tin cậy bậc nhất thế giới hiện nay. IH2-VOF có khả năng mô phỏng tương tác sóng với công trình biển với các tính năng tương tự như trong mô hình vật lý máng sóng. Dạng công trình có thể mô phỏng trong mô hình có cấu tạo kết cấu tương tự như trong thực tế là dạng không thấm (đặc) hoặc cho phép dòng chảy qua (thấm) như lõi đê đá đổ, thân đê cát… và có thể cấu tạo hình học bất kỳ: Mái nghiêng, tường đứng hoặc hỗn hợp. Các kết quả mô phỏng tương tác là trường dòng chảy, trường áp lực, trường rối, áp lực sóng lên kết cấu bê tông, sóng leo, sóng tràn qua công trình.

2. HỆ PHƯƠNG TRÌNH CƠ BẢN

Mô hình dựa trên hệ phương trình trung bình Reynolds Navier - Stockes 2 chiều

 

 

 

 

 

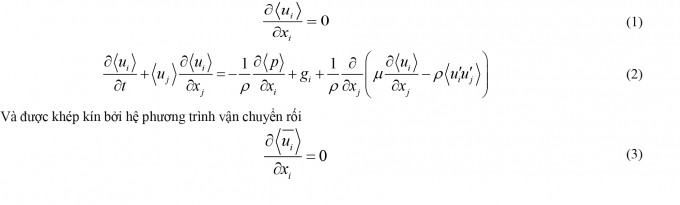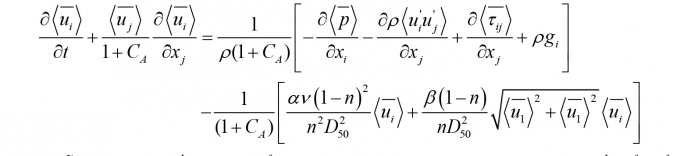 (4)

 

 

Mặt thoáng ngẫu nhiên của chất lỏng chuyển động được mô tả thông qua phương trình biến đổi thể tích VOF của khối chất lỏng xem xét:

 

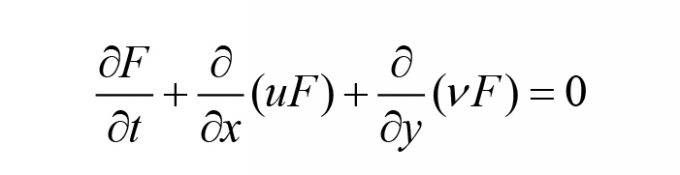(5)

 

 

Kết quả mô phỏng tương tác sóng - công trình của mô hình chịu ảnh hưởng nhiều bởi các hệ số cản tuyến tính α và hệ số cản phi tuyến β. Đây là hai hệ số phụ thuộc chủ yếu vào kích thước và độ rỗng của khối phủ.

 

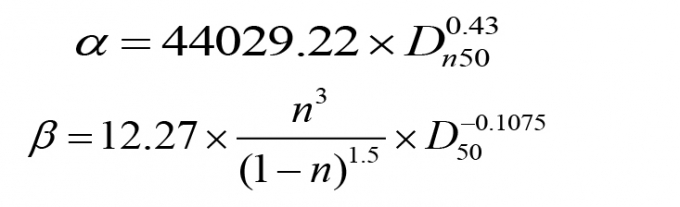(6)

 

 

Van Gent (1995) cũng đưa ra phương pháp xác định hệ số cản phi tuyến β đối với đê đá đổ:

 

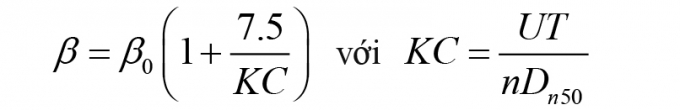(7)

 

3. KIỂM ĐỊNH VÀ HIỆU CHỈNH MÔ HÌNH

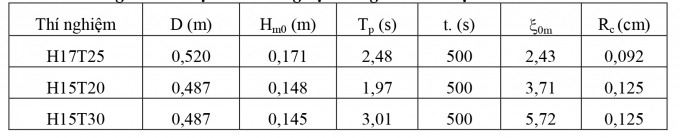
Việc hiệu chỉnh và kiểm định mô hình máng sóng số IH2 - VOF được thực hiện trên cơ sở mô hình thí nghiệm vật lý cho mặt cắt số 4 đê chắn sóng Nghi Sơn. Các thí nghiệm dùng cho kiểm định đã được thực hiện trong máng sóng Trường Đại học Thủy lợi với 3 kịch bản sóng tràn khác nhau. Các thí nghiệm mô hình vật lý lựa chọn cho kiểm định mô hình toán được trình bày ở Bảng 3.1.

Bảng 3.1. Các kịch bản thí nghiệm dùng cho kiểm định mô hình toán

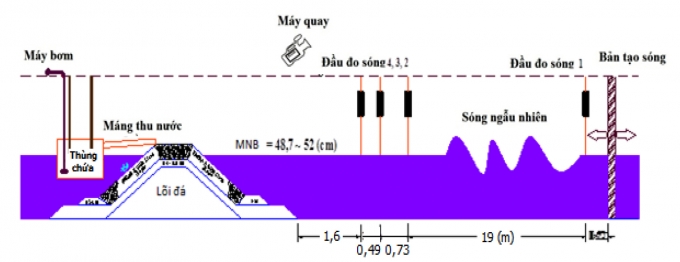Hình 3.1: Sơ đồ bố trí thí nghiệm trong mô hình vật lý

Không gian của mô hình toán được thiết lập tương tự như mô hình vật lý với hai đầu đo được thiết lập trong mô hình máng sóng số. Đầu đo số 1 được bố trí cách nguồn tạo sóng 19m, đầu đo số 2 được bố trí ngay tại mép đỉnh đê phía sau đo lưu lượng tràn qua đỉnh đê (Hình 3.1).

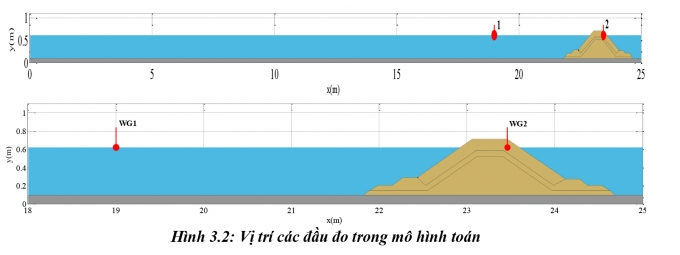
Máng sóng trong mô hình toán có kích thước (dài cao) là 28m x 1,1m và được rời rạc hóa thành 140 x 11 ô lưới chữ nhật không đều có kích cỡ nhỏ nhất là 0,02m theo phương ngang và 0,01m theo phương đứng (Hình 3.2).

 

Sử dụng số liệu sóng thực đo tại vị trí đầu đo số 1 ở mô hình vật lý theo dạng phổ JONSWAP chuẩn làm số liệu sóng đầu vào cho mô hình toán. Sóng thực đo tại vị trí đầu đo số 2 được sử dụng để so sánh với sóng trong mô hình toán.

Hình 3.3 và Hình 3.4 lần lượt minh họa kết quả so sánh đường quá trình sóng và phổ sóng cho trường hợp H17T25. Kết quả cho thấy có sự phù hợp khá tốt giữa kết quả tính toán và thực đo.

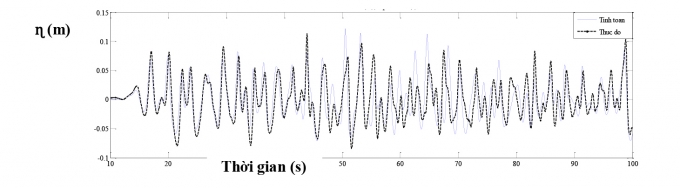Hình 3.3: Kết quả kiểm định đường quá trình sóng ở điều kiện mực nước 0,52m

 

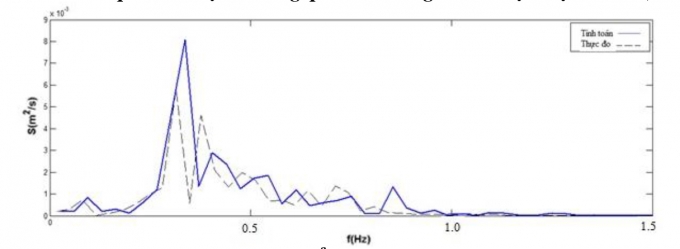Hình 3.4: So sánh phổ sóng tính toán và thực đo

Hệ số α và β không chỉ phụ thuộc vào kích thước vật liệu mà còn phụ thuộc vào tính chất của quá trình tương tác của sóng trên mái đê, do vậy tác giả đã hiệu chỉnh hai hệ số này nhằm tìm ra bộ giá trị phù hợp nhất. Kết quả kiểm định và các tham số hiệu chỉnh theo sự phù hợp về lưu lượng sóng tràn trung bình được thể hiện ở Bảng 3.2.

Bảng 3.2. Kết quả hiệu chỉnh và kiểm định các thông số độ nhạy mô hình

4. HIỆU ỨNG ĐỆM NƯỚC

Hiệu ứng đệm nước được cho là yếu tố dẫn tới sự phụ thuộc của hệ số chiết giảm sóng tràn γr vào ξm-1, 0 hay là vào tính chất tương tác của sóng trên mái đê. Để làm sáng tỏ sự hình thành đệm nước, tác giả đã tiến hành mô phỏng đánh giá tương tác sóng - đê bằng máng sóng số với các tham số đã được kiểm định cho ba kịch bản: Sóng dài (H = 0,145m, T = 3,01s, ξm-1, 0 lớn), sóng ngắn (H = 0,148m, T = 1,97s, ξm-1, 0 nhỏ) và đê dùng khối phủ có độ rỗng nhỏ hơn trong trường hợp sóng dài. Kết quả mô phỏng cho thấy, với sóng càng dài (ξ0m lớn) (so sánh Hình 4.1 và Hình 4.2) hoặc với cùng một điều kiện sóng nhưng độ rỗng lớn (so sánh Hình 4.1 và Hình 4.2) thì đệm nước hình thành càng rõ rệt, độ nhám của mái khối phủ, do đó càng giảm (γr lớn) thể hiện qua thời gian sóng rút Δt và phạm vi phân bố lưu tốc u ≈ 0 (đệm nước) xung quanh phía ngoài đê, điều này phù hợp với kết quả nghiên cứu trên mô hình vật lý.

 

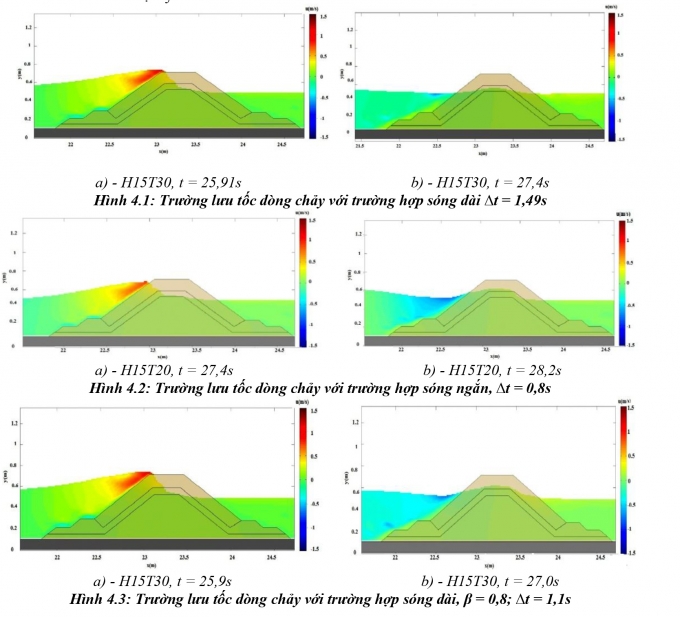5. KẾT LUẬN VÀ KIẾN NGHỊ

Kế thừa kết quả thí nghiệm mô hình máng sóng vật lý (đã xác định được hệ số chiết giảm sóng tràn gr cho khối phủ RAKUNA IV ứng với 2 khoảng số Iribarren xm-1, 0 khác nhau) và qua kết quả mô phỏng tương tác sóng - đê bằng mô hình máng sóng số IH2 - VOF đã giải thích được tính chất phụ thuộc của hệ số chiết giảm sóng tràn gr vào số Iribarren xm-1, 0 thông qua hiệu ứng đệm nước.

Tài liệu tham khảo

[1]. Bruce, T., Van der Meer, J.W., Franco, L., Pearson, J.M. (2009), Overtopping performance of different armour units for rubble mound breakwaters, Coastal Engineering, 56, pp. 166-179.

[2]. Burcharth, H.F., Christensen, M. Jensen, T. and Frigaard, P. (1998), Influence of core permeability on Accropode armour layer stability, Proceedings International conference coastlines, structures and breakwaters, Institution of Civil Engineers, Thomas Telford, London, pp. 34-45.

[3]. Tuan, T.Q., Masushita, H., Luong, N.Q., Hai, L.T, Hai, P.T and Taki, Y. (2011), Experimental study on stability of Nikken Kogaku’s new wave dissipating blocks in application to coastal protection works in Vietnam, Report of Joint Research WRU-NIKKEN KOGAKU, 137 pp.

[4]. Van der Meer, J.W. (1988), Stability of Cubes, Tetrapods and Accropode, Design of Breakwaters, Thomas Telford, Proc. Breakwaters ‘88 Conference, Eastbourne.

[5]. Van der Meer, J.W. (1999), Design of concrete armour layers, http://www.vandermeerconsulting.nl.

[6]. Zelt, J.A. and Skjelbreia, J.E. (1992), Estimating incident and reflected wave fields using an arbitrary number of wave gauges, Proc. 23rd Int. Conf. Coastal Eng., ASCE, pp. 777-789.