Nghiên cứu ổn định dao động uốn xoắn của hệ cánh - cánh liệng dưới tác dụng của các lực khí động bằng phương pháp phân tích trị riêng phức

TS. Lê Quốc Tiến Trường Đại học Hàng hải Việt Nam Người phản biện: TS. Trần Ngọc An TS. Lê Thị Hương Giang

Tóm tắt: Trong bài báo, tác giả trình bày việc tính toán ổn định dao động uốn xoắn của hệ cánh - cánh liệng dưới tác dụng của các lực khí động bằng phương pháp phân tích trị riêng phức. Sau đó, ổn định dao động uốn xoắn của một hệ cánh - cánh liệng cụ thể được tính toán mô phỏng số.

Từ khóa: Hệ cánh - cánh liệng, ổn định dao động uốn xoắn, các lực khí động, phương pháp phân tích trị riêng phức.

Abstract: In this paper, the author use the complex eigenvalue method to calculate the flutter stability of a wing-aileron system under wind action. Then, the stability of an oscillating wing-aileron system is numerically simiulated.

Keywords: Wing-aileron system, flutter stability, aerodynamic forces and moments, the complex eigenvalue method.

1. ĐẶT VẤN ĐỀ

Trong tài liệu [13], tác giả Theodore Theodorsen đã đưa ra việc sử dụng cánh liệng (aileron) để điều khiển bị động dao động uốn xoắn của cánh (wing) dưới tác dụng của các lực khí động. Dao động uốn xoắn của hệ cánh - cánh liệng cũng được trình bày trong các tài liệu chuyên ngành về khí động học [1, 8]. Các nghiên cứu hiện nay về dao động hệ cánh - cánh liệng đi theo hai hướng: Điều khiển bị động [4, 5, 7, 10, 11] và điều khiển chủ động [3, 9, 12].

Năm 2014, Trường Đại học Hàng hải Việt Nam được Bộ GTVT giao phụ trách Dự án Phòng thí nghiệm trọng điểm - Bể thử mô hình tàu thủy nhằm giải quyết các vấn đề khoa học và công nghệ thuộc các lĩnh vực: Kỹ thuật tàu thủy, kỹ thuật biển, thủy khí động lực học và một số lĩnh vực kỹ thuật công nghiệp khác.

Trong quá trình thực hiện dự án, ngoài việc giải quyết nguồn vốn của dự án thì việc làm chủ được công nghệ cũng như nắm vững cơ sở lý thuyết của các lĩnh vực đã nêu ở trên là hết sức cần thiết. Với mục đích đáp ứng một phần nhỏ các yêu cầu trên, trong nội dung bài báo này, tác giả trình bày nghiên cứu dao động uốn xoắn của hệ cánh - cánh liệng dưới tác dụng của các lực khí động theo phương pháp phân tích trị riêng phức. Đây là một trong những bài toán cơ bản thường được xây dựng mô hình thực nghiệm trong ống thổi khí động (nằm trong nội dung của Dự án). Tác giả tập trung giải quyết việc tìm thông số độ cản cũng như tần số dao động của hệ cánh - cánh liệng trên toàn miền vận tốc gió.

2. MÔ HÌNH NGHIÊN CỨU VÀ PHƯƠNG TRÌNH CHUYỂN ĐỘNG

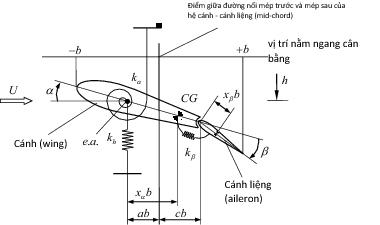Hình 2.1: Mô hình mặt cắt của hệ cánh - cánh liệng [1, 4, 5, 7, 8, 10, 11, 12, 13]

Xét mô hình mặt cắt của hệ cánh - cánh liệng như trên Hình 2.1. Hệ giả thiết có ba bậc tự do: Chuyển vị uốn và chuyển vị xoắn của cánh, ký hiệu bởi h và α, cùng với chuyển vị xoắn tương đối của cánh liệng, ký hiệu b. Các ký hiệu được sử dụng trên Hình 2.1, gồm có: 2b - Tổng chiều dài của cánh và cánh liệng; ab - Khoảng cách từ tâm uốn của cánh (tập hợp các điểm tâm uốn gọi là trục đàn hồi - elastic axis (e.a.) đến điểm mid-chord; x_αb - Khoảng cách từ khối tâm của hệ cánh - cánh liệng đến tâm uốn; cb - Khoảng cách từ trục quay của cánh liệng đến điểm mid-chord; x_bb - Khoảng cách từ khối tâm của cánh liệng đến trục quay của cánh liệng. Các đại lượng a, x_α, c, x_b có giá trị dương khi nằm phía cánh liệng so với điểm mid-chord.

Để thiết lập phương trình chuyển động của hệ trên, ta có thể sử dụng nguyên lý d’Alembert hoặc phương trình Lagrange loại II. Theo các tài liệu [1, 5, 10, 11, 12, 13], trong trường hợp cánh liệng điều khiển bị động, phương trình chuyển động của mô hình mặt cắt hệ cánh - cánh liệng có dạng:

 

 

 

Trong đó: m - Khối lượng trên một đơn vị dài của cánh và cánh liệng; S_α, I_α - Mô-men tĩnh và mô-men quán tính của hệ cánh - cánh liệng lấy đối với trục đàn hồi của cánh; S_β, I_β - Mô-men tĩnh và mô-men quán tính của cánh liệng lấy đối với trục quay của cánh liệng; k_h, k_α, k_β - Độ cứng chống uốn của cánh trên một đơn vị chiều dài, độ cứng chống xoắn của cánh đối với trục đàn hồi trên một đơn vị chiều dài và độ cứng chống xoắn của cánh liệng đối với trục quay của cánh liệng trên một đơn vị chiều dài; L, M_α, M_β - Lần lượt là lực nâng và mô-men khí động tác dụng lên cánh và mô-men khí động tác dụng lên cánh liệng.

3. PHƯƠNG TRÌNH LỰC KHÍ ĐỘNG

Trong trường hợp cánh và cánh liệng được xem như các tấm mỏng, phẳng, theo các tài liệu [1, 5, 10, 11, 13], các lực và mô-men khí động có dạng:

 

                                   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

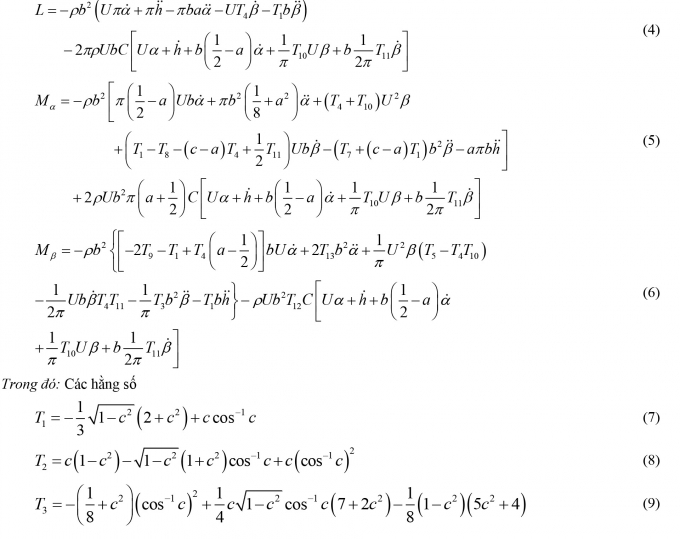5. VÍ DỤ ÁP DỤNG

Xét mô hình cánh - cánh liệng được tiến hành thực nghiệm theo tài liệu tham khảo [4] có các thông số như trên Bảng 5.1:

Bảng 5.1. Các thông số của mô hình cánh - cánh liệng (phụ lục A của tài liệu [4])

Các thông số hình học
Tổng chiều dài cánh + cánh liệng 2b	0,254 m
Chiều dài nhịp thực nghiệm s	0,52 m
Một nửa tổng chiều dài cánh + cánh liệng b	0,127 m
Vị trí tương đối của trục đàn hồi a	-0,5
Vị trí tương đối của trục quay cánh liệng c	0,5
Các thông số khối lượng
Khối lượng của cánh	0,62868 kg
Khối lượng của cánh liệng	0,18597 kg
Khối lượng trên 1 m dài của hệ cánh-cánh liệng m	1,558 kg/m
Các thông số quán tính
Mô-men tĩnh Sα (trên 1m dài)	0,08587 kgm
Mô-men tĩnh Sβ (trên 1m dài)	0,00395 kgm
xα	0,434
xβ	0,01996
Mô-men quán tính Iα (trên 1m dài)	0,01347 kgm2
Mô-men quán tính Iβ (trên 1m dài)	0,0003264 kgm2
Các thông số độ cứng
Độ cứng thu gọn kα* (trên 1m dài)	1.486 1/s2
Độ cứng thu gọn kβ* (trên 1m dài)	155 1/s2
Độ cứng thu gọn kh* (trên 1m dài)	1.809 1/s2
Các thông số độ cản
Độ cản Loga δα	0,01626
Độ cản Loga δβ	0,0115
Độ cản Loga δh	0,0113

Cần chú ý rằng, theo tài liệu [4], các độ cứng thu gọn được tính theo các công thức sau:

 

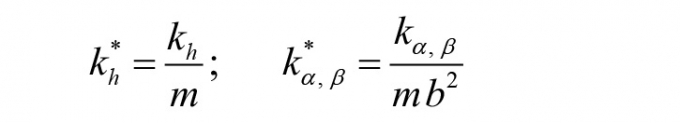 (27)

Sử dụng phương pháp phân tích trị riêng phức đã nêu ở trên và giải các phương trình bằng phần mềm Matlab, các kết quả thu được như trên Hình 5.1:

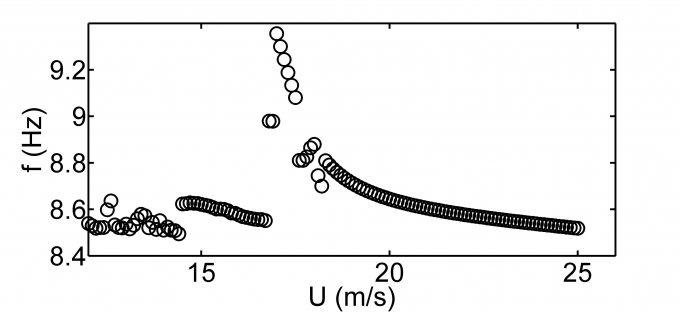
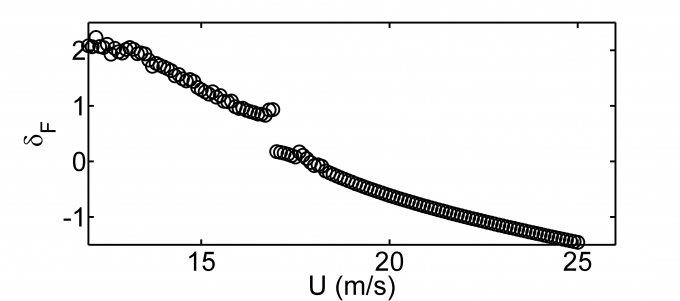
Hình 5.1: Đồ thị quan hệ U - f  và U - d_F

Vận tốc tới hạn được xác định theo phương pháp phân tích trị riêng phức là 17,9m/s. Kết quả thực nghiệm trong tài liệu [4] là 20,6m/s. Sai số giữa kết quả tính toán và kết quả thực nghiệm là -13,11%.

6. KẾT LUẬN

Trong nội dung bài báo, tác giả trình bày việc sử dụng phương pháp phân tích trị riêng phức để tính toán ổn định dao động uốn xoắn của hệ cánh - cánh liệng. Tác giả tập trung vào việc xác định độ cản và tần số dao động của hệ trên toàn miền vận tốc gió (dưới tới hạn, tại vị trí tới hạn và trên tới hạn). Kết quả tính toán vận tốc tới hạn trong ví dụ phù hợp tốt với kết quả thực nghiệm trong tài liệu tham khảo, điều đó cho thấy độ tin cậy của quá trình tính toán. Nghiên cứu dao động của hệ cánh - cánh liệng là một trong những bài toán cơ bản trong tiến hành thực nghiệm của ống thổi khí động.

Tài liệu tham khảo

[1]. R.L. Bisplinghoff, H. Ashley, R.L. Halfman (1995), Aeroelasticity, Dover Publications, Inc.

[2]. R.L. Bisplinghoff, H. Ashley (1962), Principles of aeroelasticity, Dover Publications, Inc.

[3]. D. Borglund, J. Kuttenkeuler (2002), Active wing flutter suppression using a trailing edge flap, Journal of Fluids and Structures 16(3), pp. 271-294

[4]. M.D. Conner, D.M. Tang, E.H. Dowell, L.N. Virgin (1997), Nonlinear behavior of a typical airfoil section with control surface freeplay: A numerical and experimental study, Journal of Fluids and Structures 11, pp. 89-109.

[5]. D. Dessi, F. Mastroddi (2004), Limit-cycle stability reversal via singular perturbation and wing-flap flutter, Journal of Fluids and Structures 19, pp. 765-783.

[6]. E.H. Dowell (Editor) (2005), A modern course in aeroelasticity, Kluwer Academic Publisher.

[7]. E.H. Dowell, J.P. Thomas, K.C. Hall (2004), Transonic limit cycle oscillation analysis using reduced order aerodynamic models, Journal of Fluids and Structures 19, pp. 17-27.

[8]. Y.C. Fung (1993), An Introduction to the Theory of Aeroelasticity, Dover Publications, Inc (NewYork).

[9]. Nhan Nguyen, Eric Ting (2014), Flutter analysis of mission-adaptive wing with variable camber continuos trailing edge flap, American Institute of Aeronautics and Astronautics, AIAA SciTech 13-17 January, National Harbor, Maryland.

[10]. Hatem Rahim Wasmi, Ali Abdul Mohsin Hasan, Waleed Jasim Mhaimeed (2015), Aeroelastic Flutter of Subsonic Aircraft Wing Section with Control Surface, Journal of Engineering, Number 12, Volume 21, pp. 104-123.

[11]. Udbhav Sharma (2005), Effects of cubic hardening nonlinearities on the flutter of a three degree of freedom airfoil, School of Aerospace Engineering, Georgia Institute of Technology.

[12]. Samuel da Silva, Vicente L. Júnior (2006), Active flutter suppression in a 2-D airfoil using linear matrix inequalities techniques, Journal of the Brazilian Society of Mechanical Sciences and Engineering, pp. 84-93.

[13]. Theodore Theodorsen (1935), General theory of aerodynamic instability and the mechanism of flutter, NACA report No. 496, Washington, pp. 413-433.

[14]. Theodore Theodorsen, I. E. Garrick (1942), Nonstationary flow about a wing-aileron-tab combination concluding aerodynamic balance, NACA report, No. 736, Washington, pp. 129-138.