Phân tích động lực học hệ liên hợp tấm - dây - cột chịu tác dụng của lực khí động

PGS. TS. Nguyễn Thái Chung ThS. Nguyễn Chiến Thắng Học viện Kỹ thuật Quân sự ThS. Vũ Anh Tuấn Trường Đại học Công nghệ GTVT Người phản biện: GS. TSKH. Nguyễn Tiến Khiêm GS. TS. Hoàng Xuân Lượng

Tóm tắt: Bài báo trình bày thuật toán phần tử hữu hạn (PTHH) và một số kết quả phân tích động lực học của hệ liên hợp tấm - dây - cột chịu tác dụng của lực khí động. Sử dụng mô hình lực khí động Scanlan, các tác giả thiết lập hệ phương trình vi phân mô tả dao động của hệ và áp dụng phương pháp tích phân trực tiếp Newmark, lập trình trong môi trường Ansys để giải. Tính toán trên ví dụ số cho thấy khả năng của thuật toán, chương trình đã lập và khảo sát số trên nhiều lớp bài toán khác nhau, làm cơ sở lựa chọn các thông số hợp lý cho hệ liên hợp tấm - dây - cột chịu tác dụng của lực khí động, làm cơ sở khoa học phục vụ tính toán, thiết kế các công trình GTVT như cầu dây văng.

Từ khóa: Hệ liên hợp tấm - dây - cột, lực khí động.

Abstract: This paper presents a finite element algorithm (FEM ) and some analysis of the system dynamics conjugate plate - Wire - column under the effect of aerodynamic forces. Use Scanlan aerodynamic model, the authors set up differential equations describing the system oscillator and apply direct integration method Newmark, environmental programming in ANSYS to solve. Calculated on the example shows the ability of the algorithm, the program was established and examined the problem on many different layers, as a basis for selecting the appropriate parameters for conjugate system plate - Wire - columns bear the effect of aerodynamic forces, as a basis for calculating serving science, design of transportation projects, such as a cable-stayed bridge.

Keywords: Complex Systems plate - Wire - columns, aerodynamic forces.

1. Mở đầu

Do sự phức tạp trong tính toán nên đến nay, khi nghiên cứu các kết cấu cầu dây văng thường được được mô hình hóa như là hệ liên hợp dầm - dây - cột [2],[5],[8]. Đây là mô hình khá đơn giản, không xem xét đến tính chất xoắn của cầu khi chịu tác dụng của tải trọng lệch tâm và trong chừng mực nào đó chưa thể hiện sát thực sự làm việc của hệ. Trong xu thế phát triển của phương pháp và phương tiện tính như hiện nay, mô hình không gian cho kết cấu dạng này đã bắt đầu xuất hiện và dần được ứng dụng rộng rãi, đặc biệt trong phân tích trạng thái chịu lực của hệ chịu lực khí động. Theo đó, kết cấu mặt cầu được mô hình hóa là dạng tấm chịu uốn thay thế cho dầm chịu uốn phẳng như trong mô hình vẫn sử dụng. Trong bài báo, các tác giả xây dựng thuật toán, chương trình phân tích động lực học hệ liên hợp tấm - dây - cột (mô phỏng kết cấu cầu dây văng theo mô hình không gian) chịu tác dụng của lực khí động do dòng khí chuyển động với vận tốc U gây nên. Trong đó, xây dựng phương trình vi phân dao động của hệ trên cơ sở xây dựng các ứng xử của phần tử tấm chịu lực khí động, xây dựng ma trận các phần tử dây cable, cột.

2. Mô hình bài toán và các giả thiết

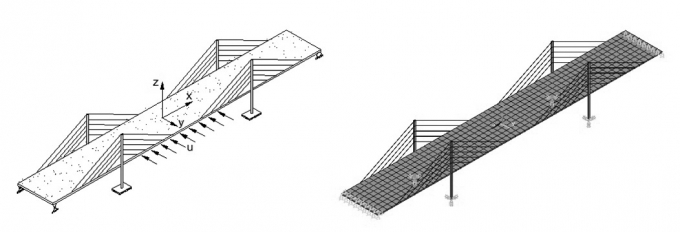
Xét hệ liên hợp tấm - dây - cột chịu tác dụng của lực khí động do dòng khí có vận tốc U chuyển động theo phương ngang gây nên. Mô hình bài toán như Hình 2.1.

a) - Mô hình thực                                                                     b) - Mô hình PTHH Hình 2.1: Mô hình bài toán

Bài toán được giải quyết trên cơ sở các giả thiết: Vật liệu của kết cấu đàn hồi tuyến tính, cột liên kết cứng với nền, tấm được xem là tấm mỏng, tuân thủ định luật Kirchhoff - Love. Xem rằng lực khí động chỉ tác dụng lên tấm, còn ảnh hưởng của nó đến các phần tử dây, cột xem như bé, được bỏ qua.

3. Thiết lập thuật toán PTHH phân tích bài toán

3.1. Phần tử dây cable [5],[8]

Phần tử dây cable đàn hồi bị kéo trong mặt phẳng thẳng đứng được biểu thị như trên Hình 3.1, với chiều dài trước khi bị kéo L_u, mô-đun đàn hồi vật liệu E, diện tích thiết diện A, trọng lượng trên một đơn vị chiều dài trước khi bị kéo là w.

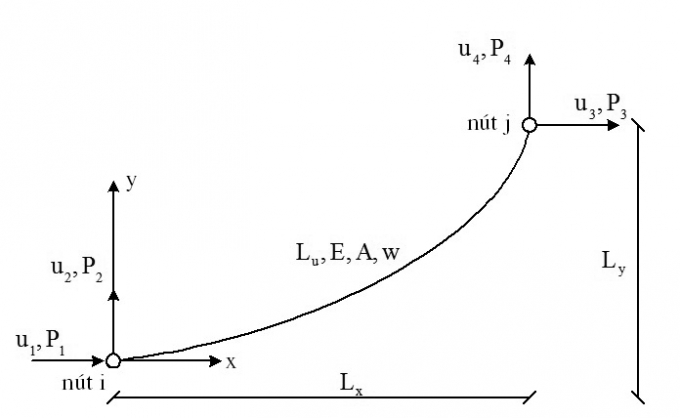Hình 3.1: Phần tử dây cable

 

Đối với dây đàn hồi, quan hệ giữa các hình chiếu và các thành phần lực tại các đầu mút phần tử là:

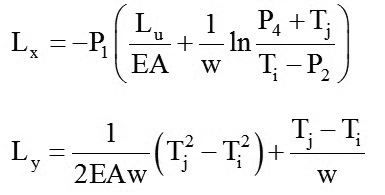         (1)

 

 

          (2)

 

 

Trong đó: T_i, T_j - Các lực kéo tại 2 nút phần tử

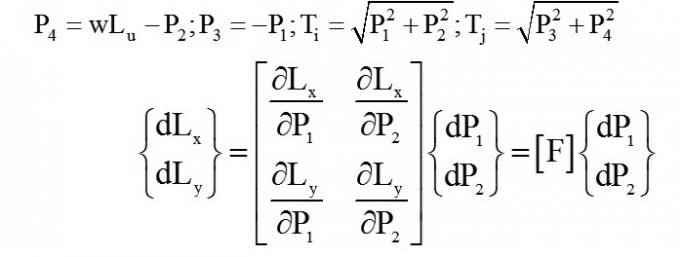Ta có [1]:

Ta có [1]: 

 

(3)

 

 

 

 

Trong đó: [F] - Ma trận độ mềm.

Ma trận độ cứng tiếp tuyến [K_t] và véc-tơ nội lực tương ứng của phần tử 4 bậc tự do tại nút có dạng:

 

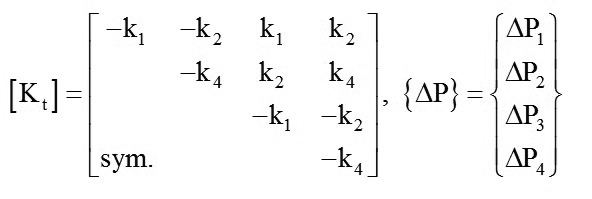     (4)

 

 

 

Ma trận [K_t] là hệ thức liên hệ giữa véc-tơ số gia lực nút của {∆P₁,∆P₂, ∆P₃, ∆P₄}^T và véc-tơ số gia chuyển vị nút của phần tử {∆u₁,∆u₂, ∆u₃, ∆u₄}^T. Ma trận [K_t] và các lực nút P₁, P₂ cần được tính đầu tiên. Các lực này xem như đã biết tuỳ theo vị trí ban đầu của các nút phần tử cable, được sử dụng cho quá trình lặp độ cứng. Quá trình này đòi hỏi phải biết các giá trị ban đầu của các lực P₁,P₂. Việc xác định ma trận độ cứng của dây cable được thực hiện theo phương pháp lặp.

3.2. Phần tử cột [9]

Phần tử cột ở đây được hiểu như là trường hợp phần tử dầm không gian 2 điểm nút, mỗi nút có 6 bậc tự do. Mô hình và các bậc tự do của phần tử thể hiện như trên Hình 3.2.

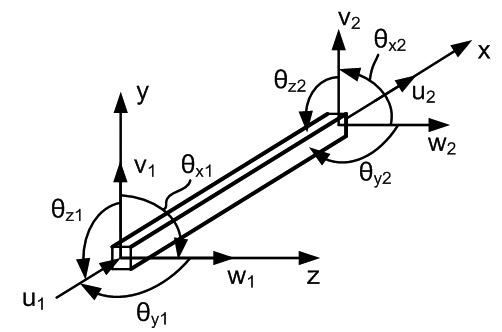Hình 3.2: Phần tử cột

 

Véc-tơ chuyển vị nút của phần tử:

       (5)

 

 

Như vậy, trong trường hợp này, mỗi phần tử cột có 12 bậc tự do. Quan hệ nội lực và biến dạng của cột:                              

      (6)

 

 

Ma trận độ cứng, ma trận khối lượng phần tử cột cấp (12´12) được xác định theo [4],[9].

3.3. Lực khí động tác dụng lên phần tử tấm

Khi chịu tác dụng của luồng gió, trong mô hình PTHH của kết cấu, mỗi phần tử tấm phẳng chịu tác dụng của lực nâng phân bố L_w và mô-men uốn phân bố M_w, gọi chung là lực khí động tác dụng lên phần tử tấm phẳng, chúng được xác định [1], [9]:

 

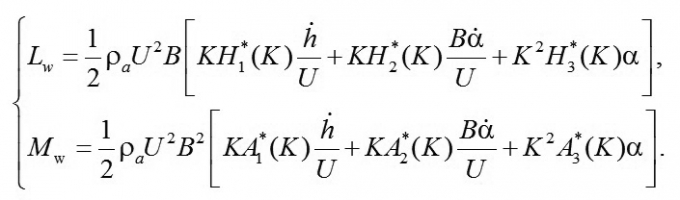(7)

 

 

 

 

Trong đó: p - Mật độ không khí; U - Vận tốc dòng khí; B - Bề rộng phần tử theo phương gió tác dụng; K - Tần số thu gọn và                                     

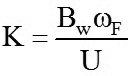      (8)

      

Các hàm A_ι*(K),H_ι* (K) với i = 1 ¸ 3, được xác định bởi:

 

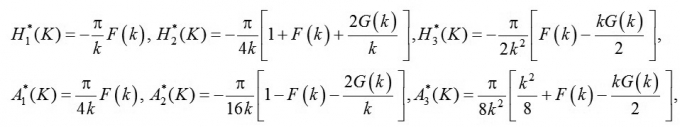  (9)

 

 

với k = K/2, các hàm F(k), G(k) được xác định bởi:                        

 

(10)

 

 

3.4. Phương trình dao động phần tử tấm chịu lực khí động

Dưới tác dụng của lực khí động và tải trọng khác, áp dụng nguyên lý Hamilton cho phần tử [2],[4],[9]:

 

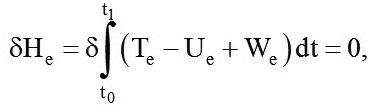   (11)

 

Trong đó: He = T_e - U_e + W_e = H_e({q^e}, {`dotq` ^e}  ,t) - Hàm tác dụng Hamilton; T_e - Động năng của phần tử; U_e - Thế năng toàn phần của phần tư; W_e - Công gây ra bởi ngoại lực tác động lên phần tử; {q^e}, { `dotq` ^e}  - Tương ứng là véc-tơ chuyển vị, vận tốc nút của phần tử.

Ta có phương trình vi phân mô tả dao động của phần tử tấm như sau:

 

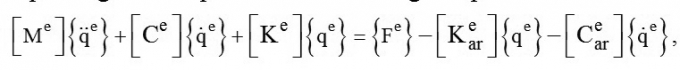  (12)

Trong đó:  [ C^e_ar] ,  [ K^e_ar]- Tương ứng là ma trận cản khí động, ma trận độ cứng khí động của phần tử, được xác định như trong [1],[9]; {F^e} - Tải trọng trọng nút của phần tử không liên quan đến lực khí động.

Viết lại (12) dưới dạng sau:

 

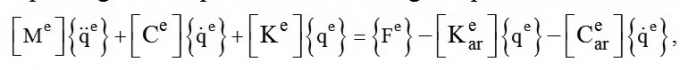   (13)

Trường hợp tấm chỉ chịu tác dụng của lực khí động, phương trình (13) trở thành:

  (14)

 

3.5. Thuật toán PTHH giải bài toán

Việc ghép nối các phần tử tấm, phần tử cột và phần tử dây (cable) tạo thành mô hình PTHH tổng thể của hệ được thực hiện bằng phương pháp độ cứng trực tiếp và sơ đồ Skyline theo thuật toán chung của phương pháp PTHH [3],[4],[7]. Sau khi ghép nối xây dựng các ma trận, véc-tơ tổng thể và khử biên, ta có phương trình vi phân mô tả dao động của hệ liên hợp tấm - dây - cột chịu tác dụng của lực khí động xuất phát từ phương trình (13) như sau:

     (15)

 

Hay:                                                             

   (16)

 

Trong đó:

 

     

[M^e_s],[K^e_s]- Tương ứng là các ma trận khối lượng phần tử, ma trận độ cứng phần tử của kết cấu (không liên quan đến lực khí động). Các hằng số cản Rayleigh a_r, b_r được xác định thông qua tỷ số cản x và hai tần số dao động riêng đầu tiên của kết cấu [9].

Các tác giả sử dụng phương pháp tích phân trực tiếp Newmark để giải phương trình (16) và cụ thể hóa thuật toán bằng việc lập trình tính toán trong môi trường Ansys, chương trình có tên Cable_Bridge_Aerodynamic. Chương trình tính đã được kiểm chứng và đảm bảo độ tin cậy.

4. Ví dụ số

Thông số kết cấu: Hệ liên hợp tấm - dây - cột, trong đó tấm bằng vật liệu bê tông, chiều dài L_p = 150m, chiều rộng W_p = 12m, chiều dày h = 0,10m, mô-đun đàn hồi E = 3,4.10¹⁰N/m², hệ số Poisson n = 0,3, khối lượng riêng r = 2500kg/m³. Hệ gồm 3 nhịp, có 4 cột bằng bê tông, mặt cắt ngang chữ nhật b_y ´ b_x = 0,3m ´ 0,4m, chiều dài tổng cộng H = 35m, phần từ mặt tấm đến mặt nền có chiều dài H₁ = 20m, bố trí đối xứng. Hai dãy dây cáp bằng thép bố trí 2 bên, với 20 dây mỗi nhịp.

Thông số tải trọng: Tải trọng khí động tác dụng do dòng khí chuyển động với vận tốc U = 30m/s, tác dụng theo phương ngang.

Sử dụng chương trình đã lập, tiến hành tính toán dao động riêng và phân tích động lực học bài toán với bước tích phân Dt = 0,06s, thời gian tính là t_cal = 15s.

Điểm xuất kết quả là nút 286 (điểm chính giữa tấm). Điều kiện đầu:                         .

Kết quả tính:Hình 4.1, 4.2 tương ứng là đáp ứng chuyển vị đứng w, gia tốc chuyển vị đứng

theo thời gian tại điểm mép ngoài và điểm giữa tấm. Hình 4.3, 4.4 tương ứng là đáp ứng mô-men uốn M_x tại chân cột và lực dọc N trong dây cáp chủ theo thời gian.

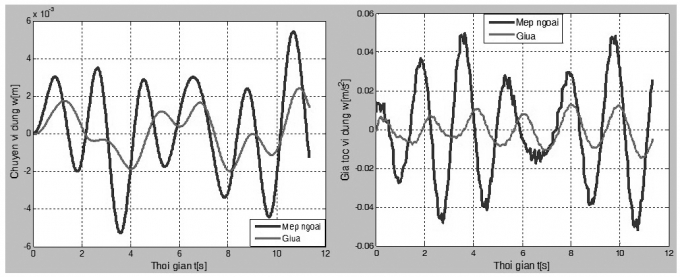Hình 4.1: Đáp ứng độ võng w - thời gian              Hình 4.2: Đáp ứng gia tốc đứng    - thời gian

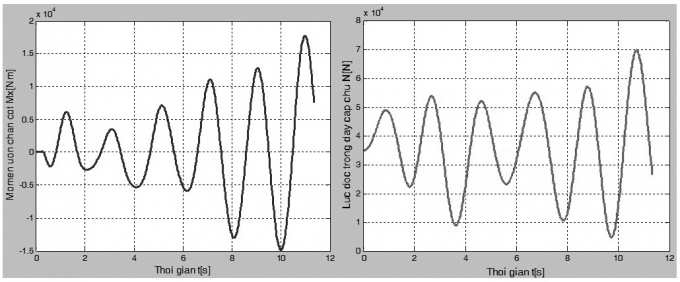Hình 4.3: Đáp ứng mô-men uốn Mx - thời gian                 Hình 4.4: Đáp ứng lực dọc N - thời gian

 

Bảng 4.1. Tóm tắt giá trị lớn nhất về chuyển vị, gia tốc, nội lực tại các điểm tính w

 

Hình 4.5, 4.6 tương ứng là đáp ứng về ứng suất s_x, s_y và đáp ứng lực dọc N_z trong cột theo thời gian.

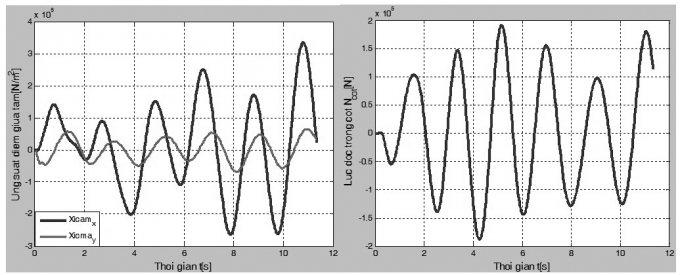Hình 4.5: Đáp ứng ứng suất - thời gian                            Hình 4.6: Đáp ứng lực dọc Nz - thời gian

Bảng 4.2. Tóm tắt giá trị lớn nhất về ứng suất trong tấm và lực dọc trong cột

 

Nhận xét: Đáp ứng động của hệ tấm - dây - cột chịu lực khí động là phức tạp, với trường hợp cụ thể của bài toán cho thấy đáp ứng chuyển vị, gia tốc đứng tại điểm tính thuộc tấm và lực dọc trong cột là ổn định, còn lực dọc trong cáp chủ và ứng suất s_x tại điểm tính thuộc tấm có xu hướng tăng theo thời gian. Điều này cho thấy khả năng ổn định của hệ là đảm bảo, song có thể dẫn đến tấm và cáp chủ bị phá hủy vì không đảm bảo điều kiện bền. 

5. Kết luận

Xây dựng các quan hệ ứng xử và thuật toán, chương trình tính phân tích động lực học hệ liên hợp tấm - dây - cột chịu tải trọng khí động, trong đó sử dụng mô hình lực khí động Scanlan.

- Khảo sát số xác định đáp ứng động động lực học (chuyển vị, gia tốc, nội lực) của hệ dưới tác dụng của lực khí động do dòng khí chuyển động với vận tốc không đổi gây ra, kết quả cho phép xem xét, phán đoán khả năng làm việc của hệ.

Kết quả nghiên cứu của bài báo là cơ sở cho việc khảo sát lựa chọn các thông số hợp lý cho một số dạng cầu dây văng chịu tác dụng của lực khí động, góp phần phát triển ngành GTVT

Tài liệu tham khảo

[1]. Trần Ngọc An (2014), Tính toán ổn định khí động flutter của dầm chủ trong kết cấu cầu hệ dây bằng phương pháp bước lặp, Luận án Tiến sĩ kỹ thuật, Trường Đại học Bách khoa Hà Nội.

[2]. Nguyễn Thái Chung, Vũ Anh Tuấn, Đỗ Ngọc Tiến (2014), Nghiên cứu giảm dao động cho hệ liên hợp tấm - dây - cột chịu tải trọng di động bằng thiết bị Tuned Mass Damper (TMD), Tuyển tập Công trình Hội nghị Cơ học kỹ thuật toàn quốc, Hà Nội.

[3]. Nguyễn Thái Chung, Bùi Văn Thắm, Dương Thị Ngọc Thu, Vũ Anh Tuấn (2012), Dao động của hệ liên hợp tấm - cột chịu tác dụng của tải trọng di động, số 147, Tạp chí Khoa học và Kỹ thuật, Học viện Kỹ thuật Quân sự, tr.14 - 23.

[4]. Chu Quốc Thắng (1997), Phương pháp phần tử hữu hạn, NXB. Khoa học và Kỹ thuật.

[5]. Phan Thanh Tuấn (2012), Phân tích động lực hệ dầm liên hợp chịu tác dụng đồng thời của tải trọng di động và lực khí động, Luận án Tiến sĩ kỹ thuật, Học viện Kỹ thuật Quân sự, Hà Nội.

[6]. Trần Thế Văn (2012), Nghiên cứu ổn định của tấm composite lớp chịu tải trọng khí động, Luận án Tiến sĩ kỹ thuật, Học viện Kỹ thuật Quân sự, Hà Nội.

[7]. Bathe K. J. and Wilson E. L. (1978), Numerical Method in Finite Method Analyis Prentice, Hall of India Private Limited, New Delhi.

[8]. M.F. Liu a, T.-P. Chang b, D.-Y. Zeng (2011), The interactive vibration behavior in a suspension bridge system under moving vehicle loads and virtical seismic excitations, Applied Mathematical Modelling 35(2011), pp.398-411.

[9]. Ansys Inc.Theory reference, Southpointe 275 Technology Drive Canonsburg, 2010.