Phát triển mô hình động lực học theo phương dọc của lốp trên cơ sở mô hình Pacejka

TS. Trần Văn Như Trường Đại học Giao thông vận tải ThS. Đinh Quang Vũ TS. Đặng Việt Hà Cục Đăng kiểm Việt Nam ThS. Nguyễn Hữu Mạnh Trường Cao đẳng Lý Tự Trọng Người phản biện: GS. TSKH. Phạm Văn Lang PGS. TS. Cao Trọng Hiền

TÓM TẮT: Mô hình động lực học tương tác giữa lốp và mặt đường theo phương dọc có ý nghĩa quan trọng cho việc nghiên cứu phát triển các hệ thống điều khiển động lực học ô tô theo phương dọc như hệ thống chống bó cứng bánh xe khi phanh, hệ thống điều khiển kéo. Mô hình lốp Pacejka là mô hình phi tuyến mô tả rất tốt đặc tính bám của lốp, tuy nhiên đó là mô hình tĩnh, bởi vậy không phù hợp để phát triển các hệ thống điều khiển động lực học theo phương dọc. Bài báo tập trung phát triển một mô hình động lực học của lốp theo phương dọc trên cơ sở mô hình Pacejka. Một vài kết quả mô phỏng được đưa ra để cho thấy hiệu quả của mô hình.

TỪ KHÓA: Mô hình động lực học lốp theo phương dọc, tương tác giữa lốp và đường, mô hình Pacejka.

ABSTRACT: Longitudinal tyre dynamics model of interacting with road is important to developing the longitudinal dynamic control systems such as the anti-lock braking systems, traction control systems. The Pacejka’s tyre model is a nonlinear model describing well the characteristics of tyre-road interaction. However, that is the static model and therefore not suitable to develop the longitudinal dynamic control systems. This paper focus on developing a longitudinal tyre dynamics model based on the Pacejka’s tyre model. Several simulation results are provided to show the efficiency of developed model.

Keywords: Longitudinal tyre dynamic model, tyre-road interaction, Pacejka’s tyre model.

1. ĐẶT VẤN ĐỀ

Lốp xe là một trong những bộ phận quan trọng, nó không chỉ góp phần tạo ra chuyển động mà còn là bộ phận ảnh hưởng đến an toàn chuyển động của ô tô. Khi ô tô chuyển động trên đường, tại vị trí lốp xe tiếp xúc với mặt đường có các thành phần lực tương tác giữa chúng. Các thành phần lực này tác dụng lên lốp, gây ảnh hưởng đến quỹ đạo chuyển động của ô tô, có thể gây mất an toàn khi ô tô chuyển động ở các tốc độ cao. Đây là một vấn đề đã và đang nhận được sự quan tâm của các tác giả trong nước cũng như trên thế giới.

Liên kết giữa lốp - mặt đường là yếu tố quan trọng quyết định đến động lực học của ô tô theo 3 phương: Phương thẳng đứng, phương dọc và phương ngang. Trong đó, theo phương thẳng đứng, lốp xe có tác dụng nâng đỡ toàn bộ khối lượng của ô tô đồng thời ảnh hưởng trực tiếp đến các tính chất dao động của ô tô. Theo phương dọc và phương ngang, liên kết lốp - mặt đường có ảnh hưởng quyết định đến tính chất kéo, tính chất phanh và tính ổn định hướng chuyển động của ô tô.

Mô hình lực tương tác giữa bánh xe và mặt đường, đặc biệt là mô hình lực dọc và lực ngang có ý nghĩa quan trọng trong việc mô phỏng động lực học ô tô theo phương dọc/ngang, thiết kế các bộ điều khiển cho hệ thống nâng cao ổn định quỹ đạo chuyển động của ô tô, các bộ điều khiển động học theo phương dọc của ô tô như ABS, TRC…

Trên thế giới có nhiều công trình nghiên cứu mô hình hóa các thành phần lực tương tác giữa bánh xe và mặt đường, đặc biệt lực tương tác theo phương dọc và ngang điển hình như trong [1] đã xây dựng mô hình toán lực dọc, ngang và mô-men cản quay của lốp xe, được gọi tên là mô hình Pacejka, tuy nhiên các mô hình này là mô hình tĩnh phụ thuộc tương ứng vào hệ số trượt, góc lăn lệch của bánh xe. Mô hình này là mô hình phi tuyến, tuy nhiên chỉ có ý nghĩa cho việc mô phỏng động lực học ô tô ở trạng thái ổn định, chưa mô phỏng được động lực học trạng thái quá độ của bánh xe đặc biệt ở trạng thái khởi hành và trạng thái giới hạn trượt dọc. Bản chất lực tương tác theo phương dọc/ngang giữa bánh xe và mặt đường là lực ma sát. Liên quan đến mô hình ma sát, trên thế giới có nhiều tác giả xây dựng mô hình ma sát cho phục vụ thiết kế điều khiển hệ thống như [2] đề xuất mô hình LuGre và sử dụng mô hình LuGre để xây dựng mô hình động lực học lực tương tác giữa bánh xe và mặt đường theo phương dọc [3], phương dọc và phương ngang kết hợp [4]. Tuy nhiên, mô hình LuGre làm việc không hiệu quả khi phản lực thẳng đứng thay đổi [5].

Trong nghiên cứu này, các tác giả phát triển mô hình động lực học lực tương tác giữa lốp với mặt đường theo phương dọc trên cơ sở mô hình Pacejka và mô hình “bàn chải”  mô tả động lực học ma sát giữa 2 bề mặt.

2. MÔ HÌNH ĐỘNG LỰC HỌC LỰC TƯƠNG TÁC THEO PHƯƠNG DỌC GIỮA BÁNH XE VÀ MẶT ĐƯỜNG

2.1. Mô hình Pacejka

Pacejka đã tìm ra biểu thức toán học mô tả đặc tính bám của lốp xe với mặt đường trong công trình [1] như sau:

 

 

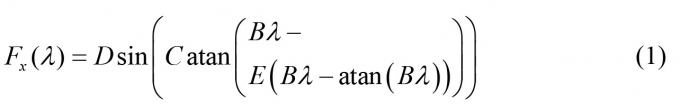Trong đó: B, C, D, E - Các đại lượng đặc trưng của đường cong lực bám F_x(λ) . Các đại lượng này phụ thuộc vào phản lực thẳng đứng F_z và 9 hệ số a₀ , a₁ , a₂ ,...,a₈ . Thông số C = a₀ ảnh hưởng đến giá trị lực bám dọc ở trạng thái trượt hoàn toàn (λ = 100%). 

 

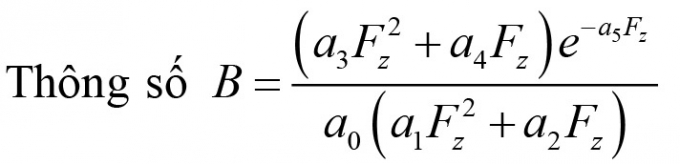 ảnh hưởng đến giá trị đỉnh của đường đặc tính, tương ứng với giá trị lực bám dọc đạt cực đại. Thông số  ảnh hưởng đến độ cứng dọc của lốp. Độ cứng dọc của lốp C_x được xác định như sau:

 

 

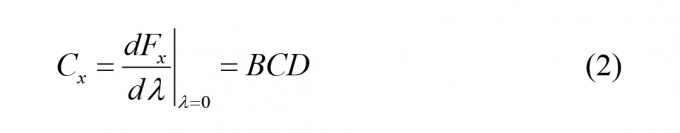Thông số E = a₆ F_z² +a₇ F_z + a₈ ảnh hưởng đến hình dáng cong của đường đặc tính bám. λ - Hệ số trượt dọc, được xác định theo biểu thức:

 

 

Trong đó: ω - Vận tốc góc của bánh xe; V_x- Vận tốc dài tại tâm bánh xe; r_bx - Bán kính làm việc trung bình của bánh xe.

Hình 2.1 thể hiện hình dạng đường cong (1) phụ thuộc vào các tham số.

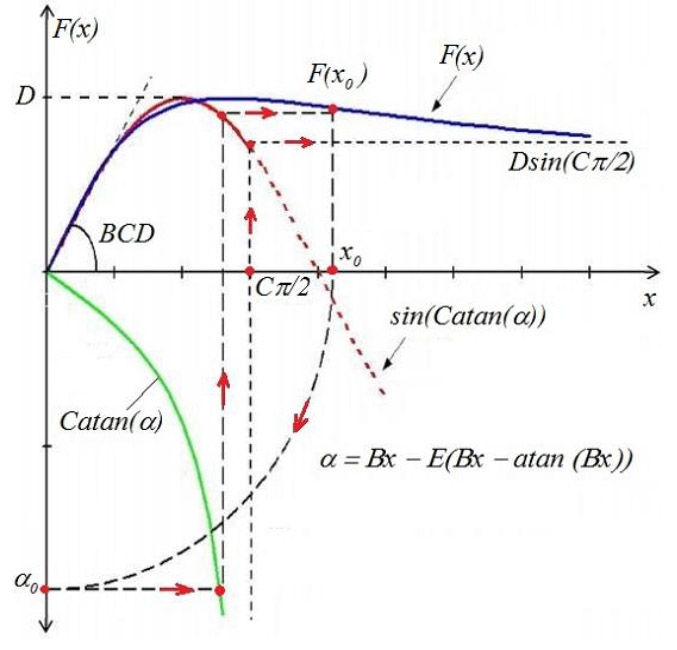Hình 2.1: Hình dáng đường cong Pacejka

2.2. Mô hình động lực học liên kết giữa bánh xe và mặt đường theo phương dọc

Xem xét mô hình bánh xe chịu mô-men kéo (hoặc phanh) M. Mô hình hóa liên kết giữa bánh xe và mặt đường bằng các “lông cứng” (mô hình bàn chải). Không mất tổng quát khi xét mô hình có một “lông cứng” có độ cứng tổng cộng theo phương dọc C_x như Hình 2.2. Độ cứng dọc của lốp tương ứng với độ cứng của “lông cứng”.

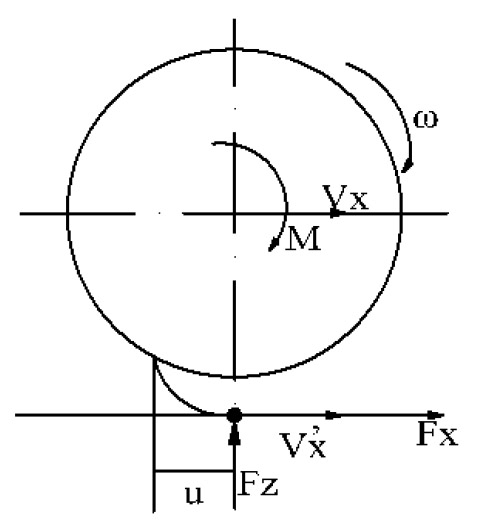Hình 2.2: Mô hình động lực liên kết lốp với mặt đường

Các lực tương tác giữa bánh xe và mặt đường gồm: Phản lực thẳng đứng F_z; phản lực dọc F_x . Phản lực F_z phụ thuộc vào trọng lượng phân bố lên bánh xe và lực động tương tác giữa bánh xe và mặt đường. Thành phần phản lực F_z quyết định đến độ lớn lực dọc F_x. Bánh xe quay với vận tốc góc ω và vận tốc dài tại tâm bánh xe V_x  so với hệ trục cố định gắn trên đường. Vận tốc dài tại điểm tiếp xúc giữa “lông cứng” với mặt đường so với hệ trục cố định gắn trên đường ký hiệu V'_x. Khi chịu lực dọc F_x “lông cứng” bị biến dạng u theo phương dọc. Nếu lực F_x lớn gây ra sự trượt giữa đầu “lông cứng” với mặt đường.

Khi không có mô-men tác dụng, do đó “lông cứng” không bị biến dạng dọc, lốp xe lăn không trượt. Mối quan hệ giữa vận tốc góc và vận tốc dài tại tâm bánh xe:

 

 

Trong đó: r_bx - Bán kính bánh xe.

Khi có mô-men tác dụng nếu giả thiết độ cứng theo phương dọc là rất lớn (“lông cứng” cứng tuyệt đối), khi đó, “lông cứng” không biến dạng, lốp lăn có trượt với vận tốc trượt tương đối được xác định theo biểu thức:

 

Trong thực tế, lốp có độ đàn hồi theo phương dọc, vận tốc trượt tương đối khi này là hiệu giữa vận tốc trượt khi “lông cứng” không biến dạng và vận tốc biến dạng của “lông cứng”. Vận tốc trượt tổng cộng V'_x khi đó được xác định:

 

 

Hệ số trượt trong trường hợp tổng quát được xác định:

 

 

Từ biểu thức (6) và (7) ta có:

 

 

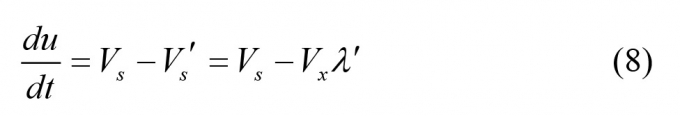Lực tương tác dọc phụ thuộc vào độ cứng dọc của lốp và độ biến dạng của “lông cứng”. Giả sử độ cứng dọc của lốp là hằng số, lực tương tác dọc được xác định theo công thức:

 

 

Với độ cứng dọc của lốp C_xđược xác định theo công thức:

 

 

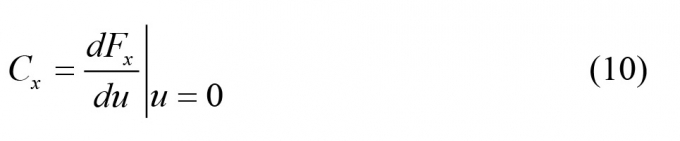Từ (9) đạo hàm 2 vế theo thời gian ta có:

 

 

 

 

 

 

 

 

Xét trong trạng thái giới hạn trượt, coi F_x  phụ thuộc tuyến tính vào λ' (Hình 2.1), F_x = C_xλ' và xét F_z  không thay đổi theo thời gian, từ (15) ta có:        

 

 

Phương trình (15) và (16) là phương trình vi phân mô tả động lực học liên kết giữa bánh xe với mặt đường (hệ số trượt).

2.3. Mô hình động lực học bánh xe theo phương dọc

Bỏ qua thành phần lực cản lăn ta có mô hình động lực học theo phương dọc của bánh xe thể hiện trên Hình 2.3.

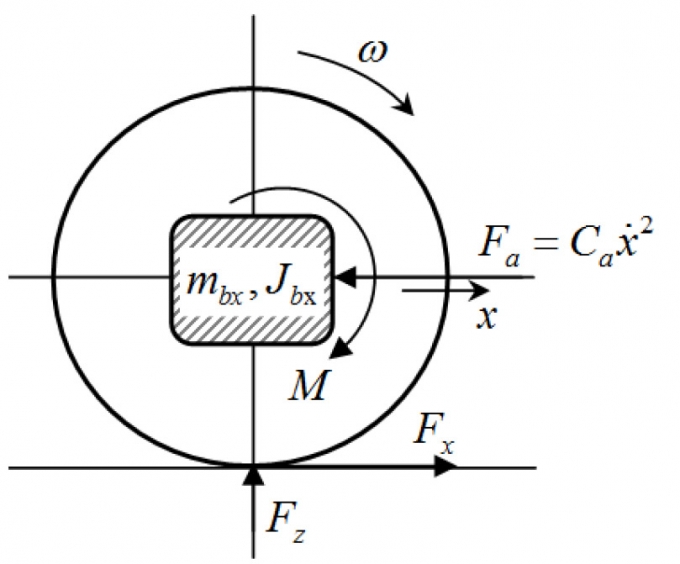Hình 2.3: Mô hình động lực học bánh xe theo phương dọc

Trong đó: m_bx - Khối lượng của ô tô trên một bánh xe;  J_bx - Mô-men quán tính khối của bánh xe; C_a - Hệ số cản không khí của ô tô phân bổ cho 1 bánh xe. Hệ có 2 tọa độ suy rộng là góc quay ω và dịch chuyển theo phương dọc x của bánh xe.

Áp dụng nguyên lý D’Alambert ta có:

 

 

 

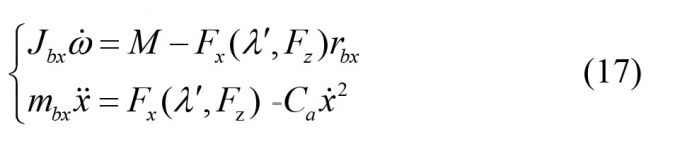Trong đó: F_z - Phản lực thẳng đứng tương tác giữa bánh xe và mặt đường. F_x  xác định theo (1) và (15) hoặc (16) trong trường hợp đơn giản hóa.

 3. MÔ PHỎNG ĐỘNG LỰC HỌC LỐP THEO PHƯƠNG DỌC

Trên Hình 3.1 là kết quả thí nghiệm đặc tính bám dọc của lốp [6]

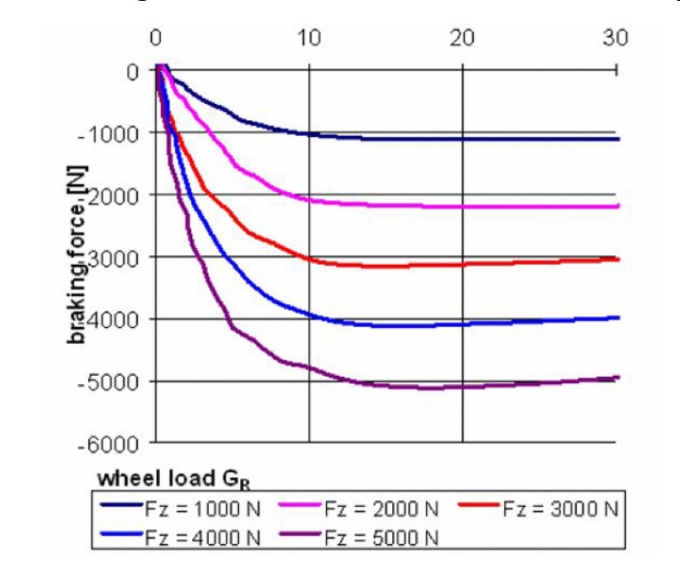Hình 3.1: Kết quả thí nghiệm đặc tính bám dọc của lốp 195/50R15 [6]

 Từ đường đặc tính thí nghiệm Hình 3.1, ta xác định được bộ thông số cho mô hình Pacejka:

 

 

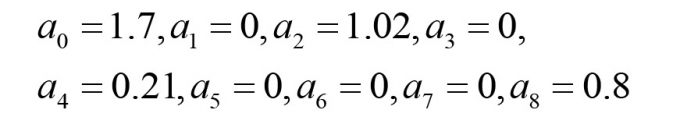Trên Hình 3.2 là đường đặc tính bám dọc của lốp theo mô hình Pacejka với bộ thông số trên, phản lực thẳng đứng tác dụng lên bánh xe F₂= 2.500N.

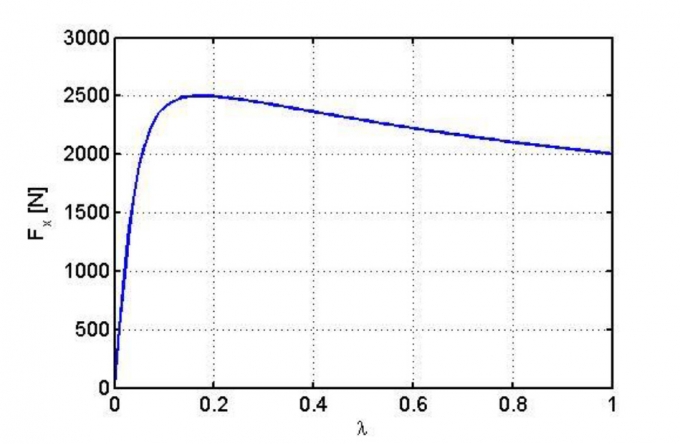Hình 3.2: Đặc tính lực bám dọc của lốp với phản lực thẳng đứng F2 = 2.500N

 Trên Hình 3.3 thể hiện sơ đồ mô phỏng được xây dựng bằng phần mềm Matlab/Simulink.

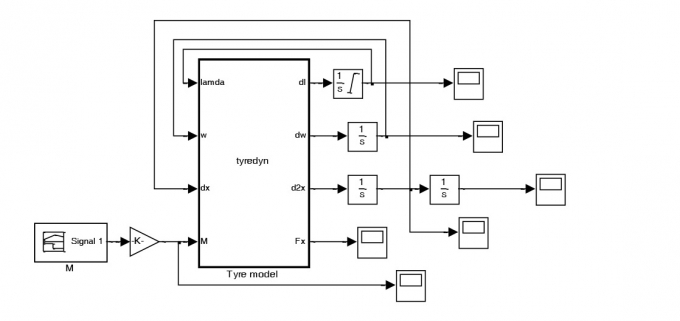Hình 3.3: Sơ đồ mô phỏng động lực học bánh xe theo phương dọc

 

Thông số đầu vào của mô hình là mô-men M tại trục của bánh xe. Thông số của mô hình như sau: Mô-men quán tính của bánh xe J_bx= 3,6kgm²; khối lượng của ô tô trên một bánh xe m_bx = 250kg; hệ số cản của ô tô trên một bán xe C_a= 0,5Ns²/m². Coi lực F_z không thay đổi theo thời gian, F_z = m_bxg với g là gia tốc trọng trường. Điều kiện ban đầu: X(0) =0; ω   (0) = 0; λ'(0) = 0.

Trong trường hợp bánh xe tiếp nhận mô-men kéo M thay đổi theo thời gian thể hiện trên Hình 3.4. Mô-men kéo tăng dần tuyến tính, đạt cực đại và giữ không đổi ở giá trị cực đại 1.000Nm.

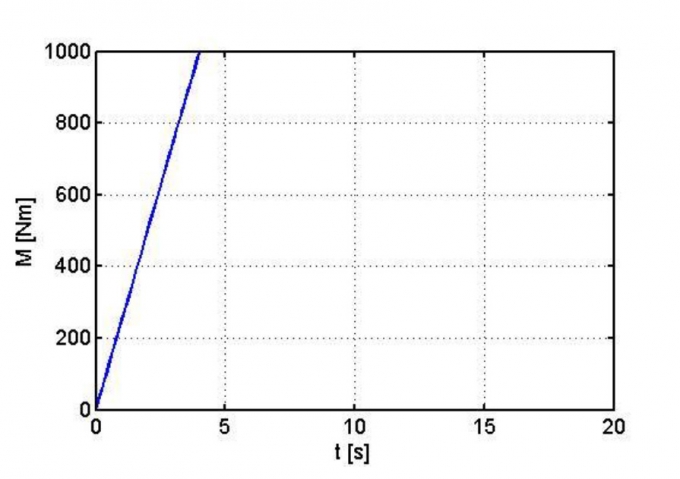Hình 3.4: Mô-men kéo thay đổi theo thời gian

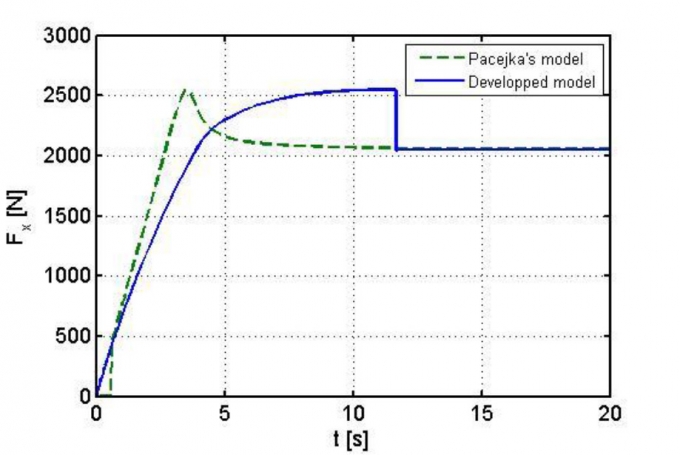
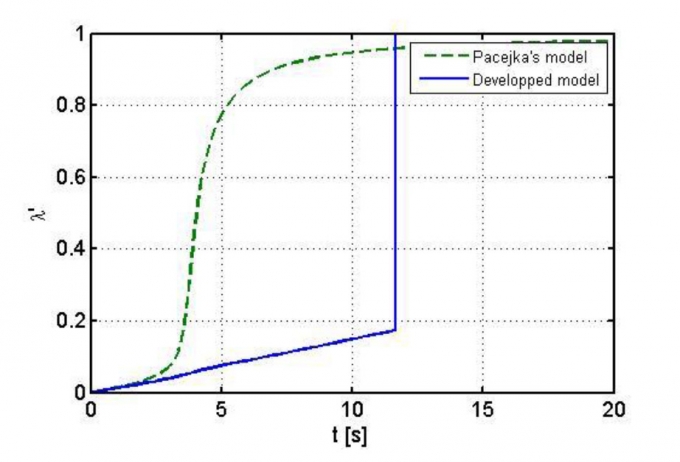
Hệ số trượt tương đối giữa bánh xe và mặt đường thể hiện trên Hình 3.5 và lực kéo F_x thể hiện trên Hình 3.6. Trên Hình 3.5, tại thời điểm t = 11,65s, lực kéo F_x  đạt giá trị lớn nhất F_xmax = 2.550N, tương ứng với hệ số trượt λ'₀ = 0,175 (Hình 3.6) và λ' tăng nhanh về 1, bánh xe trượt hoàn toàn, lực dọc giảm đột ngột về khoảng 2.045N.

Trong khoảng thời gian từ 0s khoảng 4s sự tăng lực dọc tuyến tính tương ứng với hệ số trượt nhỏ hơn 0,075.

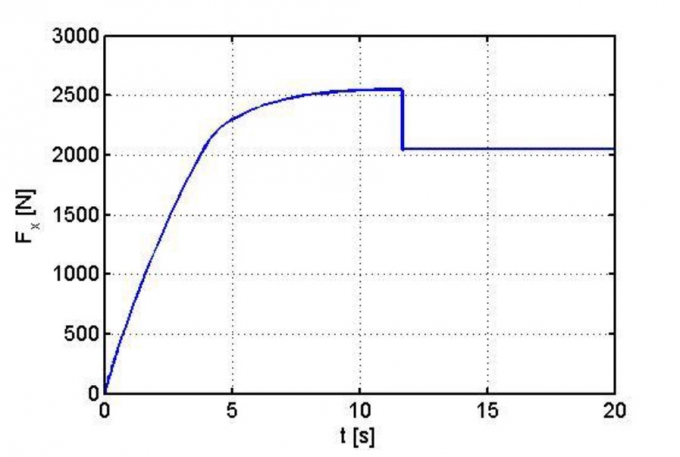Hình 3.5: Lực dọc thay đổi theo thời gian

 

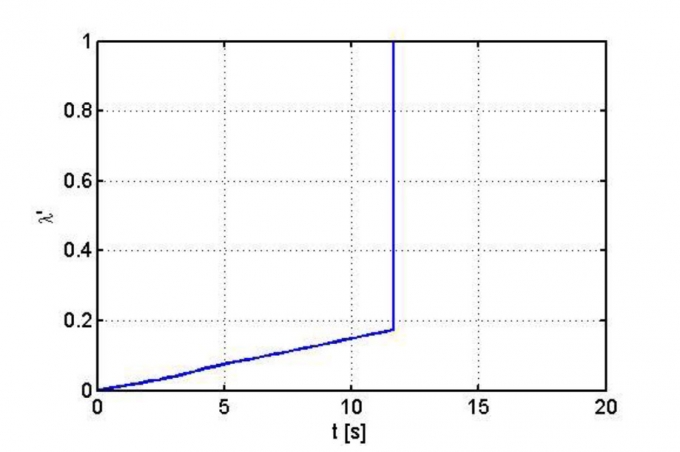Hình 3.6: Hệ số trượt λ'thay đổi theo thời gian

Giai đoạn này là giai đoạn ổn định trượt. Trong khoảng thời gian từ 4s đến 11,65s, tương ứng với hệ số trượt trong khoảng 0,075 đến 0,175, sự gia tăng lực dọc là phi tuyến, giai đoạn này là giai đoạn giới hạn ổn định trượt. Khi  t > 11,65s, sự trượt xảy ra hoàn toàn.

Trên Hình 3.7 và Hình 3.8 tương ứng thể hiện so sánh đáp ứng của lực dọc và hệ số trượt giữa mô hình Pacejka và mô hình phát triển. Đối với mô hình Pacejka, để tránh chia cho 0 khi tính hệ số trượt theo (3), điều kiện ban đầu thực hiện mô phỏng X(0) =0.31*10^-6; ω(0) = 10^-6; λ'(0) = 0.

Hình 3.7: So sánh đáp ứng lực dọc theo thời gian

Hình 3.8: So sánh đáp ứng hệ số trượt theo thời gian

Trong giai đoạn ổn định, hệ số trượt nhỏ hơn 0,075 sự sai khác lực dọc giữa mô hình phát triển và mô hình Pacejka không nhiều. Tuy nhiên, trong giai đoạn giới hạn ổn định trượt dọc, hệ số trượt trong khoảng 0,075 đến 0,175, tương ứng thời gian mô phỏng khoảng từ 4s đến 11,65s thì sự khác biệt giữa 2 mô hình là đáng kể. Đối với mô hình Pacejka, khi lực dọc đạt giá trị cực đại thì sẽ giảm dần theo thời gian. Tương tự như vậy, đối với hệ số trượt (Hình 3.8), khi hệ số trượt đạt đến giá trị  λ'₀ mà ở đó lực dọc là lớn nhất thì sẽ trượt nhanh về 1 (trượt hoàn toàn), điều này là phù hợp với thực tế. Với mô hình Pacejka thì hệ số trượt đạt đến λ'₀ thì tiếp tục tăng nhanh và tiệm cận đến 1, điều này là không phù hợp với thực tế vì một khi lực kéo bằng giá trị lực bám cực đại (tại λ'₀ ) thì lực bám sẽ giảm, dẫn đến lực kéo lớn hơn lực bám do đó sẽ trượt hoàn toàn.

Trong các trường hợp mô phỏng, ở trạng thái ban đầu, mô-men kéo bằng 0, vận tốc dài và góc của bánh xe bằng 0. Trong các giai đoạn quá độ này, mô hình xây dựng làm việc vẫn ổn định. Khi mô-men kéo tăng dần thì hệ số trượt cũng tăng dần từ 0, vận tốc góc và dài của bánh xe cũng tăng dần từ 0. Khi sử dụng mô hình tĩnh để xác định độ trượt thì trong trường hợp quá độ này độ trượt không xác định được do chia cho 0. Để tránh hiện tượng này thì cần phải khai báo điều kiện vận tốc góc và dài của bánh xe ban đầu khác không.

5. KẾT LUẬN

Các tác giả đã xây dựng mô hình động lực học lực tương tác giữa bánh xe với mặt đường trên cơ sở mô hình hóa sự tiếp xúc giữa bánh xe với mặt đường bằng mô hình “bàn chải” được đặc trưng bằng các liên kết “lông cứng”. Trên cơ sở mô hình hóa, các tác giả đã xây dựng phương trình vi phân của hệ số trượt tương đối giữa bánh xe với mặt đường. Sử dụng công thức Pacejka để mô tả đặc tính lực bám phụ thuộc vào hệ số trượt.

Hệ số trượt được xác định bằng cách giải phương trình vi phân giúp mô tả đáp ứng động lực học lực tương tác giữa bánh xe với mặt đường trong giai đoạn quá độ như khi bắt đầu truyền mô-men kéo hoặc ở trạng thái giới hạn trượt.

Kết quả mô phỏng cho thấy sự làm việc ổn định trong giai đoạn quá độ, kết quả mô phỏng phản ánh đúng bản chất bám giữa bánh xe với mặt đường ở giai đoạn quá độ cũng như giai đoạn ổn định. Bài báo chỉ dừng lại ở mô phỏng trên máy tính, cần có các nghiên cứu thực nghiệm để khẳng định sự chính xác của mô hình nghiên cứu.

Tài liệu tham khảo

[1]. H. B. Pacejka (2006), Tyre and Vehicle Dynamics, Butterworth-Heinemann.

[2]. C. Canudas de Wit, H.Olsson, K.J.Astrom and P.Lischinsky (1995), A new model for control of systems with friction, IEEE Trans. Autom. Control, vol 40, tr 419-424.

[3]. C. Canudas-de-Wit, M. Lind Petersen and A. Shiriaev (2003), A New Nonlinear Observer for Tire/Road Distributed Contact Friction, Conf. Decis. Control.

[4]. E. Velenis, P. Tsiotras, C. Canudas-De-Wit and M. Sorine (2005), Dynamic tyre friction models for combined longitudinal and lateral vehicle motion, Veh. Syst. Dyn., vol 43, s.1, pp. 3-29.

[5]. R. Nouailletas (2009), Modélisation hybride, identification, commande et estimation d’états de système soumis à des frottements se cs - Application à un embrayage robotisé, Grenoble INP, Grenoble.

[6]. P. Holdmann, P. Kohn and J. Holtschulze (7/1999), Dynamic tyre properties under combined slip situation in test and simulation, Eur. Automot. Congr.