Phương pháp xác định tải trọng giới hạn của tấm tựa khớp theo hai định lý giới hạn

ThS. Mai Thị Hải Vân Trường Ðại học Công nghệ Giao thông vận tải Người phản biện: TS. Nguyễn Thùy Anh PGS. TSKH. Hà Huy Cương.

TÓM TẮT: Bài báo giới thiệu các khái niệm và hai định lý cơ bản của lý thuyết phân tích giới hạn, sau đó trình bày một vài ví dụ xác định tải trọng giới hạn của tấm có chu vi tựa khớp chịu tác dụng của tải trọng phân bố theo định lý giới hạn trên và định lý giới hạn dưới. Trên cơ sở phương pháp giải và kết quả tìm được rút ra nhận xét và kết luận.

TỪ KHÓA: Tải trọng giới hạn của tấm, định lý giới hạn trên, định lý giới hạn dưới, phân tích giới hạn.

Abstract: The paper introduces the concept and two general theorems of limit analysis. Then present examples of determined the limited load of plate with edge supported plates subjected to uniform load in the upper bound theorem and lower bound theorem. Comments and draw conclusions based on the method and results.

Keywords: Limited load of plate, upper bound theorem, lower bound theorem, limit analysis.

1. ĐẶT VẤN ĐỀ

Trong tính toán, thiết kế công trình nói chung và tấm nói riêng, xác định tải trọng giới hạn là vấn đề rất cần thiết và quan trọng. Các định lý về phân tích giới hạn là một phương pháp rất hữu ích để người kỹ sư xác định tải trọng giới hạn công trình mà không cần đi sâu vào phân tích dẻo. Vì vậy, trong bài báo, tác giả trình bày về việc xác định tải trọng giới hạn của tấm trên cơ sở các định lý giới hạn nói trên.

2. TRƯỜNG ỨNG SUẤT CHO PHÉP [2],[5],[6]

Xét một vật thể có thể tích V, gọi lực mặt tác dụng trên biên của vật thể là t_i (KG/cm²); lực khối tác dụng bên trong vật thể là b_i (KG/cm³) như Hình 2.1. Ta có các khái niệm sau:

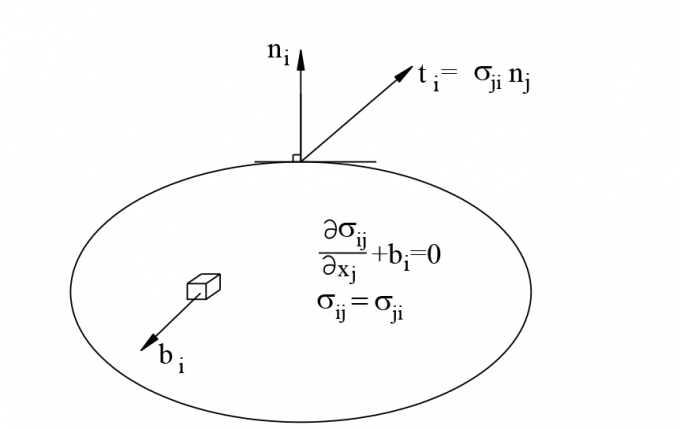Hình 2.1: Mô tả trường ứng suất cân bằng bên trong và trên biên của vật thể

Trường ứng suất cho phép là trường ứng suất thỏa mãn phương trình cân bằng tại mỗi điểm bên trong vật thể và điều kiện ứng suất trên biên vật thể được viết dưới dạng biểu thức như sau:

 

 (1)

 (2)

Với n_j là véc tơ pháp tuyến ngoài tại một điểm trên bề mặt vật thể.

Trường ứng suất tới hạn cho phép là trường ứng suất có sự phân bố của ứng suất thỏa mãn các điều kiện:

- Các phương trình cân bằng lực tại mỗi điểm bên trong vật thể;

- Điều kiện ứng suất trên biên vật thể;

- Thỏa mãn hàm điều kiện dẻo.

Viết dưới dạng biểu thức toán học như sau:

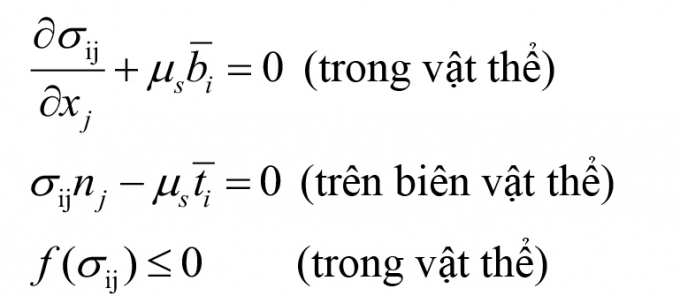(3)

 

(4)

(5)

 

                             

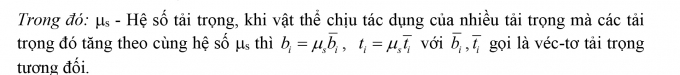3. TRƯỜNG ĐỘNG HỌC CHO PHÉP [2],[5],[6]

Tương tự như trên, ta có mối quan hệ giữa biến dạng và chuyển vị của vật thểđược thể hiện như Hình 3.1.

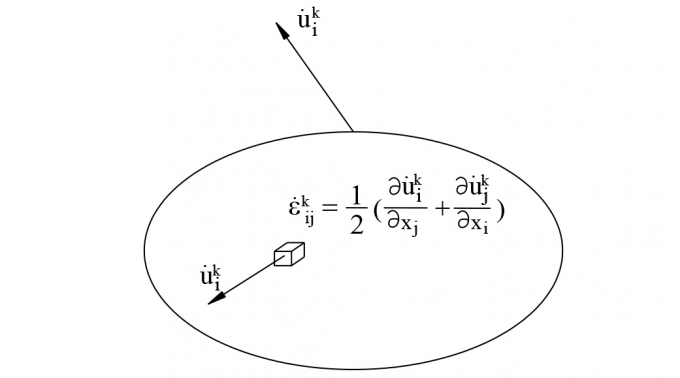Hình 3.1: Mô tả mối quan hệ giữa chuyển vị và biến dạng của vật thể

Trường động học cho phép là trường biến dạng mà thỏa mãn điều kiện liên tục trong vật thể và điều kiện chuyển vị trên biên vật thể (nếu có), viết dưới dạng biểu thức như sau:

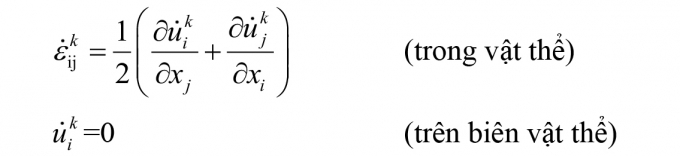 (6)

(7)

 

Trường động học tới hạn cho phép là trường biến dạng có sự phân bố của chuyển vị và biến dạng thỏa mãn các điều kiện sau:

- Phải đảm bảo điều kiện tương thích giữa chuyển vị và biến dạng (phương trình liên tục) bên trong vật thể;

- Các điều kiện về chuyển vị và biến dạng trên biên vật thể;

- Ở vị trí bất kỳ nào trong vật thể có biến dạng thì tại điểm đó trạng thái ứng suất phải thỏa mãn hàm điều kiện dẻo.

Viết dưới dạng biểu thức toán học:

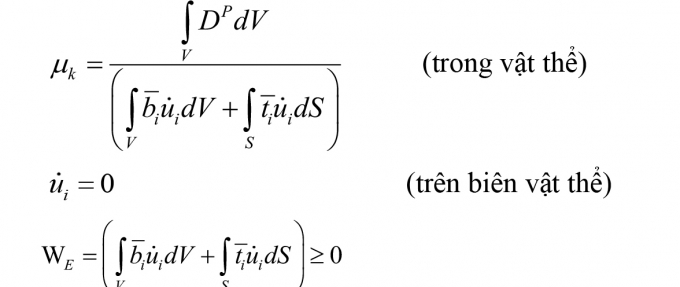 (8)

 

(9)

 (10)

Trong đó: m_k - Hệ số cho phép về động học, D^P - Hàm năng lượng dẻo khuyếch tán, W_E - Công của ngoại lực.

4. ĐỊNH LÝ GIỚI HẠN DƯỚI [2],[5],[6]

Nội dung: Trong tất cả các trường trường ứng suất cho phép, trường ứng suất thực là trường ứng suất xảy ra tương ứng với tải trọng tác dụng lớn nhất.

Viết dưới dạng biểu thức toán học:

`mu` _s^thuc= max (`mu` _s) với `mu` _s thỏa mãn các ràng buộc (3), (4), (5).

5. ĐỊNH LÝ GIỚI HẠN TRÊN [2],[4],[5]

Nội dung: Trong tất cả các trường động học (trạng thái chuyển vị biến dạng) cho phép, trạng thái chuyển vị biến dạng thực là trạng thái xảy ra tương ứng với tải trọng tác dụng nhỏ nhất.

Viết dưới dạng biểu thức toán học:

`mu` _k^thuc= min (`mu` _k) với `mu` _k thỏa mãn các ràng buộc (8), (9), (10).

6. MỘT SỐ VÍ DỤ XÁC ĐỊNH TẢI TRỌNG GIỚI HẠN CỦA TẤM TỰA KHỚP THEO CÁC ĐỊNH LÝ GIỚI HẠN [3]

Xác định tải trọng tới hạn theo định lý giới hạn trên: Cho ta các cơ chế phá hỏng trước, sau đó xác định năng lượng biến dạng dẻo của các cơ chế và biết được năng lượng biến dạng dẻo của cơ chế phá hỏng lớn nhất. Lý thuyết đường trượt cho phép ta xây dựng được các cơ chế phá hỏng có thể xảy ra của kết cấu, trên cơ sở đó xác định được lực tới hạn của các cơ chế phá hỏng và chọn lực tới hạn nhỏ nhất.

Xác định tải trọng theo định lý giới hạn dưới: Theo định lý giới hạn dưới, dựa trên các phương trình cân bằng và điều kiện dẻo xác định được lực phá hỏng tới hạn.

Dưới đây, tác giả khảo sát một vài lời giải của bài toán xác định tải trọng tới hạn (q_th) của tấm vuông cạnh a chịu tác dụng của tải trọng phân bố q theo định lý giới hạn trên và theo định lý giới hạn dưới:

6.1. Xác định tải trọng tới hạn của tấm theo định lý giới hạn trên [3]

Cơ chế phá hỏng của tấm ứng với sự biến đổi nó thành hệ biến hình khi đạt đến khả năng chịu lực có thể biểu diễn theo dạng hình chóp với đỉnh tại điểm O và các cạnh là các khớp chảy dẻo hình trụ, đi từ đỉnh đến chu vi gối. Gọi chiều cao của hình chóp chính là độ võng tại vị trí giữa tấm là w₀ như Hình 6.1:

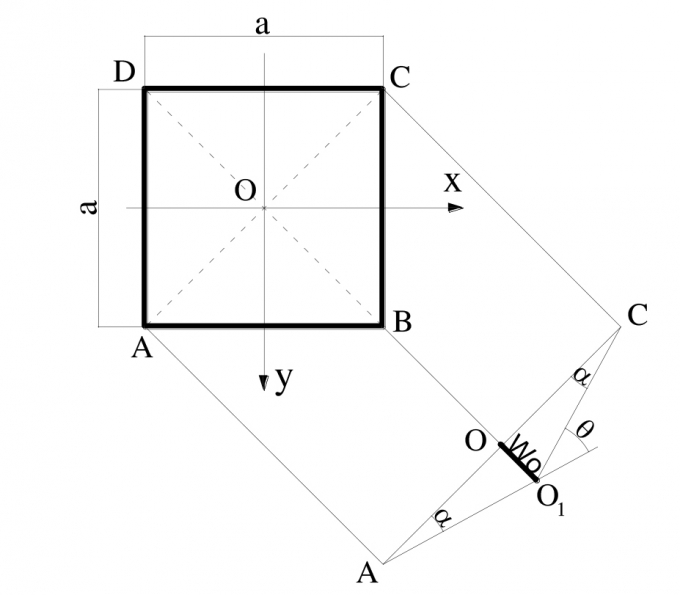Hình 6.1: Cơ chế phá hỏng của tấm

 

    

 

 

 

 

 

 

 

                                      

6.2. Xác định khả năng chịu lực của tấm theo định lý giới hạn dưới [3]

Để xác định tải trọng tới hạn của tấm theo định lý giới hạn dưới cần phải biết phân bố nội lực mô-men trong tấm. Đây là bài toán rất khó vì vậy, người ta chỉ có thể sử dụng định lý giới hạn dưới trong một số trường hợp đơn giản sau:

6.2.1. Tấm vuông cạnh a, liên kết khớp ở chu vi, chịu tác dụng của tải trọng phân bố đều q như Hình 6.2:

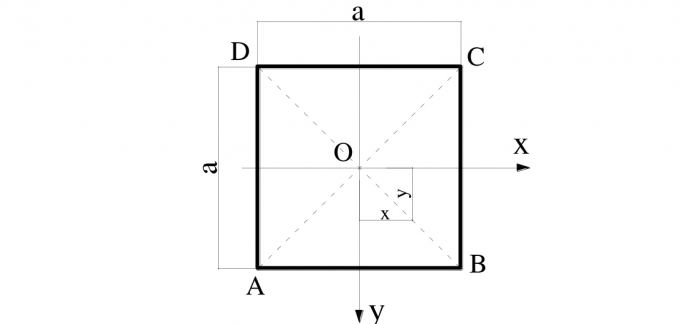Hình 6.2: Tấm vuông cạnh a, liên kết khớp ở chu vi

Vấn đề khó khăn ở đây là tìm được trường ứng suất thỏa mãn các phương trình cân bằng của tấm. Một cách tiếp cận đơn giản là có thể xem tải trọng q được chia thành hai phần bằng nhau, một phần tác dụng lên dầm theo phương trục x, phần còn lại tác dụng lên dầm theo phương trục y. Với một dầm ảo chịu tác dụng của tải trọng là q/2 thì mô-men nội lực thay đổi trong tấm theo quy luật:

Mô-men uốn theo phương của trục x :

 

 

 

 

 

 

 

 

 

Với điều kiện (20) thì:

 

      

                                                                      

 

 

 Nhận xét:

Thông thường, người ta xác định tải trọng giới hạn theo định lý giới hạn trên, dựa vào lý thuyết đường trượt vì nếu sử dụng định lý giới hạn dưới rất khó tìm được phương trình cân bằng và phải đưa ra các lời giải gần đúng nên kết quả nhỏ thua nhiều so với giải theo định lý giới hạn trên.

Khi xác đinh tải trọng giới hạn của tấm theo định lý phân tích giới hạn trên và định lý phân tích giới hạn dưới có ưu điểm là không cần phải phân tích giới hạn dẻo mà xác định được ngay tải trọng giới hạn.

Điều kiện để sử dụng hai định lý phân tích giới hạn là tải trọng phải tăng dần từ 0 theo một tỷ lệ nhất định, nếu không đảm bảo điều kiện này phải sử dụng định lý thích ứng. Trong trường hợp có nhiều lực độc lập tác dụng thì các lực vẫn phải đảm bảo điều kiện tăng theo cùng một hệ số tải trọng.

7. BÀI TOÁN VÀ LỜI GIẢI SỐ

7.1. Bài toán

Tác giả xây dựng bài toán xác định tải trọng giới hạn của tấm vuông tựa khớp chịu tác dụng của tải trọng phân bố theo định lý giới hạn dưới. Để xác định tải trọng giới hạn của tấm theo định lý giới hạn dưới cần phải biết phân bố nội lực mô-men trong tấm, do đó tác giả đã xây dựng bài toán phân tích đàn hồi tấm như sau [4]:

 

 

 

 

 

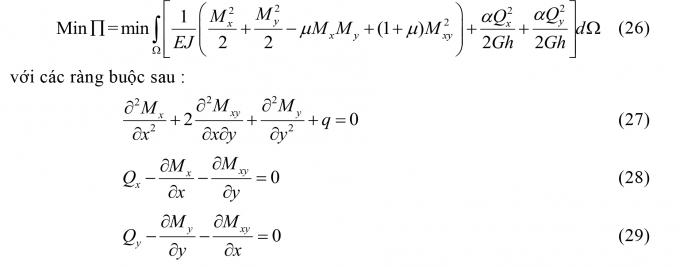Trong đó:

h - Chiều dày tấm;

G - Mô-đun đàn hồi trượt của vật liệu;

a - Hệ số xét đến sự phân bố không đều của ứng suất cắt trên tiết diện khi xét ảnh hưởng của biến dạng trượt ngang. Với dầm có tiết diện chữ nhật đặc, ta có a = 1,2, đối với dầm có tiết diện tròn, a = 1.1... Trong bài báo này, nghiên cứu tấm có tiết diện chữ nhật đặc nên sẽ lấy a = 1,2.

Trên cơ sở đó, bài toán xác định tải trọng giới hạn của tấm có xét biến dạng trượt ngang theo định lý giới hạn dưới được tác giả xây dựng như sau:

q_th = q_max với q thỏa mãn các điều kiện:

- Các phương trình cân bằng: (26), (27), (28), (29);

- Điều kiện biên của nội lực (trên biên của tấm);

- Điều kiện bền Von Mises:

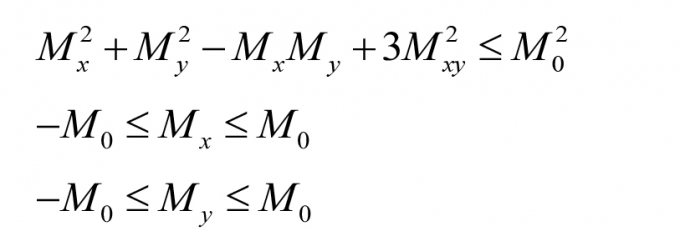 (30)

(31)

(32)

7.2. Lời giải số và phân tích kết quả

Do phương trình cân bằng dùng ẩn là nội lực nên ở đây tác giả sử dụng phương pháp rời rạc hóa bằng sai phân hữu hạn. Trường hợp cần xác định chuyển vị (độ võng w) của tấm ta sử dụng các hàm nội suy đã có của phương pháp phần tử hữu hạn để giải.

Để giải bài toán này tác giả viết chương trình trong môi trường Matlab, chia tấm thành nxn phần tử. khi viết chương trình giải các bài toán, tác giả sử dụng các đại lượng không thứ nguyên như sau:

Tải trọng tác dụng: p = 1 đơn vị;

Chiều dài cạnh của tấm (tấm vuông): l_x = l_y = a = 1;

Độ cứng trụ của tấm: D = 1;

Mô-men dẻo M₀  = 1.

Vì vậy, với tấm chịu tác dụng của tải trọng phân bố đều q thì:

 

 

 

Theo kết quả của bài toán đàn hồi [4] thì khi chia tấm thành càng ít số phần tử, thì mô-men nội lực max (tại tâm tấm) càng nhỏ, tức là càng nhỏ thua giá trị mô-men giới hạn nên tấm chịu lực càng tốt hay lực tới hạn P_th càng lớn.

Ngược lại, khi ta chia tấm thành số phần tử càng lớn (kết quả bài toán càng chính xác) thì mô-men nội lực tại tâm tấm càng lớn (càng gần giá trị mô-men giới hạn) nên khả năng chịu lực của tấm càng nhỏ hay lực tới hạn P_th càng nhỏ.

 Khi cứ tăng dần số phần tử, lực tới hạn càng nhỏ, đến một lúc nào đó tấm sẽ làm việc đàn hồi. Vì vậy, để xác định lực tới hạn tác giả sẽ tăng dần số phần tử đến khi trong tấm còn ít nhất hai điểm chảy dẻo (một điểm tại tâm tấm và một tại góc tấm) đủ để có khuynh hướng tạo thành đường khớp dẻo và sẽ lấy giá trị lực tới hạn ứng với trường hợp đó làm lực tới hạn P_th của bài toán.

Sau đây tác giả trình bày kết quả bài toán khi chia tấm thành số các phần tử tăng dần:

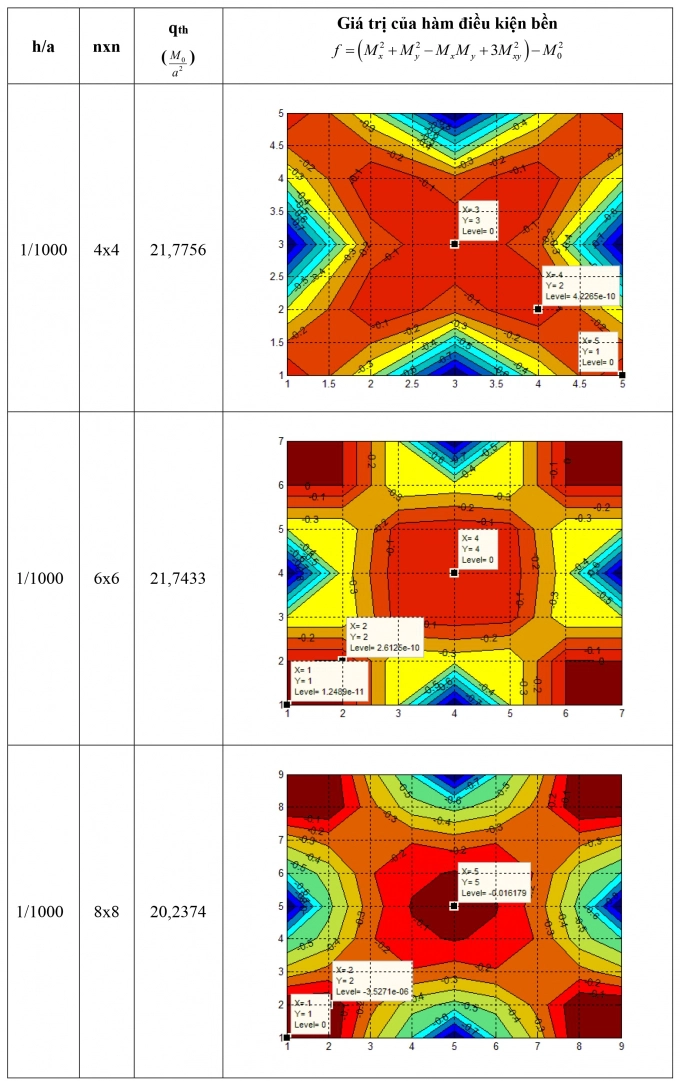Hình 7.1: Kết quả phân tích giới hạn tấm vuông tựa khớp chịu tác dụng tải trọng phân bố

Nhận xét: Theo kết quả trên Hình 7.1 thì:

- Khi tăng dần số phần tử thì số phần tử càng nhiều lực tới hạn càng nhỏ.

- Trong các trường hợp n = 4, 6 kết quả trên Hình 7.1 cho thấy tại vị trí đỉnh và bốn góc tấm đều có f = 0 hoặc f » 0 tức là các vị trí này chảy dẻo, các đường khớp dẻo hình thành theo xu hướng đi từ đỉnh tấm đến 4 góc tấm.

- Nếu tiếp tục tăng dần số phần tử tấm đến n = 8, tại đỉnh tấm có f = - 0,016179 < 0, như vậy đỉnh tấm vẫn làm việc ở trạng thái đàn hồi. Lúc này tấm chưa thể hình thành các đường khớp dẻo và do đó chưa thể hình thành cơ chế phá hỏng, tấm vẫn làm việc đàn hồi.

Vậy tải trọng tới hạn ta sẽ lấy ứng với trường hợp ngay sau khi tấm chuyển từ trạng thái làm việc đàn hồi sang dẻo, tức ứng với n = 6, khi đó lực tới hạn là:

 

 

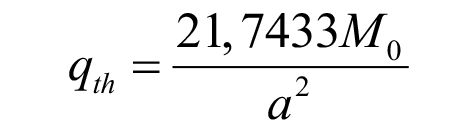Chú ý: Trên cơ sở thuật toán này, tác giả đã viết và giải bài toán xác định tải trọng giới hạn của tấm tựa khớp, tấm trên nền đàn hồi chịu tác dụng của tải trọng tập trung và đều cho kết quả đúng đắn.

Tài liệu tham khảo

[1]. N.I.Bêdukhốp (1978), Cơ sở lý thuyết đàn hồi, lý thuyết dẻo, lý thuyết từ biến, Người dịch: Phan Ngọc Châu, NXB. Đại học và Trung học chuyên nghiệp, Hà Nội.

[2]. Jan A.Konig (1987), Shakedown of  Elastic - Plastic structures, Elsevier Science Publishing Co, Inc.

[3]. Milan Jirasek, Zdenek P. Bazant, Inelastic Analysis of Structures, John Wiley & Sons, LTD.

[4]. ThS. Mai Thị Hải Vân, TS. Đỗ Ngọc Viện (2015), Phương pháp tính tấm chữ nhật chịu uốn có xét biến dạng trượt ngang sử dụng nội lực làm ẩn, Tạp chí GTVT, số 7.

[5]. Vu Duc Khoi, Dual Limit and Shakedown Analysis of Structures, Doctoral Thesis (2001), University of Liege faculty of Applied sciences.

[6]. Wai-Fah Chen (2008), Limit Analysic and soil Plasticity, J.Ross Publishing.