Thuật toán điều khiển tàu biển hành trình theo tàu dẫn đầu

TS. Nguyễn Xuân Phương Trường Đại học Giao thông vận tải TP. Hồ Chí Minh Người phản biện: PGS. TS. Vũ Ngọc Bích PGS. TS. Lê Hữu Sơn

Tóm tắt: Bài báo trình bày nghiên cứu xây dựng thuật toán điều khiển tàu biển hành trình theo tàu dẫn đầu. Trong thực tiễn hàng hải, khi tàu biển hành trình qua kênh, luồng hẹp, theo yêu cầu của cơ quan điều hành, người ta sẽ yêu cầu hành trình theo đoàn, dưới sự chỉ huy của tàu dẫn đầu. Bài toán áp dụng để điều khiển tàu hành trình theo đoàn, cụ thể là xác định được luật điều khiển theo tần số chuyển động quay của máy chính; quãng đường tàu cần đi qua để lọt vào vùng điều khiển.

Từ khóa: Điều khiển tàu theo hành trình dẫn đầu, bài toán thành lập các đoàn tàu theo đội hình, luật điều khiển theo tần số chuyển động quay của máy chính.

Abstract: This paper presents the research for Algorithms of Ship Control in Navigation Following of the Leading Vessel. In Nautical practice, as the vessel passing through the channel, it must sail in convoy that follows the leading ship. The problem is applied for ship control in convoy, such as finding of the control referred to rotation frequency of Main Engine; the sailed distance for entry the control area.

Keywords: Ship control following the leading ship, the problem for ship in convoy, the control referred to rotation of main engine.

1. Mở đầu

Khi đi qua các kênh dẫn tàu, các nhịp cầu quay, cụ thể như khi đi qua các đoạn sông cửa đập sẽ phát sinh bài toán thành lập các đoàn tàu theo đội hình, nghĩa là bài toán về các chuyển động ngược chiều gặp nhau. Việc thành lập đội hình được bắt đầu từ tàu chỉ huy đi đầu (đoàn tàu). Nhiệm vụ các tàu còn lại (hay các hệ thống di động) là nhanh chóng vào vị trí của mình và thống nhất các tham số chuyển động với các tàu đi trước. Trong hoàn cảnh đó cần phải hoàn thành việc đánh giá động lực học của các hệ thống di động, các giá trị ban đầu về tọa độ pha từ góc độ làm thế nào để bản thân con tàu có thể tiếp cận nhanh hơn tới tàu chỉ huy [1, 2, 3].

Để đạt được mục tiêu này, tác giả đề xuất xét các cách giải dựa trên phương pháp tiếp cận Maierovsky trong nguyên lí cực tiểu, cho phép ta đưa các giải pháp phân tích đáng quan tâm đến những giá trị số.

2. Thuật toán điều khiển

Vận dụng hệ phương trình [1, 3]:

 

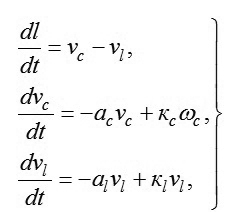(1)

 

 

 

 

Trong đó:

l - Khoảng cách giữa tàu dẫn đầu và tàu đi theo;

ν_c- Vận tốc của tàu đi theo;

ν_l- Vận tốc của tàu dẫn đầu;

 ω_l- Tác động điều khiển của tàu dẫn đầu (tần số quay của máy chính);

ω_c- Tác động điều khiển của tàu đi theo (tần số quay của máy chính);

- Các hệ số hằng số.

Các giới hạn áp đặt lên các tác động điều khiển là:

 

                     (2)

Đại lượng ω_l được xác định bởi một hệ con cố định xuất phát từ công nghệ hành trình cho trước của đoàn tàu. Trình điều khiển ω_c do người lái con tàu trong đoàn lựa chọn [5]. Trình điều khiển đó cần phải sao để trên đoạn thời gian t = 0 ÷ t_k, những điều kiện sau phải được thực hiện:

 

 

Ở đây, t_k- Thời điểm kết thúc chuyển động có điều khiển của tàu.

Coi ω_l và ν_l là những đại lượng không đổi, nghĩa là chuyển động của tàu dẫn đầu luôn ổn định.

Ta hãy tìm quy luật điều khiển theo tần số chuyển động quay của máy chính tàu, để đảm bảo trong khoảng thời gian cực tiểu có thể đạt được sự ngang nhau của các vận tốc ν_l  = ν_c và khoảng cách giữa tàu “dẫn đầu” và tàu đi theo sẽ đạt        [1, 4, 5, 6].

Đưa thêm vào đây một tọa độ mới:

T= x    (3)

trong đó: T << t_k .

Chỉ tiêu điều khiển có tính đến (3) có dạng:

 

 

Hàm Hamilton:      

 

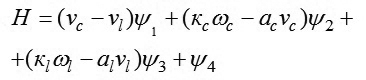              (4)

 

Phương trình để xác định các tham biến phụ trợ [5]:

 

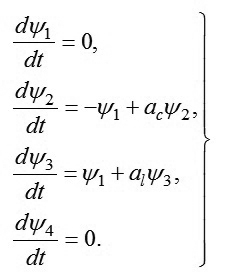(5)

 

 

 

 

 

Ta viết các điều kiện tác động ngang transversality:              

 

 

 

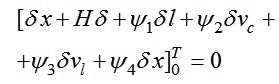Bài toán này có tích phân bậc 1. Do T - Đầu phải tự do và khi t = 0 thì t = 0, ν = const , ν_c = 0, l = 0; còn khi t = T, ν_l = ν_c, l = l_k  đẳng thức (4) có thể, khi:

 

         (6)

Nhưng H = const trên đoạn t = 0 ÷ T [7], cho nên tích phân bậc nhất của bài toán sẽ là:   

 

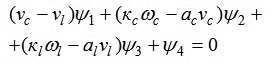        (7)

 

Hàm chuyển mạch tác động điều khiển được xác định từ biểu thức dạng sau [8]:

 

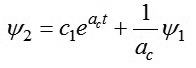                          (8)

 

Từ hệ (5) suy ra: ψ₁ = const  trên đoạn t = 0 ÷ T .

Ta cần tìm các hằng lượng c₁và ψ₁ trong phương trình (8). Để làm như vậy, ta viết tích phân bậc nhất đối với thời điểm t = t_ϊcó tính đến (6), trong đó, t_ϊ là thời điểm, khi hàm thay ψ₂ đổi dấu, nghĩa là khi diễn ra sự chuyển mạch các tác động điều khiển ω_c:

                  ψ₁ (ν_c = ν_l) - 1 = 0

Từ đó ta có:    

 

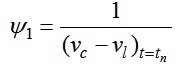     (9)

 

Tại thời điểm t = t_ϊ ,ν_c = ν_cmax.

Ta lại viết tích phân bậc nhất đối với thời điểm t = 0:

 

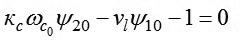  (10)

Từ phương trình (10) ta tìm ra giá trị ban đầu của đại lượng ψ₂₀:

 

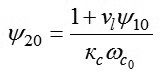    (11)

 

Và từ các đẳng thức (8), (9), (10) ta xác định được hằng lượng c₁

 

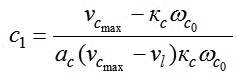 (12)

 

Bây giờ ta sử dụng tích phân bậc nhất và công thức (8) để tìm thời gian điều khiển t = T và thời điểm chuyển mạch tác động điều khiển t = t_ϊ. Tại thời điểm t = T ta có [7, 8]:

       

 

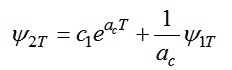(13)

 

Áp dụng biểu thức (7) đối với t = T, ta được:

 

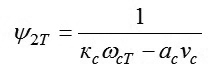(14)

 

Thay các phương trình (9), (12) và (14) vào (13) rồi giải biểu thức thu được đối với tham biến chưa biết T, ta có:

 

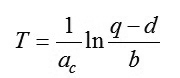(15)

 

Trong công thức (15) đã đưa vào các kí hiệu sau:

 

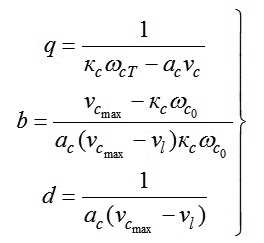(16)

 

 

 

 

 

Cần xác định thời điểm chuyển mạch tác động điều khiển ω_c. Để làm được như vậy, ta viết lại các phương trình (8) với thời điểm t = t_n

 

 

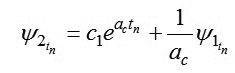Nhưng vì khi t = t_ϊ, ψ₁ = 0 , cho nên:

 

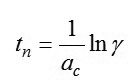(17)

 

Trong đó:

 

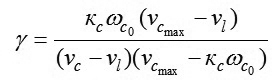(18)

 

Ta phải tìm quãng đường mà tàu cần phải đi qua để lọt vào vùng điều khiển. Từ hệ phương trình (1) ta thu được:

 

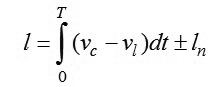             (19)

 

Ở đây, l_n - Khoảng cách ban đầu giữa tàu “dẫn đầu” và tàu đi theo [6].

Xét ví dụ sau, áp dụng những biểu thức đã thu được, tìm giá trị số của các đại lượng T, t_n và l. Cho trước các hệ số sau:

 

 

 

Các giá trị ban đầu của tọa độ pha khi tính đến các giới hạn (2) là:

 

 

 

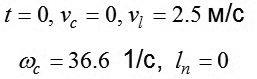Còn các giá trị cuối của tọa độ sẽ là:

 

 

 

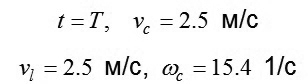Trị số lớn nhất của vận tốc chuyển động dọc của tàu là:

 

 

Giá trị các thành phần hợp thành của vec-tơ ψcó tính đến (11) tại thời điểm t = 0 là: ψ₁₀ = 0,2924, ψ₁₀ = 16,66.

Vận tốc chuyển động của tàu “dẫn đầu” được coi là không đổi trên đoạn t = 0 ÷ T và bằng ν_l = 2,5 M/C .

Làm các phép tính theo các công thức (15), (16), (17), (18) và (19), ta sẽ thu được những giá trị của các tham biến cần biết như sau:

 

 

 

 

 

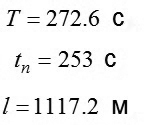3. Kết luận

Điều kiện tối ưu của trình điều khiển đặc biệt đối với các chế độ vận hành Hệ động lực, do có liên quan đến những phép biến đổi giải tích phức tạp, nên cần được kiểm tra bằng phương pháp số.

Các phương pháp được thiết lập trong bài báo này giúp tìm ra các trình điều khiển mà không cần sử dụng trực tiếp các phương pháp Eton và Neistad.

Đồng thời, kết quả nghiên cứu đã đề xuất ra các phương pháp thiết lập thuật toán điều khiển theo nguyên lí cực tiểu mà cơ sở của chúng là sự lựa chọn các điều kiện tác động ngang, nhờ đó cho phép ta không những thu được các giải pháp chất lượng, mà còn thu được những giải pháp định lượng. Cụ thể hơn là xây dựng được các thuật toán điều khiển Hệ động lực, cho phép thực hiện tiếp cận an toàn với tàu dẫn đầu.

Tài liệu tham khảo

[1]. Кулибанов Ю. М. (1990), Оптимизация эксплуатационных режимов работы дизельных энергетических установок судов внутреннего плавания, Диссертация на соискание ученой степени доктора технических наук. -Л.

[2]. Кулибанов Ю. М. (1998), Основы системотехники, Учебное пособие, – Л.: ЛИВТ, 46 с.

[3]. Кулибанов Ю. М. (1996),Судно как объект многосвязного регулирования при оптимальном управлении главными двигателями, Тр. ин-та: Экономика и организация перевозок, ЛИВ, часть I. - с. 78 - 88.

[4]. Кулибанов Ю. М., Кулибанов М. Ю. (1999), Групповое поведение в системах человек-машина, Сб. научных трудов «190 лет транспортного образования» СПб.: СПГУВК, с.184-188.

[5]. Kose, K. (1982),On a New Mathematical Model of Maneuvering  of A Ship and Its   Applications, International Shipbuilding Progress, 336. pp. 201-219.

[6]. Кулибанов Ю. М., Кулибанов М. Ю. (1998), Особые управления в человеко-машинных системах оптимизации расхода топлива, Сб. научных трудов «Методы прикладной математики в транспортных системах»  выпуск II, СПб.: СПГУВК, с. 78-83.

[7]. Ольшамовский С. Б., Земляновский Д. К., Щепетов И. А. (1972), Организация безопасности плавания судов, - М.: Транспорт, - 215 с.

[8]. Маслов Ю.В. (2004), Энергосберегающие технологии в управлении движением судов на внутренних водных путях, СПб.: Судостроение, г., 245 с.