Xác định lực căng trong cáp cầu dây văng bằng phương pháp đồ thị

ThS. NCS. Nguyễn Trọng Nghĩa Trường Đại học Giao thông vận tải TS. Hoàng Nam Trường Đại học Bách khoa TP. Hồ Chí Minh PGS. TS. Nguyễn Ngọc Long Trường Đại học Giao thông vận tải Người phản biện: TS. Phạm Hoàng Kiên GS. TSKH. Nguyễn Văn Khang

Tóm tắt: Xác định lực căng của cáp trong cầu dây văng hay cáp dự ứng lực (DƯL) ngoài trong giai đoạn khai thác là rất cần thiết cho việc kiểm tra và đánh giá thường xuyên cầu treo dây văng. Phương pháp phổ biến nhất hiện nay để xác định lực căng trong cáp bằng thực nghiệm là phương pháp dựa trên kết quả đo dao động xác định tần số dao động riêng thứ nhất của cáp. Tuy nhiên, phương pháp này có thể không chính xác trong trường hợp các thông số độ võng và độ cứng chống uốn của cáp lớn. Trong nghiên cứu này, dựa trên các phương trình đặc trưng dao động riêng cáp có xét đến độ võng và độ cứng chống uốn với nhiều dạng dao động khác nhau. Bằng cách xem xét các giả định đơn giản hóa các thông số độ cứng để tìm ra lời giải của phương trình thu được và xác định lực căng của cáp dựa trên các dạng dao động khác nhau. Phương pháp này sử dụng kết quả đo dao động để tính toán lực căng trong cáp dựa trên tần số dao động theo các dạng dao động khác nhau của cáp. Kết quả nghiên cứu được áp dụng đánh giá lực căng trong cáp của cầu Phú Mỹ dựa trên số liệu  đo dao động thực tế của 4 cáp cầu dây văng Phú Mỹ, TP. Hồ Chí Minh.

Từ khóa: Cáp, lực căng, võng, uốn, độ rung, tần số tự nhiên.

Abstract: Estimating cable tension in cable-stayed bridges or in external tendons is essential for regular inspection and  assessment  of  those  structures. Vibration  measurements  provide  a  solution,  however,  may  not  be accurate in cases parameters such as amount of sag and flexural rigidity of cable are significant.  In this study, the characteristic equation for vibration of the most general case of a cable, where both the sag and flexure  in  the  cable  are  taken  into  account,  is  analytically  derived. After  that  by 

Keywords: Cable, tendons, Vibration, parameters

1. Giới thiệu chung

Việc xác định lực căng trong cáp là một vấn đề quan trọng để kiểm soát trạng thái làm việc theo thời gian của các cáp dây văng trong cầu dây văng và cầu khẩu độ lớn sử dụng cáp DƯL ngoài. Trong các nghiên cứu trước đó, cách tiếp cận bán thực nghiệm hoặc mô hình số học đã được sử dụng để đánh giá lực căng trong cáp dựa trên một mô hình đơn giản lý tưởng hóa. Kovacs (1982) lần đầu tiên xác định đươc sự hiện hữu của một kích thước tối ưu cho cáp DƯL ngang được thêm vào bộ giảm chấn dạng nhớt. Sau đó, Yoneda - Maeda (1989), Uno và cộng sự (1991) đã tiến hành nghiên cứu số học về kích thước bộ giảm chấn tối ưu và đã chỉ ra rằng khả năng giảm chấn tối đa có thể đạt được tỷ lệ thuận với khoảng cách giữa bộ giảm chấn và neo cáp và độc lập với số mode dao động. Đáng chú ý là kết quả nghiên cứu của Pacheco và các cộng sự (1993) về hướng đơn giản hóa các bước thiết kế giảm chấn dạng nhớt cho cáp văng. Gần đây, hiệu ứng uốn ở các phương thức giảm chấn của cáp căng với bộ giảm chấn đã được nghiên cứu phân tích bởi nhiều tác giả trong đó có kết quả nghiên cứu của (Hoang và Fujino 2007).

Tại Việt Nam, ngày càng nhiều các dự án cơ sở hạ tầng mới ở cấp quốc gia được lên kế hoạch và ngày càng có nhiều cầu được xây dựng. Cho đến nay, đã có nhiều công trình cầu treo được xây dựng và đưa vào khai thác có chiều dài nhịp chính trên 300m như: Cầu treo dây võng Thuận Phước (nhịp chính 450m), cầu dây văng Mỹ Thuận (nhịp chính 350m); Cần Thơ (nhịp chính 550m); Rạch Miễu (nhịp chính 270m); Bãi Cháy (nhịp chính 435m) và gần đây nhất là cầu Phú Mỹ tại TP.Hồ Chí Minh (nhịp chính 380m, Hình 2.3a, 2.3b), cầu Nhật Tân (nhịp chính 300m).

Ngoại trừ cầu Mỹ Thuận là cầu treo dây văng có nhịp lớn đầu tiên tại Việt Nam thì các cầu treo dây văng khác đều được lắp đặt hệ thống quan trắc sức khỏe (hệ thống SHM) như cầu Rạch Miễu, cầu Cần Thơ, cầu Nhật Tân... Tuy nhiên, ngay cả với các cầu đã lắp đặt hệ thống quan trắc thì chỉ một số nhỏ các cáp được lắp đặt sensor đo kiểm tra lực căng bằng Loadcell hoặc đầu đo gia tốc. Do vậy, vẫn cần các giải pháp thực nghiệm hoặc bán thực nghiệm để xác định và kiểm soát lực căng của cáp trong giai đoạn vận hành, khai thác cầu. Trong nghiên cứu này, nhóm nghiên cứu đề xuất phương pháp đánh giá lực căng của cáp bằng phương pháp bằng đồ thị, nhằm đánh giá một cách rõ ràng lực căng trong cáp so với các phương pháp sử dụng trước đây và có xét đến các thông số như độ võng, độ cứng chống uốn của cáp, cũng như ảnh hưởng của bộ giảm chấn trong cáp.

2. Cơ sở lý thuyết

2.1. Phương trình dao động cơ bản của cáp

Phân tích mô hình dao động của một cáp nghiêng dưới tác dụng của lực căng T như thể hiện trong Hình 2.1. Hệ tọa độ khảo sát theo trục x dọc theo trục cáp và trục y theo hướng vuông góc. Thông số tính toán của cáp: Khối lượng trên đơn vị chiều dài: m, chiều dài dây cáp L, độ cứng chống uốn EI và góc nghiêng θ so với phương nằm ngang (0 ≤ θ < π/2). Phương trình dao động của cáp trong mặt phẳng v(x, t) (theo phương y) được Fujino và Hoàng 2008^[1], Hiroshi Zui và cộng sự 1996^[2] đề xuất như sau:                                                  

 

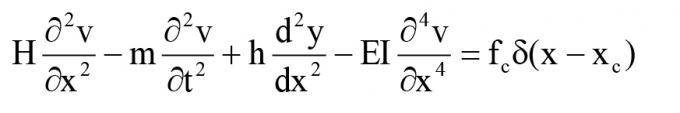(1)

 

Trong đó: H = Th/cosθ - Lực căng dây; T_h - Thành phần lực theo phương ngang của lực căng cáp; δ(x-x_c} - Hàm Dirac xác định hiệu quả của lực giảm chấn f_c(t) ở vị trí x = x_c; v(x, t) - Dao động theo phương ngang (hướng trục y).

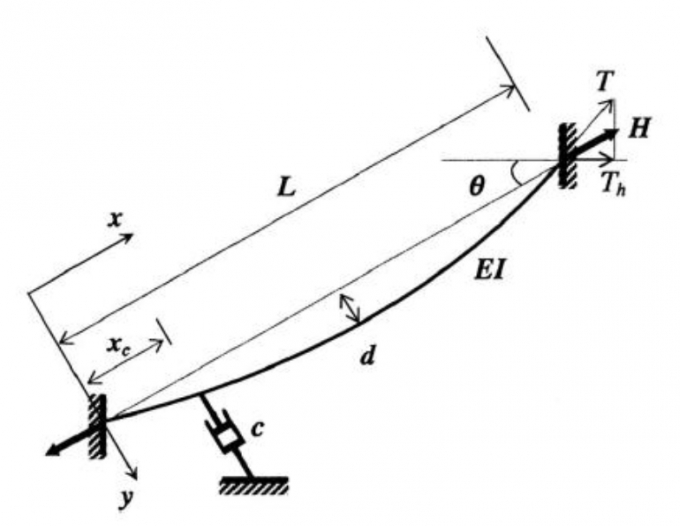Hình 2.1: Mô hình phân tích dao động của 1 cáp nghiêng

 

Công thức (1) đã giả thiết rằng lực căng T là đủ lớn để độ võng của cáp có thể được biểu diễn chính xác bằng đường parabola (Irvine 1981)^[3].

 

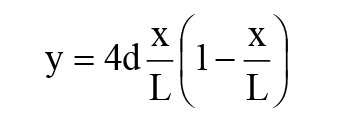(2)

 

Với d - Độ võng tại vị trí giữa của cáp, d = mgL²cosθ/(8H), g - Gia tốc trọng trường. Trong công thức (1), h(t) là lực căng biến đổi theo vị trí, lấy được từ khả năng tương thích giữa tính đàn hồi và hình học của phần tử cáp (Irvine và Caughey 1974)^[4].

 

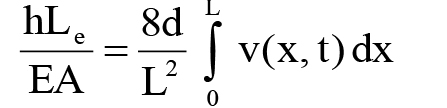(3)

 

Trong đó: EA - Độ cứng dọc trục của cáp và .L_e = L[1+8](d/L)² công thức (1) tương ứng với các trường hợp chung nhất của cáp khi xét đến cả độ võng và độ cứng chống uốn đều được đưa vào tính toán. Đối với dao động tự do của cáp, hàm chuyển vị, lực cản của giảm chấn và lực căng biến đổi theo vị trí được viết lại như sau:                     

 

(4)

Trong đó: i² =-1, ω - Tần số dao động riêng,

- Hàm dạng dao động riêng của cáp. Phương trình đã được nghiên cứu bởi tác giả đầu tiên đánh giá hiệu ứng giảm chấn của dây cáp văng với bộ giảm chấn (Fujino và Hoàng 2008). Hai thông số quan trọng là (i) thông số độ võng λ² xác định bởi Irvine và Caughey (1974):

 

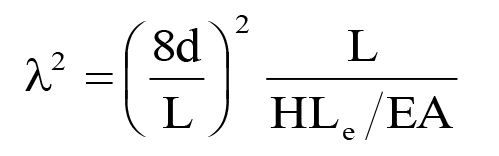(5)

 

 (ii) - Độ cứng chống uốn e (Hoang and Fujino 2007)^[5]:                                                            

 

 (6)

Xem xét sự dao động tự do của dây cáp với tần số tự nhiên ω. Từ đó, biểu thị các tham số thứ nguyên ví dụ số bước sóng               , phương trình đặc trưng sau đây cho bcó thể được suy ra (Fujino và Hoang 2008) khi lực giảm chấn = 0:

        (7)

 

 

 

 

 

 

 

 

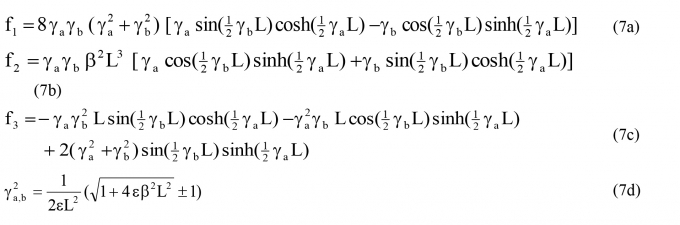Cần lưu ý rằng, trong trường hợp dạng dao động không đối xứng thì độ võng sẽ không làm tăng thêm lực căng cho cáp. Kết quả là tồn tại các nghiệm khác nhau của phương trình (7) cho các dạng dao động gần đối xứng và bất đối xứng của cáp có giảm chấn. Với dạng dao động bất đối xứng (mode dao đông thứ n = 2, 4,…), số bước sóng có thể xác định bằng cách cân bằng giá trị f₁ đầu tiên ở công thức (7) đến giá trị 0:

 

(8)

Với các dạng dao động đối xứng (mode dao động thứ n = 1, 3,…), tính các phần trong dấu ngoặc bằng 0, ta được:

 

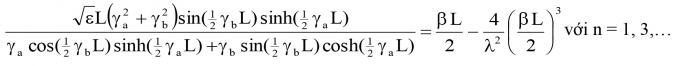(9)

 Phương trình (7) và kết hợp với (8 & 9) là phương trình siêu việt, có thể giải được với số tham số bsử dụng phương pháp số lặp, như Newton-Raphson, bắt đầu bằng một giá trị thích hợp. Ta thấy phương trình này hàm chứa một loạt các vấn đề với một trong hai tham số: Tham số độ võng λ² hoặc tham số độ cứng chống uốn eđược kèm theo riêng biệt. Ví dụ, số bước sóng của một dây cáp uốn căng (λ²= 0) được xác định bằng cách cân bằng kết quả của phép tính f₁× f₂ về 0, mà có kết quả tương tự như phương trình cáp đặc trưng đề xuất bởi Zui và cộng sự (1996). Khi λ² ≠ 0, trong giới hạn của độ cứng chống uốn e  0, sau khi sắp xếp lại biểu thức trong ngoặc và đưa nó về 0, ta thu được phương trình số bước sóng cho cáp võng (không uốn) được thành lập bởi Irvine và Caughey (1974).

2.2. Xác định lực căng trong cáp bằng phương pháp đồ thị

Lực căng dây cáp có thể xác định thông qua mối quan hệ của nó với số bước sóng. Với các phương trình siêu việt - phương trình 8 & 9 với thông số bước sóng β_on của một dạng dao động thứ n, và do đó lực căng của dây cáp có thể không được xác định một cách rõ ràng. Tuy nhiên, bằng cách xem xét một cách đơn giản hóa bằng các giả thiết rằng thông số độ cứng chống uốn nhỏ, lực căng dây cáp có thể tính toán một cách đơn giản.

Với elà nhỏ nên 4εβ_onL²< 1, từ phương trình (7d), các xấp xỉ sau đây có thể được suy ra:

 

 

 

 

 

 

 

 

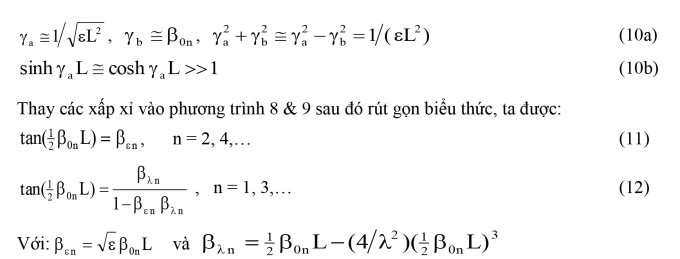Phương trình (11) và (12) là sự mở rộng hợp lý của phương trình bước sóng cho dạng dao động mode chẵn và mode lẻ của cáp có độ võng d, được đưa ra bởi Irvine và Caughey (1974), để xét đến độ cứng chống uốn của cáp. Chú ý rằng, với cầu dây văng nhịp lớn có giá trị λ²  thông thường nhỏ hơn 3 (Tabatabai và Mehrabi 2000^[6]), với ε = 2.5×10^-6 ~ 10^-4 theo đề xuất của Hoang và Fujino, 2007. Các biểu đồ dao động của β_on với 6 dạng dao động (n = 1 ~ 6) ứng với giá trị ε = 10^-4 có thể biểu diễn như Hình 3.3. Trong hình này số bước sóng của cáp võng theo phương trình Irvine and Caughey (ε = 0) được thể hiện bằng đường mảnh để minh hoạ. Nó thể hiện độ cứng chống uốn cáp gây ra một số thay đổi nhỏ trong số bước sóng những mode đầu tiên, nhưng sau đó sự thay đổi sẽ rõ ràng hơn ở những mode cao. Sự thay đổi xảy ra khá ổn định liên quan đến thông số độ võng đối với cả mode dao động chẵn và lẻ. Tính chính xác của các phương trình tiệm cận (11) và (12) có thể được chứng minh bằng cách so sánh kết quả của nó với các lời giải chính xác của phương trình (8) và (9) trong Hình 3.2.

Sử dụng các phương trình đơn giản (11) và (12) có thể dễ dàng tính toán số bước sóng hay tần số dao động tự nhiên của cáp khi xét đến độ cứng chống uốn và độ võng, từ đó suy ra lực căng và thuộc tính của cáp. Bằng cách này đường cong liên hệ giữa lực căng cáp và tần số tự nhiên có thể được xây dựng, từ việc ước tính lực căng cáp thông qua tần số tự nhiên đo được. Lực căng theo mode dao động thứ n phụ thuộc vào độ võng của cáp. Với cáp ngắn có độ võng nhỏ, dạng dao động mode đầu tiên là rất quan trọng, trong khi các dạng dao động có mode cao hơn sẽ được dùng để ước tính chính xác hơn cho các cáp dài (Hiroshi Zui và cộng sự 1996).

3. Xác định lực căng trong cáp của cầu Phú Mỹ bằng phương pháp đồ thị

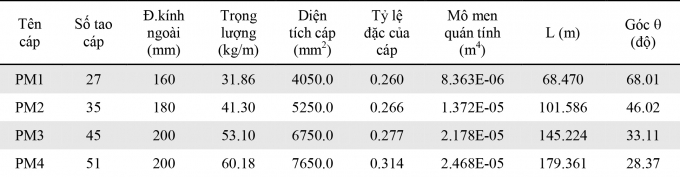
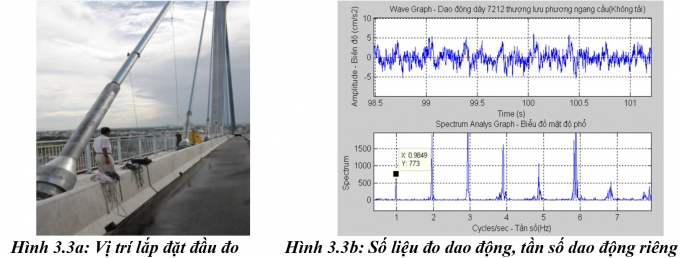
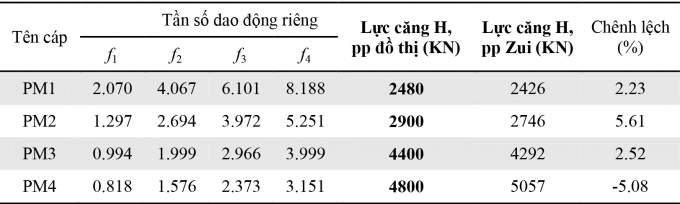
Để kiểm tra phương pháp đề xuất trên trong việc xác định lực căng của cáp dựa trên lý thuyết kế hợp với thực nghiệm, nhóm nghiên cứu sẽ sử dụng số liệu đo đạc thực tế của cầu treo dây văng Phú Mỹ, TP. Hồ chí Minh. Cầu được khởi công từ tháng 9/2005 và thông xe vào ngày 9/9/2009. Thông số kỹ thuật chính của cầu dây văng được thể hiện trong Hình 3.1a, 3.1b^[7]. Thông số kỹ thuật của 4 cáp đo PM1, PM2, PM3, PM4 được thể hiện trong Bảng 3.1. Kết quả đo tần số dao động tư nhiên và lực căng cáp được thực hiện trong điều kiện thời tiết bình thường với nhiệt độ từ 32^oC đến 35^oC, tốc độ gió từ 2,0 đến 11,2m/s (Bảng 3.2).

Hình 3.1a: Cầu Phú Mỹ khi hoàn thành

 

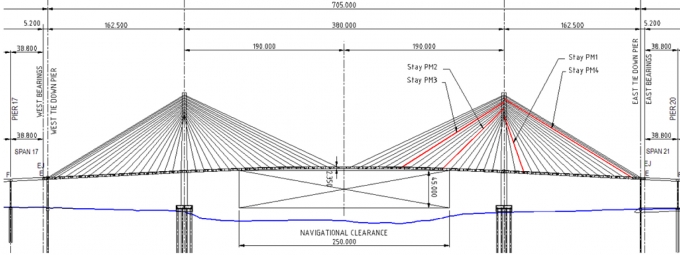Hình 3.1b: Bố trí chung cầu dây văng và các dây xác định lực căng (PM1, PM2, PM3, PM4)

 

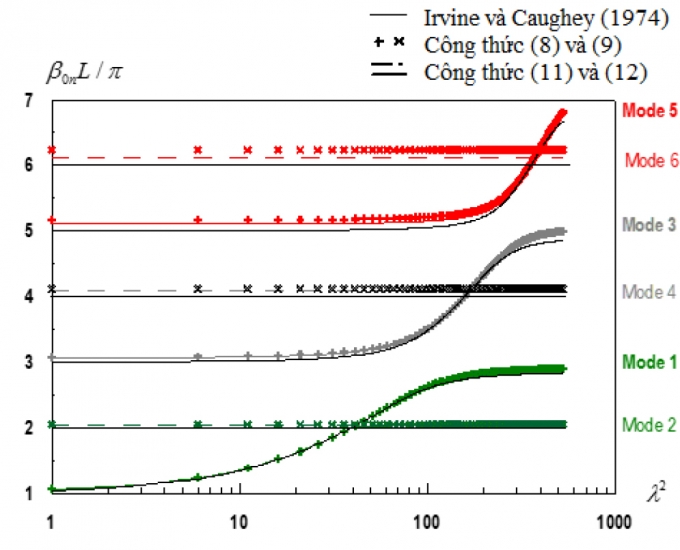Hình 3.2: Mối quan hệ giữa βon và λ2 ứng với 6 dạng dao động đầu tiên (ε = 10-4)

 

Bảng 3.1. Các thông số của cáp PM1, PM2, PM3, PM4

 

 

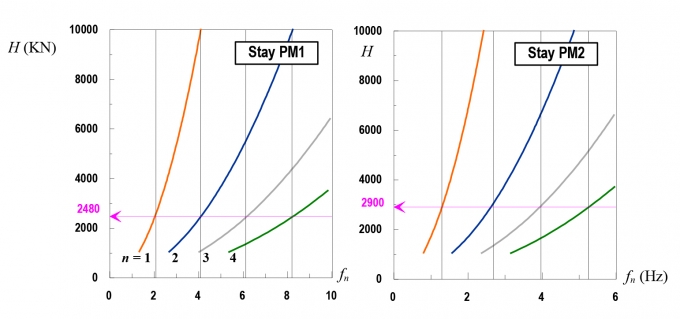
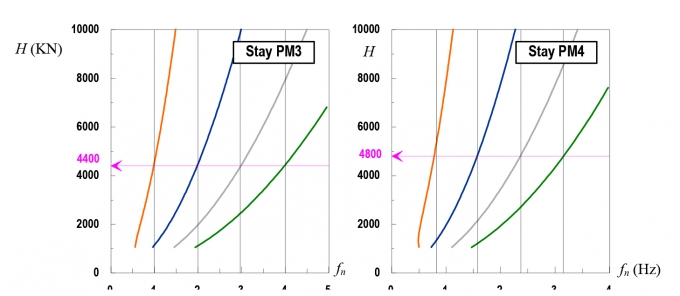
Xây dựng đồ thị lực căng của các cáp PM1, PM2, PM3, PM4 theo 4 dạng dao động đầu tiên (n=1, 2, 3, 4) sau đó dựa vào tần số của 4 dạng dao động đầu tiên đo được lên đồ thị lực căng và xác định được lực căng trong các cáp dây văng (Hình 3.4). Kết quả xác định lực căng H theo phương pháp đồ thị và so sánh với kết quả tính toán theo phương pháp đã được sử dụng rộng rãi của Hiroshi Zui cho thấy sai số lớn nhất xấp xỉ 6% (Bảng 3.2) là hoàn toàn tin cậy và có thể sử dụng để xác định lực căng trong cáp bằng phương pháp bán thực nghiệm - Phương pháp đồ thị.

Bảng 3.2. Kết quả đo dao động và xác định lực căng trong cáp PM1, PM2, PM3, PM4

 

Hình 3.4: Đồ thị xác định lực căng trong cáp theo phương pháp đồ thị

4. Kết luận

Việc kiểm soát lực căng của cáp dây văng trong giai đoạn khai thác là rất cần thiết để kiểm soát phân bố nội lực trong các cáp và ngăn ngừa sự cố đứt cáp có thể xảy ra. Báo cáo đưa ra một phương pháp mới trong đánh giá lực căng cáp bằng phương pháp bán thực nghiệm - Phương pháp đồ thị (kết hợp giữa lý thuyết và thực nghiệm). Nội dung chính của phương pháp này là xây dựng đường cong lý thuyết của lực căng trong cáp theo các thông số của cáp (phương trình 11 và 12) theo các dạng dao động khác nhau, tiến hành đo lực căng trong cáp bằng phương pháp đo dao động tại hiện trường xác định tần số dao động theo các dạng dao động khác nhau, sau đó tiến hành tra biểu đồ để xác định lực căng trong cáp.

Phương pháp này đã xét đến các ảnh hưởng của độ võng và độ cứng chống uốn của cáp. Phương pháp này cho độ tin cậy cao kiến nghị có thể sử dụng phương pháp này để đánh giá lực căng trong cáp đặc biệt cho các cáp có chiều dài lớn.

Tài liệu thma khảo

[1]. Fujino, Y., and Hoang, N. (2008), Design formulas for damping of a stay cable with a damper, Journal of Structural Engineering, ASCE, 134(2), trang 269 - 278.

[2]. Zui,  H.,  Shinke,  T.,  and  Namita,  Y.  (1996), Practical  formulas  for  estimation  of  cable  tension  by vibration method, Journal of Structural Engineering, ASCE, 122(6), 651 - 656.

[3]. Irvine, H. M (1981), Cable structures, Dover, New York.

[4]. Irvine, H. M., and Caughey, T. K. (1974), The linear theory of free vibrations of a suspended cable, Proc. R. Soc. London, Ser. A, 341, trang 299 - 315.

[5]. Hoang, N., and Fujino, Y., (2007), Analytical study on bending effects in a stay cable with a damper, Journal of Engineering Mechanics, ASCE, 133(11), trang 1241-1246.

[6]. Tabatabai, H., and Mehrabi, A. B. (2000), Design of mechanical viscous dampers for stay cables, J.Bridge Eng., trang 114-123.

[7]. Vietnamese Ministry of Transportation (2009), Technical design of Phú Mỹ Bridge documents.