Xây dựng hệ dẫn đường kết hợp ins/gps sử dụng bộ lọc Kalman kết hợp mô hình sai số ngẫu nhiên tự hồi quy áp dụng cho các đối tượng chuyển động mặt đất

ThS. Triệu Việt Phương Viện Ðo lường Việt Nam PGS. TS. Nguyễn Thị Lan Hương Trường Đại học Bách khoa Hà Nội người phản biện: TS. Thái Trung Kiên TS. Đào Trung Kiên

Tóm tắt: Trong hệ thống dẫn đường quán tính (INS), việc xác định chính xác vị trí của vật thể chuyển động là yêu cầu quan trọng cho mục đích định hướng, điều khiển, giám sát hành trình. Bài báo tập trung trình bày phương án xây dựng hệ INS kết hợp hệ thống định vị toàn cầu GPS sử dụng bộ lọc Kalman kết hợp mô hình hóa sai số ngẫu nhiên trong kết quả đo của các cảm biến bằng mô hình tự hồi quy (autoregressive - AR), nhằm cải thiện độ chính xác trong xác định vị trí các đối tượng chuyển động mặt đất. Dữ liệu được thu thập bằng phần cứng INS/GPS tự chế tạo, kết quả xử lý bằng phần mềm viết trên Matlab cho thấy phương pháp được đề xuất là đúng đắn, giúp nâng cao đáng kể độ chính xác về thông tin vị trí của vật thể sau một khoảng thời gian xác định, hứa hẹn đem đến nhiều kết quả tốt hơn trong các nghiên cứu sắp tới.

Từ khóa: Hệ dẫn đường quán tính, GPS, bộ lọc Kalman, mô hình tự hồi quy - AR.

Abstract: For an inertial navigation system (INS), determining precisely the position of objects in space is a critical requirement for the purposes of navigation, control  and monitoring. This paper focuses on the implementation of an integrated INS/GPS system using Kalman filter combined with stochastic modeling by using autoregressive model (AR), to improve the accuracy in determining the position of land vehicles. The data collected by device developed in this study, and processed by a software written in Matlab showed that the proposed method is correct and significantly improves the accuracy of positioning of the object after a specified time. This promise to deliver better results in the upcoming studies.

Keywords: Inertial navigation system, GPS, Kalman filter, Autoregressive Model.

1. Đặt vấn đề

Trong hệ dẫn đường quán tính (INS), từ gia tốc chuyển động, lấy tích phân hai lần theo thời gian sẽ xác định được vị trí của vật thể. Hệ INS có ưu điểm là cung cấp thông tin vị trí, trạng thái vật thể một cách liên tục và tức thời, có khả năng hoạt động độc lập trong mọi điều kiện khí hậu, thời tiết, địa hình. Tuy nhiên, do sử dụng phép tính tích phân nên hệ INS có thể sinh ra sai số tích lũy theo thời gian, dẫn đến thông tin cung cấp bởi hệ chỉ chính xác trong khoảng thời gian ngắn [1,2]. Để có thể xác định được chính xác vị trí vật thể, cần thiết phải áp dụng những kỹ thuật bù trừ sai số khác nhau. Hiện nay, phương pháp bù trừ sai số phổ biến là kết hợp hệ INS với hệ GPS sử dụng bộ lọc Kalman [1,2,3]. Hệ GPS có tốc độ cung cấp thông tin chậm, tuy nhiên thông tin lại ổn định trong thời gian dài. Kết hợp INS với GPS sử dụng bộ lọc Kalman giúp hệ thống có thể cung cấp được thông tin với tốc độ nhanh, độ ổn định dài, độ chính xác cao [1,2,3]. Với bộ lọc Kalman, việc xây dựng mô hình hệ thống càng chính xác thì kết quả thu được càng tốt. Trong khi đó, quá trình hiệu chuẩn cảm biến chỉ xác định và loại trừ được các sai số hệ thống [4]. Các sai số ngẫu nhiên vẫn tồn tại trong kết quả đo của cảm biến và là nguyên nhân làm giảm chất lượng hệ thống. Vì vậy, phương pháp kết hợp bộ lọc Kalman với mô hình hóa sai số ngẫu nhiên trong kết quả đo của cảm biến bằng mô hình tự hồi quy - AR được đề xuất để hạn chế ảnh hưởng của các sai số ngẫu nhiên.

2. Mô hình hóa sai số ngẫu nhiên của cảm biến sử dụng mô hình tự hồi quy

Sai số ngẫu nhiên tác động vào kết quả đo của cảm biến gồm hai thành phần: Sai số ngẫu nhiên tần số cao có đặc điểm của nhiễu trắng và sai số ngẫu nhiên tần số thấp được đặc trưng bởi nhiễu tương quan. Do các đối tượng mặt đất chuyển động với tần số thấp (từ 0 - 5Hz) [5], nên các sai số ngẫu nhiên tần số cao có thể dễ dàng được loại bỏ bằng bộ lọc Wavelet [2]. Sau khi đã loại bỏ sai số ngẫu nhiên tần số cao, xét đối tượng ở trạng thái đứng yên, mọi biến thiên trong kết quả đo của cảm biến đều do sai số ngẫu nhiên tần số thấp gây ra, sai số này có thể được mô hình hóa bằng các mô hình: Mô hình Gauss-Markov bậc 1, mô hình AR, mô hình MA, mô hình ARMA [2,6]. Trong các mô hình trên, mô hình AR thường được sử dụng hơn cả vì quá trình xác định tham số đơn giản, mô hình xây dựng được có độ chính xác cao, phù hợp với phần lớn các sai số ngẫu nhiên tần số thấp trong thực tế. Mô hình AR bậc p của một tín hiệu ngẫu nhiên có dạng như sau [2,6]:

 

 

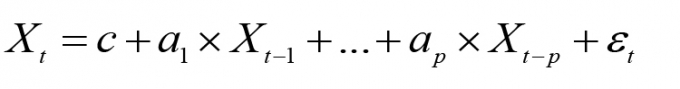Trong đó: X_t- Giá trị của tín hiệu X tại thời điểm t; C- Hằng số; `alpha` ₁ , `alpha` ₂ , ...., `alpha` _p - Các tham số của mô hình; `epsi` _t- Tín hiệu hoàn toàn ngẫu nhiên có phương sai là  `sigma` _`epsi`  ².

3. Thiết kế bộ lọc kalman cho hệ ins/gps

Trong nghiên cứu này, mô hình áp dụng bộ lọc Kalman kết hợp hệ INS và hệ GPS được mô tả như Hình 3.1. Bộ lọc Kalman được dùng để ước lượng vị trí, vận tốc vật thể;, sai số vị trí, sai số vận tốc vật thể . Giá trị sai số vị trí, sai số vận tốc vật thể  được phản hồi để điều chỉnh lại hệ INS. Ưu điểm của mô hình này là đơn giản, khả năng mở rộng và tính kế thừa cao.

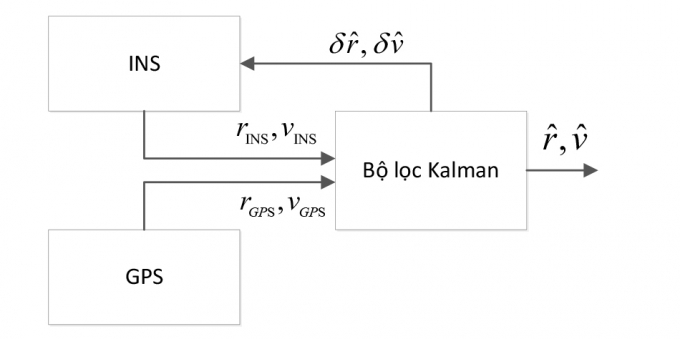Hình 3.1: Mô hình kết hợp INS-GPS sử dụng bộ lọc Kalman

 

Áp dụng phương pháp xây dựng mô hình sai số cho hệ INS được trình bày trong [1,3], thu được mô hình sai số của hệ thống INS dưới dạng mô hình trạng thái như sau:

 

 

 

 

 

 

 

 

 

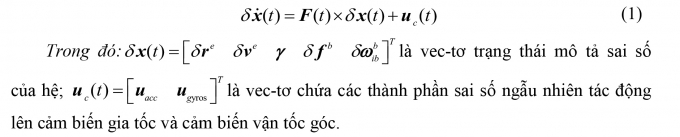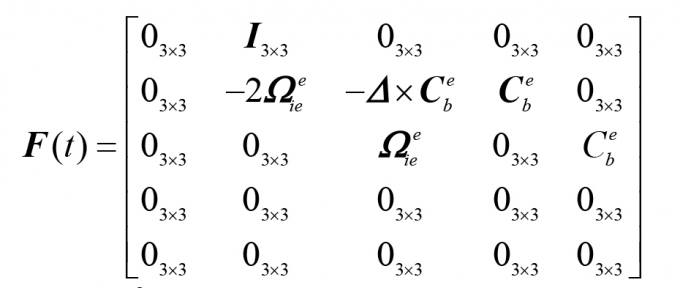Rời rạc hóa phương trình (1) đồng thời áp dụng mô hình AR cho thành phần sai số ngẫu nhiên tác động lên cảm biến gia tốc và cảm biến vận tốc góc thu được hệ phương trình mô tả bộ lọc Kalman như sau:

 

 

 

 

4. Thực nghiệm và kết quả

4.1. Xây dựng phần cứng hệ INS/GPS

Phần cứng hệ INS/GPS sử dụng IMU - LSM9DS0 và mô-đun GPS - Quectel L70. Một số đặc tính kỹ thuật của IMU - LSM9DS0 được mô tả trong Bảng 4.1. Hình ảnh phần cứng được thể hiện trên Hình 4.1. Cảm biến gia tốc trong IMU được hiệu chuẩn theo phương pháp trình bày trong tài liệu tham khảo [4]. Cảm biến vận tốc góc và mô-đun GPS được hiệu chuẩn theo quy trình tại Viện Đo lường Việt Nam.

Bảng 4.1. Đặc tính kỹ thuật cơ bản của khối IMU - LSM9DS0

 4.2. Kết quả thực nghiệm

4.2.1. Mô hình hóa sai số ngẫu nhiên của cảm biến bằng mô hình AR

Hệ thống được đặt ở trạng thái đứng yên, dữ liệu được thu thập ở tần số 100Hz trong 180 giây, sau đó được lọc bằng Wavelet sym4 bậc 4. Dữ liệu sau khi lọc được sử dụng để xác định tham số mô hình AR, tham số nhiễu của bộ lọc Kalman. Độ chính xác và bậc của mô hình AR áp dụng cho các cảm biến được thể hiện trên Hình 4.2.

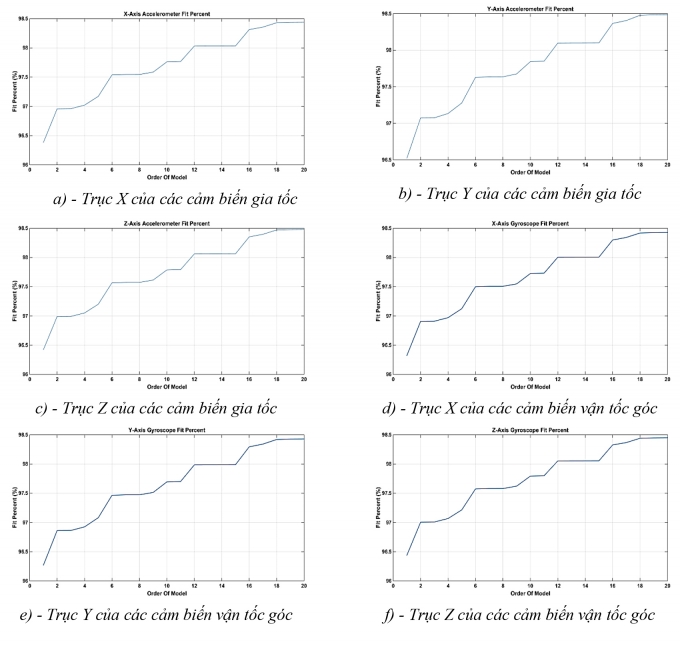Hình 4.2: Độ chính xác và bậc của mô hình AR áp dụng cho cảm biến gia tốc và cảm biến vận tốc góc

 

Các kết quả trong Hình 4.2 cho thấy độ chính xác của mô hình tăng khi bậc của mô hình tăng. Tuy nhiên, khi tăng bậc của mô hình sẽ làm tăng độ phức tạp của mô hình hệ thống. Có thể nhận thấy việc lựa chọn mô hình AR bậc 3 có thể đảm bảo độ chính xác của mô hình ước lượng được, mà không làm phức tạp mô hình hệ thống quá nhiều.

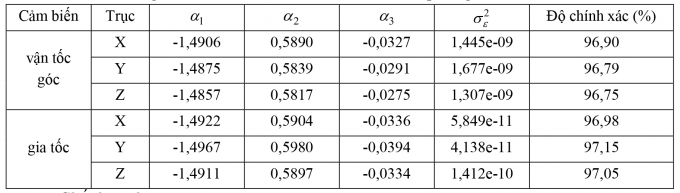
 Tham số của mô hình AR bậc 3 áp dụng cho các cảm biến thể hiện trong Bảng 4.2:

Bảng 4.2. Các tham số của mô hình AR bậc 3 áp dụng cho các cảm biến

 

4.2.2. Chế độ tĩnh

Thiết bị được đặt cố định trong 5 phút, dữ liệu được thu thập ở tần số 100Hz, tần số cập nhật thông tin GPS là 1Hz.  Kết quả xác định vị trí INS khi không kết hợp GPS thể hiện trên Hình 4.3a. Dễ dàng nhận thấy sai lệch vị trí của hệ INS tăng dần theo thời gian. Sau 5 giây, sai lệch vị trí lớn nhất là 0,0489m, sau 3 phút hoạt động sai lệch lớn nhất lên tới 1539,69m. Rõ ràng, INS không thể hoạt động độc lập trong thời gian dài.

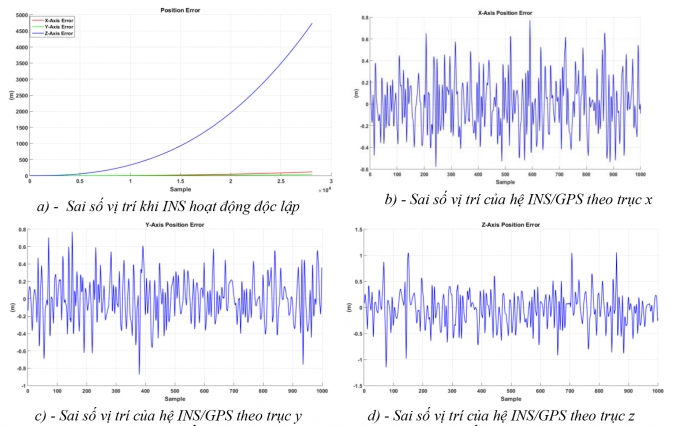Hình 4.3: Sai số vị trí của hệ INS hoạt động độc lập và hệ kết hợp INS/GPS

 

Sai lệch vị trí theo các trục tọa độ của hệ kết hợp INS/GPS sử dụng bộ lọc Kalman kết hợp mô hình hóa sai số ngẫu nhiên của cảm biến bằng mô hình AR với chu kỳ cập nhật là 10s được mô tả trên Hình 4.3b, 4.3c, 4.3d. Sai lệch vị trí trung bình của hệ kết hợp INS/GPS xấp xỉ 1m, giá trị này nhỏ hơn sai số trung bình của GPS. Có thể nhận thấy, việc áp dụng bộ lọc Kalman cho hệ kết hợp INS/GPS đã cải thiện được độ chính xác xác định vị trí của INS khi hoạt động độc lập.

4.2.3. Chế độ động

Thiết bị được lắp cố định trên ô tô, di chuyển trên đường trong khoảng thời gian 30 phút. Dữ liệu được thu thập với tần số 100Hz, tần số cập nhật thông tin GPS là 1Hz. Số liệu thu thập được tính toán và xử lý bằng phần mềm Matlab với chu kỳ cập nhật Kalman là 10s. Quỹ đạo chuyển động của xe xác định bằng INS và hệ kết hợp INS/GPS được thể hiện trên ở Hình 4.4. Dễ dàng nhận thấy quỹ đạo nhận được từ hệ kết hợp INS/GPS (đường màu xanh) bám sát quỹ đạo chuyển động thực (đường màu đỏ) với sai lệch trung bình được nhỏ hơn 3,084m. Rõ ràng, hệ thống này hoàn toàn có thể áp dụng trong việc giám sát, định vị, xác định chính xác vị trí phương tiện chuyển động mặt đất.

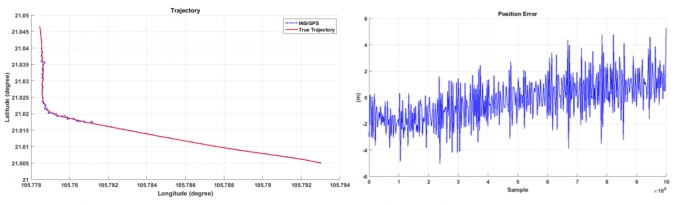Hình 4.4: Quỹ đạo chuyển động thực tế và sai số của hệ INS/GPS

5. Kết luận

Hệ kết hợp INS/GPS sử dụng bộ lọc Kalman kết hợp mô hình hóa sai số ngẫu nhiên bằng mô hình AR cho thấy thông tin về vị trí phương tiện đã được cải thiện đáng kể khi so sánh với hệ INS hay GPS khi hoạt động độc lập. Kết quả trong bài báo sử dụng bộ lọc Kalman 17 trạng thái nhằm kết hợp hệ INS và hệ GPS giúp nâng cao độ chính xác của hệ thống áp dụng được cho vật thể chuyển động mặt đất. Rõ ràng, sự kết hợp INS/GPS áp dụng bộ lọc Kalman kết hợp mô hình hóa sai số ngẫu nhiên bằng mô hình AR là hướng nghiên cứu phù hợp trong bài toán định vị và dẫn đường. Tuy nhiên, để nâng cao hơn nữa độ chính xác trong việc xác định vị trí của vật thể các nghiên cứu tiếp theo sẽ tập trung xây dựng các bộ lọc Kalman nối tầng, tăng các trạng thái quan sát của bộ lọc hoặc kết hợp thêm các hệ thống khác như cao độ kế khí áp…

Tài liệu tham khảo

[1]. David H.Titterton, John L.Weston (2004), Strapdow Inertial Navigation Technology, Michael Faraday House, Peter Peregrimus Ltd.

[2]. Park M (2004), Error Analysis and Stochastic Modeling of MEMS based Inertial Sensors for Land Vehicle Navigation Applications, The University of Calgary.

[3]. Adrian Schumacher (2006), Integration of a GPS aided Strapdown Inertial Navigation System for Land Vehicles, Master of Science Thesis Stockholm, Sweden.

[4]. Triệu Việt Phương, Nguyễn Thị Lan Hương, Trịnh Quang Thông (2015), Xây dựng phương pháp tự hiệu chuẩn cảm biến gia tốc trong hệ dẫn đường quán tính, Tuyển tập Báo cáo khoa học Hội nghị Khoa học Kỹ thuật Đo lường toàn quốc lần thứ VI.

[5]. Tashfeen B. Karamat, Mark D. Eberts, Ahmed El-Shafie (2009), Performance enhancement of MEMS-based INS/GPS integration for low-cost navigation applications, IEEE Trans. Veh. Technol.

[6]. Sameh Nassar (2003), Improving the Inertial Navigation System (INS) Error Model for INS and INS/DGPS Applications, University Of Calgary.