Dao động của ô tô hai cầu theo mô hình hệ không gian 7 bậc tự do

PGS. TS. Vũ Công Hàm  PGS. TS. Vũ Quốc Trụ ThS. NCS. Nguyễn Đình Dũng Học viện Kỹ thuật Quân sự Người phản biện: TS. Vũ Minh Đức PGS. TS. Vũ Đức Lập

Tóm tắt: Bài báo khảo sát dao động của ô tô hai cầu có hệ thống treo phụ thuộc theo mô hình hệ không gian tuyến tính, 7 bậc tự do. Hệ phương trình vi phân dao động và phương pháp tính được đề xuất trong bài báo cho phép khảo sát đầy đủ đáp ứng động lực học của ô tô.

Từ khóa: Dao động, ô tô hai cầu, không gian tuyến tính.

Abstract: This paper considers the response of a two-axled automobile with dependent suspensions in the model of a seven-DOF spatial vibration system. The system of differential equations of vibration and the method proposed for solving allow to investigate fully the dynamic response of the automobile.

Keywords: Oscillator, automotive seals, linear space.

1. Đặt vấn đề

Bài toán khảo sát dao động của ô tô trong quá trình chuyển động trên đường không bằng phẳng nhận được sự quan tâm của nhiều tác giả trong và ngoài nước. Do tính chất phức tạp của việc khảo sát, tính toán, các mô hình không gian về dao động của ô tô mặc dù đã được đề cập nhưng còn khá khiêm tốn. Mô hình hệ dao động không gian 8 bậc tự do của ô tô hai cầu đã được khảo sát trong [3], ở đó tính cản của các lốp xe được bỏ qua, còn thân xe được lập mô hình theo hai khối lượng dao động trong các mặt phẳng vuông góc với trục dọc xe. Trong [5] đã sử dụng mô hình hệ không gian 7 bậc tự do để khảo sát dao động của ô tô hai cầu hệ thống treo độc lập với giảm chấn kiểu khí nén.

Bài báo này sẽ khảo sát dao động của ô tô hai cầu có hệ thống treo phụ thuộc theo mô hình hệ không gian 7 bậc tự do.

2. Mô hình khảo sát dao động

2.1. Một số giả thiết được áp dụng

Bài báo sử dụng các giả thiết sau:

- Các bánh xe luôn tiếp xúc với mặt đường;

- Trong mô hình dao động, thân xe, cầu trước và cầu sau được xem là vật rắn tuyệt đối;

- Coi cản của lốp xe là đàn nhớt tuyến tính;

- Đường tác dụng của lực lò xo và lực giảm chấn thuộc cùng một cụm treo trùng nhau trên một đường thẳng thẳng đứng.

2.2. Mô hình khảo sát

Hình 2.1 biểu diễn một ô tô hai cầu với ba phần tử khối lượng: Thân xe 1, cầu trước 2 và cầu sau 3. Liên kết giữa cầu trước và cầu sau với thân xe được thực hiện thông qua các cụm lò xo, giảm chấn thuộc hệ thống treo của ô tô.

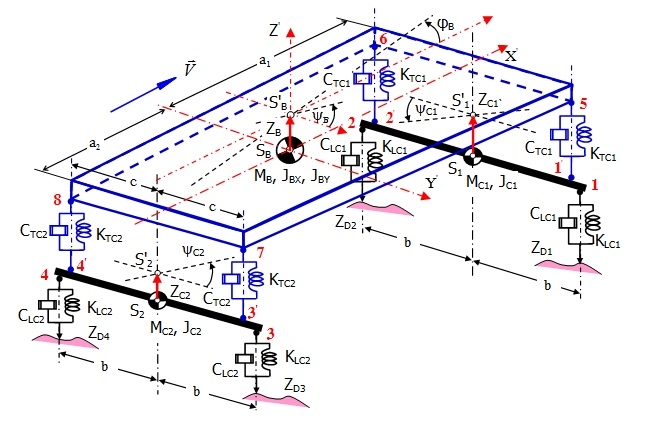Hình 2.1: Mô hình khảo sát dao động của ô tô

Mô hình sử dụng hai hệ tọa độ; hệ cố định OXYZ gắn với mặt đường; hệ động O’X’Y’Z’ gắn với thân xe. Các ký hiệu S, S₁, S₂ - Tương ứng là khối tâm của thân xe, cầu trước và cầu sau; a₁, a₂ - Khoảng cách từ khối tâm thân xe đến trục cầu trước và trục cầu sau; 2b - Khoảng cách trung bình giữa hai vệt bánh xe phải và trái (chiều rộng cơ sở); 2c - Khoảng cách giữa nhíp phải và trái; M_B, M_C1, M_C2 - Tương ứng là khối lượng phần treo, phần không treo cầu trước và cầu sau; J_BX, J_BY - Tương ứng là mô mem quán tính khối lượng của thân xe đối với trục O^’X^’ và O^’Y^’; J_C1, J_C2 - Tương ứng là mô-men quán tính khối lượng của cầu trước và cầu sau với trục song song với trục OX; C_TC1, K_TC1, C_TC2, K_TC2 -  Tương ứng là hệ số đàn hồi và hệ số cản của hệ treo cầu trước và cầu sau; C_LC1, K_LC1,  C_LC2, K_LC2 - Tương ứng là hệ số đàn hồi và hệ số cản của lốp trước và lốp sau.

z_D1, z_D2, z_D3, z_D4 - Độ cao của biên dạng mặt đường tại điểm các lốp xe tương ứng tiếp xúc với mặt đường. Khi biên dạng mặt đường biết trước thì độ cao z_Dk sẽ chỉ phụ thuộc vào vị trí của xe (tọa độ x của khối tâm S)hay:

          (1)

 

Trong các thí dụ tính toán, hàm z_Dk được cho trước, tọa độ x được xác định qua vận tốc chuyển động V và thời gian chuyển động t của xe.

2.3. Các thông số mô tả dao động

Dao động của thân xe và các cầu xe sẽ được khảo sát với các thành phần như sau:

- Thân xe có 3 chuyển động (3 bậc tự do) là: Dịch chuyển thẳng đứng của khối tâm z_B; dịch chuyển góc j_B (góc lắc dọc) quanh trục OY^’;dịchchuyển góc Ψ_B ( góc lắc ngang) quanh trục OX^’.

- Các cầu xe (khối lượng không được treo) có 4 chuyển động là: Dịch chuyển thẳng đứng của khối tâm cầu trước và sau z_C1, z_C2 và dịch chuyển góc Ψ_C1, Ψ_C2 của cầu trước và sau quanh các trục song song với OX.

Quy ước các chuyển vị z_B, z_C1­, z_C2, lấy từ vị trí cân bằng tĩnh, theo đó không cần đề cập đến trọng lượng bản thân các khối lượng dao động.

3. Hệ phương trình vi phân dao động

3.1. Chuyển vị của các điểm gắn lò xo, giảm chấn trên mô hình dao động

Với các bậc tự do nêu trên, có thể thành lập vectơ các tọa độ suy rộng:

      (2)

 

Trên Hình 2.1 biểu diễn vị trí của 12 điểm gắn lò xo và giảm chấn, được đánh số từ 1 đến 8 cho các điểm liên kết thực và bốn điểm liên kết danh nghĩa 1’, 2’, 3’, 4’. Chuyển vị thẳng đứng của các điểm gắn lò xo và giảm chấn được ký hiệu tương ứng là:

   (3)

 

Các chuyển vị thẳng đứng được biểu diễn qua hệ tọa độ suy rộng như sau:

 

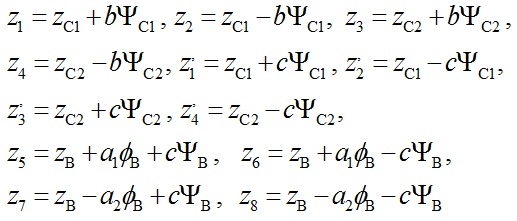              (4)

 

 

 

3.2. Thiết lập hệ phương trình vi phân dao động của cơ hệ

Áp dụng định luật 2 Newton cho 3 khối lượng dao động ta thiết lập được hệ phương trình vi phân dao động của cơ hệ, gồm 7 phương trình vi phân cấp hai như sau:

 

 

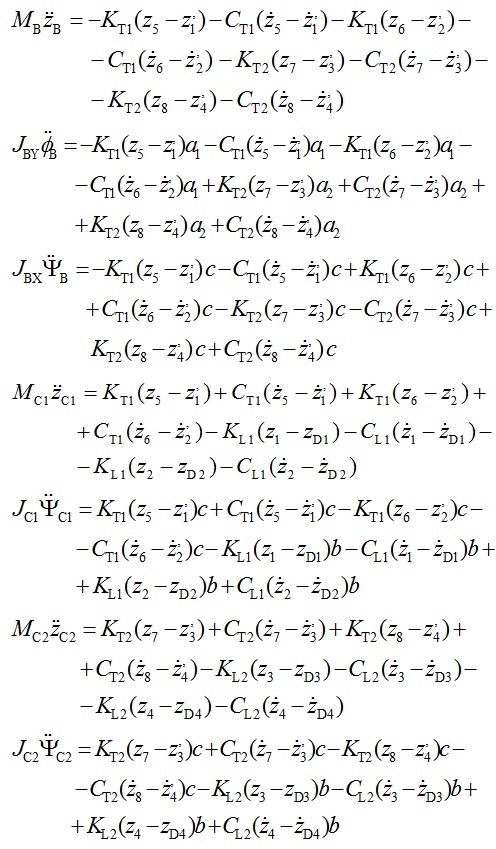      (5)

 

      (6)

 

       (7)

 

       

        (8)

 

        (9)

 

        (10)

 

       (11)

 

 

Thay các biểu thức vào hệ phương trình trên rồi thực hiện một số phép biến đổi đơn giản ta có thể đưa hệ phương trình vi phân dao động ở trên về dạng ma trận, trong đó không có mặt chuyển vị thẳng đứng của các điểm gắn lò xo và giảm chấn, chỉ có mặt các tọa độ suy rộng:

      (12)

 

Trong đó: Ma trận khối lượng [M], ma trận cản [C], ma trận độ cứng [K] và vectơ lực kích thích    

hoàn toàn xác định theo các thông số hình học, động lực học của xe và biên dạng mặt đường.

4. Dao động của ô tô trong hai trường hợp kích thích tiêu biểu

Khảo sát dao động của ô tô dẫn đến việc giải hệ phương trình vi phân dao động tuyến tính theo điều kiện đầu cho trước. Bài viết sử dụng phương pháp số (phương pháp Runge-Kutta) để giải hệ phương trình vi phân dao động bằng cách lập chương trình tính trong phần mềm MATLAB.

Theo đó, đầu tiên cần biến đổi hệ về hệ phương trình vi phân cấp một tương ứng bằng cách đặt  

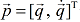 .Khi đó, hệ phương trình vi phân cấp một nhận được có dạng:

 

     (13)

 

Trong đó,         

    - Vectơ đại diện cho vế phải của 14 phương trình vi phân cấp một.

 

Theo (13) có thể thấy 7 thành phần đầu của                                

    là `vecp`   , 7 thành phần còn lại là biểu thức của   `vecp`

được rút ra từ hệ phương trình (5) `-:`  (11) bằng cách chia các vế phải cho hệ số của gia tốc suy rộng tương ứng

Dưới đây trình bày kết quả tính toán trong hai trường hợp tiêu biểu về kích thích. Giá trị của các thông số hình học và động lực học được lấy theo xe GAZ-66 [4]:

M_B=2200 kg; M_C1=660 kg; M_C2=580kg; J_BX=756kg.m²; J_BY=2750kg.m²; J_C1=1780kg.m²; J_C2=1170kg.m²; K_T1=246000 N/m;K_T2=196000N/m; C_T1=1500kg/s; C_T2=1500kg/s; K_L1=800000N/m; K_L2=800000N/m; C_L1=62000kg/s; C_L2=62000kg/s; a₁=1,563m; a₂=1,737m; 2b=1,8m; 2c=1,2m.

Trường hợp 1: Xe chuyển động với vận tốc không đổi V  trên mặt đường có biên dạng hình sin (Hình 4.1).

Biên độ h và bước sóng L của biên dạng mặt đường cho hai bánh bên trái được ký hiệu là (h_T, L_T), cho hai bánh bên phải là (h_P, L_P).

Phương trình mô tả chiều cao mấp mô tại điểm tiếp xúc của bốn bánh xe với mặt phẳng danh nghĩa của đường (trục Ox trên Hình 2.1) trong trường hợp này là:

 

(14)

 

 

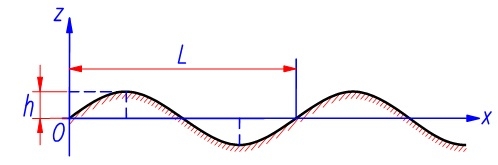Hình 4.1: Biên dạng mặt đường hình sin

Trong các công thức (14), x = Vt  là tọa độ theo phương x của khối tâm S của thân ô tô tại thời điểm t. Giá trị cụ thể của các thông số về biên dạng mặt đường được sử dụng để tính toán là:

V = 20km/h; h_P = 15mm; h_T = 25mm;

L_P = 5,0m; L_T = 5,0m.

Các điều kiện đầu là: 

 

 

Hình 4.2 là các đồ thị biểu diễn ba thành phần dao động thẳng đứng của thân xe (z_B = z_B(t)), cầu trước (z_C1 = z_C1(t)) và cầu sau (z_C2 = z_C2(t)).

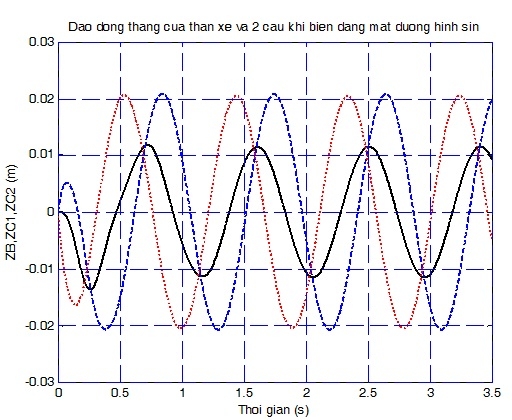Hình 4.2: Dao động thẳng đứng của thân xe và hai cầu khi biên dạng mặt đường hình sin (zB - nét liền, zC1 - nét đứt, zC2 - chấm chấm)

 

Các đồ thị Hình 4.2 cho thấy, với dạng kích thích đang xét, ba thành phần dao động thẳng đứng ở giai đoạn sau quá độ cũng có dạng hình sin và hoàn toàn phù hợp với lý thuyết. Đồ thị mô tả các thành phần dao động góc (không trình bày ở đây) cũng có dạng tương tự.

Trường hợp 2: Xe đang chạy với vận tốc không đổi V trên đường bằng phẳng thì đụng phải một mô đất trên vệt bánh xe bên phải, nơi hai bánh xe số 1 và số 3 đi qua. Sau đó một khoảng bằng d theo hướng chuyển động, xe lại đụng phải một mô đất khác trên vệt bánh xe bên trái, nơi bánh xe số 2 và bánh xe số 4 đi qua.

Sự thay đổi chiều cao của hai mô đất theo phương chuyển động được mô tả theo hàm sin với giá trị lớn nhất là h_p và h_T , chiều dài tương ứng của hai mô đất theo phương chuyển động là L_p  và  L_T (Hình 4.3). Ngoài hai mô đất đó, mặt đường lại hoàn toàn bằng phẳng. Trong trường hợp riêng, khi xe chỉ đụng phải một mô đất trên một vệt bánh xe, chỉ cần lấy h_p = 0 hoặc h_T = 0.

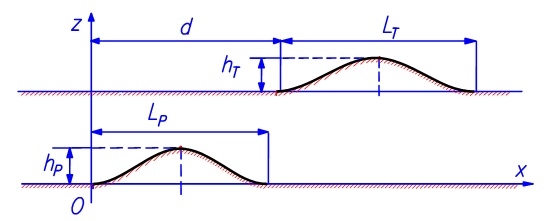Hình 4.3: Biểu diễn biên dạng và vị trí tương đối của hai mô đất trên hai vệt bánh xe

 

Các giá trị số được sử dụng để tính toán là:

V = 25km/h,  h_p = 35mm, h_T = 25mm

L_P = 65cm, L_T= 80cm, d = 5m

Các điều kiện đầu:

 

 

Hình 4.4 là đồ thị mô tả sự thay đổi theo thời gian của hai thành phần dao động góc của thân xe ϕ_B=ϕ_B(t), Ψ_B = Ψ_B(t).

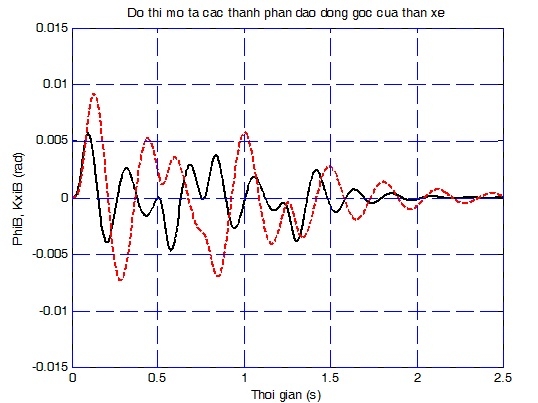Hình 4.4: Đồ thị mô tả hai thành phần dao động góc của thân xe (ϕB - nét liền, ΨB - nét đứt)

Các đồ thị cho thấy, dạng kích thích đang xét có ảnh hưởng lớn hơn đối với thành phần dao động góc ngang xe, điều này là phù hợp với thực tế. Do có mặt của các giảm chấn nên hai dao động góc ở trên đều là dao động tắt dần. 5 thành phần dao động còn lại của cơ hệ cũng được xác định một cách đồng thời với hai thành phần dao động góc nêu trên và có thể được biểu diễn theo cách tương tự.

5. Kết luận

Bài báo đã xây dựng mô hình dao động dạng không gian, 7 bậc tự do của ô tô hai cầu, có hệ thống treo phụ thuộc, chịu kích thích động học khi chuyển động thẳng trên mặt đường với vận tốc không đổi, đã thiết lập hệ phương trình vi phân dao động của cơ hệ và chỉ ra phương pháp giải hệ phương trình vi phân dao động bằng phương pháp số nhằm tìm đáp ứng dao động của cơ hệ theo tất cả các bậc tự do. Bài báo cũng mô tả hai dạng kích thích động học khá tiêu biểu thường được áp dụng trong tính toán dao động của ô tô, đã xây dựng chương trình tính toán và giới thiệu một vài kết quả tiêu biểu ở dạng đồ thị nhằm minh họa tính khả thi của phương pháp. Với hệ phương trình vi phân dao động nhận được, có thể xác định các tần số dao động riêng và các dạng dao động riêng của ô tô bằng phương pháp giải tích. Chương trình tính đã xây dựng được cho phép khảo sát kỹ lưỡng hơn dao động của ô tô khi chuyển động trên mặt đường không bằng phẳng. 

Tài liệu tham khảo

[1]. Vũ Công Hàm, Trần Văn Bình (2014), Lý thuyết dao động, NXB. Quân đội nhân dân, Hà Nội.

[2]. Vũ Công Hàm, Trần Quang Dũng (2007), Dao động cơ học, Học viện Kỹ thuật Quân sự.

[3]. Vũ Đức Lập (2011), Dao động ô tô, NXB. Quân đội nhân dân, Hà Nội.

[4]. Vũ Đức Lập (2004), Sổ tay tra cứu tính năng kỹ thuật ô tô, Học viện Kỹ thuật Quân sự.

[5]. CHEN Ke, ZHANG Ming, TONG Xuefeng, Vibration characteristic analysis of vehicle air suspension based on fuzzy control, The second International Conference on Electronic & Mechanical Engineering and Information Technology (EMEIT-2012), pp. 2196-2199, Published by Atlantis Press, Paris, France.