Lựa chọn vị trí tối ưu đặt điểm đo dao động phục vụ công tác đo đạc dao động cầu treo dây văng

TS. Bùi Tiến Thành KS. Lê Thanh Tùng Trường Ðại học Giao thông vận tải Ths. Lê Hoàng Minh Quỹ Bảo trì đường bộ Trung ương Người phản biện: TS. Đỗ Anh Tú

TÓM TẮT: Hiện nay, nhiều công trình cầu dây văng lớn tại Việt Nam đã và đang được đầu tư xây dựng do có ưu điểm vượt trội về vượt nhịp lớn và chiều cao kiến trúc thấp mang lại. Tuy nhiên, sau thời gian khai thác, sử dụng, các cây cầu này cần được kiểm tra, kiểm định đánh giá chất lượng, một trong các phương pháp kiểm định đánh giá cầu là phương pháp đo dao động. Để nhận dạng được dao động của kết cấu cầu dây văng nhịp lớn thì số liệu thu thập được phải đầy đủ bằng cách bố trí các điểm đo hợp lý nhằm thu thập được nhiều thông tin nhất. Hiện nay, các điểm đo được bố trí chủ yếu dựa vào kinh nghiệm của tư vấn kiểm định. Nội dung chính của bài báo tập trung phân tích một phương pháp lựa chọn tối ưu vị trí đặt điểm đo dao động cầu treo dây văng. Các vị trí tối ưu này được xác định bằng phương pháp en-tro-pi thông tin. Kết quả của nghiên cứu sẽ được ứng dụng vào đo đạc công trình cầu Mỹ Thuận.

TỪ KHÓA: Bố trí điểm đo tối ưu, cầu treo dây văng, cầu Mỹ Thuận, dao động kết cấu cầu, en-tro-pi thông tin, quan trắc, theo dõi thường xuyên.

Abstract: Over the past years, many long span cable-stayed bridges have been built in Vietnam. This bridge type has competitive advantages of spanning long distance and slenderness. After many years in operation, the need for maintenance and periodic condition assessment leading to permanent monitoring arises. The method of vibration based assessment has proved reliable as it is a global meanwhile non-destructive method, which requires a comprehensive field test in operational condition. In this test, the location of sensors is often decided by experience. This paper proposes a methodology of optimal sensor placement based on information entropy index. As an example, the modal test of the My Thuan bridge is presented.    

Keywords: Optimal sensor placement, optimal sensor location, cable-stayed bridge, my thuan bridge, vibration of bridges, information entropy, permanent monitoring.

1. ĐẶT VẤN ĐỀ

Hiện nay, các công trình giao thông tại Việt Nam đang được xây dựng với số lượng lớn nhằm đáp ứng kịp thời với nhịp độ phát triển của nền kinh tế. Do đó, chất lượng khai thác của công trình cũng được xem xét một cách thỏa đáng. Việc nghiên cứu các phương pháp kiểm định, thử nghiệm công trình trong giai đoạn khai thác mang ý nghĩa đặc biệt quan trọng. Kết quả thu nhận được là một bức tranh tổng thể về ứng xử của công trình cầu là cơ sở quan trọng cho việc đưa ra các đánh giá về khả năng khai thác phục vụ của công trình. Phương pháp kiểm định, thử nghiệm kết cấu công trình cầu bằng phương pháp đo dao động được nhiều quan tâm trong thập kỷ qua, do sự phát triển mạnh mẽ của máy móc, thiết bị đo đạc và các kỹ thuật nhận dạng dao động tiên tiến. Đặc biệt chú ý là phương pháp đo và nhận dạng dao động hiện trạng khai thác trong điều kiện cầu thông xe bình thường do tính hiệu quả từ việc không phải dừng xe và phương tiện trong quá trình đo.

Gần đây, Bộ GTVT đã có nhiều quan tâm đến công tác kiểm định và thử nghiệm kết cấu cầu bằng phương pháp động cho các công trình cầu lớn được xây dựng trong hệ thống quốc lộ Việt Nam. Nhiều công trình cầu dây văng lớn đã đưa vào khai thác như Mỹ Thuận [1], Cần Thơ, Cầu Kiền, Bãi Cháy, Nhật Tân… đã được kiểm định, thử nghiệm bằng phương pháp đo dao động. Tuy nhiên hiện nay, việc bố trí vị trí các điểm đo dao động giữa các cầu là rất khác nhau, dựa chủ yếu vào kinh nghiệm của tư vấn kiểm định. Nhiều vị trí bố trí đầu đo là không cần thiết dẫn đến hiệu quả đo đạc không cao. Do đó, nghiên cứu về một phương pháp nhằm đưa ra được vị trí tối ưu đặt điểm đo dao động mang lại một ý nghĩa rất lớn và đặc biệt quan trọng đối với công tác kiểm định, thử nghiệm công trình cầu ở Việt Nam.

2. NGHIÊN CỨU XÂY DỰNG THUẬT TOÁN TỐI ƯU BẰNG PHƯƠNG PHÁP EN-TRO-PI

2.1. Cơ sở lý thuyết của phương pháp en-tro-pi

Sau khi mô hình hóa kết cấu bằng phương pháp phần tử hữu hạn (PTHH), một mạng lưới các điểm đo đã được hình thành. Trong hầu hết các trường hợp, số lượng các bộ cảm biến là không đủ để trang bị cho toàn bộ các vị trí điểm đo cùng một lúc. Vì vậy, thuật toán tối ưu hóa điểm đo là cách xác định các vị trí tối ưu bố trí các đầu đo vào các vị trí có thể đặt điểm đo.

Một trong những phương pháp phổ biến nhất để lựa chọn vị trí cảm biến tối ưu là dựa trên những lý thuyết thông tin giảm thiểu đến giới hạn các thông tin không cần thiết của ma trận thông tin Fisher (FIM) trong thống kê Bayes [2]. Trong thực tế, phương pháp này thường được sử dụng để xác định lưới bố trí điểm đo đo dựa trên lựa chọn một hàm mục tiêu hợp lý.

Giả sử y_k là véc-tơ thông số các dữ liệu đo được (dữ liệu đầu ra) với k là chỉ số thời gian của các mẫu đo rời rạc; F là ma trận các dạng mode dao động được xác định từ mô hình PTHH mô phỏng cầu; x_k là tọa độ hình thức của mô hình này và e_k là tổng hợp sai số do mô hình và sai số của kết quả đo đạc. Quan hệ giữa tọa độ dạng modes của mô hình và số liệu đo được thực tế thỏa mãn phương trình sau:

 

 

Ở đó, L là ma trận vị trí bao gồm các toán tử 0 và 1 để liên hệ giữa ma trận các bậc tự do đo thực tế và các bậc tự do của mô hình PTHH. Chọn vị trí tối ưu bố trí các điểm đo chính là xác định ma trận L để giá trị en-tro-pi thông tin của ma trận tọa độ hình thức x_k là nhỏ nhất. Hay nói cách khác, ma trận thông tin Fisher của x_k (là hàm của biến L) là tối đa:

 

Trong đó: Σ - Ma trận thống kê hiệp biến của e_k; Q(L; S) - Một ma trận xác định các thông tin hữu ích được biết nhờ ma trận thông tin Fisher (FIM). Vị trí bố trí điểm đo tối ưu là một tập hợp những thông tin hữu ích đã được hạn chế tối đa các chỉ số thông tin dữ liệu ngẫu nhiên bằng phương pháp en-tro-pi. Ma trận L cho kết quả vị trí các điểm đo tối ưu một cách rõ ràng. Với số lượng các bộ cảm biến (hay chính xác hơn số lượng các bậc tự do dự định đo) được lựa chọn thì một cấu hình tối ưu để bố trí điểm đo sẽ được thiết lập.

Một thông số quan trọng của phương pháp là chỉ số en-tro-pi thông tin (IEI). Chỉ số en-tro-pi thông tin là giá trị ước lượng tương đối so với cấu hình cảm biến đầy đủ. Chỉ số này được xác định bằng công thức:

 

 

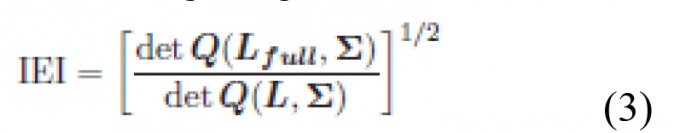Với L_full là ma trận với các vị trí có thể bố trí các cầu đo theo mô hình.

2.2. Thuật toán bố trí điểm đo tối ưu

2.2.2. Thuật toán tuần tự thuận FSSP

2.2.2.1. Khởi tạo: Không có cảm biến được chọn, số lượng của cảm biến N = 0 và cấu hình cảm biến L_N = {}.

2.2.2.2. While số lượng của các cảm biến N < số lượng tối đa của bộ cảm biến N₀ do:

- Xem xét kết hợp với việc bổ sung một cảm biến, N = N + 1;

- For đếm số lượt i = 1 to số lượng vị trí cảm biến có thể N_d = N + 1:

+ Có được cấu hình L_N bằng các thêm cảm biến i vào cấu hình L_N-1;

+ Đánh giá các thông tin dữ liệu ngẫu nhiên của cấu hình cảm biến mới L_N.

- Kết thúc;

- Chọn cấu hình cảm biến L_N mà các thông tin dữ liệu ngẫu nhiên đã được giảm thiểu.

2.2.2.3. Kết thúc

2.2.3. Thuật toán tuần tự nghịch BSSP

2.2.3.1. Khởi tạo: Tất cả các cảm biến đều được chọn, số lượng của cảm biến N = N_d và cấu hình của cảm biến L_N.

2.2.3.2. While số lượng của cảm biến N > 1 do:

- Xem xét kết hợp với việc loại bỏ một cảm biến, N = N - 1;

- For đếm số lượt i = 1 to số lượng các cảm biến có thể được loại bỏ N + 1:

+ Có được cấu hình L_N bằng cách loại bỏ cảm biến i từ cấu hình L_N+1;

+ Đánh giá các thông tin dữ liệu ngẫu nhiên của cấu hình cảm biến mới L_N.

- Kết thúc;

- Chọn cấu hình cảm biến L_N mà các thông tin dữ liệu ngẫu nhiên đã được giảm thiểu.

2.2.3.3. Kết thúc

3. ÁP DỤNG THUẬT TOÁN TÌM ĐIỂM ĐO DAO ĐỘNG TỐI ƯU CẦU MỸ THUẬN PHỤC VỤ CÔNG TÁC ĐO ĐẠC THỰC TẾ

3.1. Cơ sở xây dựng mô hình PTHH cầu Mỹ Thuận

Để thiết kế mạng lưới các điểm có thể bố trí điểm đo và lập kế hoạch để thực hiện phép đo, phương pháp PTHH đã được xây dựng dựa trên các yếu tố hình học từ quá trình khảo sát đến kiểm định kết cấu. Dầm dọc được mô hình bằng phần tử dầm không gian 2 nút. Phần tử dầm này có 6 bậc tự do tại mỗi nút, bao gồm 3 chuyển vị theo phương x, y, z và 3 góc xoay quanh trục x, y, z trong hệ trục tọa độ. Dầm ngang được mô hình bằng phần tử dầm không gian 2 nút giống như dầm dọc. Mỗi dầm ngang được chia thành 2 phần tử có chiều dài bằng nhau. Bản mặt cầu được mô hình bằng phần tử bản 4 nút.  Phần tử này có 6 bậc tự do tại mỗi nút bao gồm 3 chuyển vị theo phương x, y, z và 3 góc xoay quanh trục x, y, z trong hệ tọa độ.

Trên thực tế, bản mặt cầu được liên kết cứng với các dầm chủ và dầm ngang, do đó trong mô hình PTHH này, các phần tử tấm được liên kết cứng với các dầm chủ, được mô hình bằng phần tử tấm có 4 nút liên kết cứng thuộc phần tử dầm dọc và dầm ngang. Tháp cầu được mô hình bằng phần tử dầm không gian 2 nút giống như dầm dọc cầu và dầm ngang. Phần phía trên tháp mặt cắt không thay đổi, được chia thành 17 phần tử dầm tại những điểm neo cáp. Phần thân tháp phía dưới mặt cắt thay đổi theo chiều cao. Trong mô hình PTHH, mặt cắt tháp được vuốt từ dưới lên trên. Giữa 2 xà ngang dầm được chia thành 10 phần tử dầm chiều dài như nhau. Chân tháp phía dưới xà ngang được chia thành 5 phần tử dầm. Cáp dây văng của cầu được mô hình bằng phần tử dầm 2 đầu nút. Mỗi dây văng là 1 phần tử, liên kết với tháp và dầm chủ là liên kết cứng. Trong mô hình PTHH, nút phía trên của cáp được nối cứng đó chính là nút của phần tử tháp, nút phía dưới được liên cứng với nút thuộc phần tử dầm chủ liên kết cứng chống chuyển vị theo 3 phương x, y, z và 3 góc xoay quanh trục x, y, z trong hệ tọa độ.

Hệ trục tọa độ được lựa chọn sao cho trục X là trục theo hướng dọc cầu; trục Y là trục theo hướng ngang cầu - ngược chiều với hướng dòng chảy của sông và trục Z là theo hướng thẳng đứng.

Hình 3.1: Mô hình hóa kết cấu cầu Mỹ Thuận

 

Sau khi mô hình hóa kết cấu và phân tích dao động hình thức sẽ thu được các dạng dao động của kết cấu cầu (theo phương ngang cầu và theo phương đứng) với các tần số dao động tương ứng được sắp xếp từ nhỏ đến lớn.

Bảng 3.1. Tần số của 20 mode dao động của cầu Mỹ Thuận sau khi mô hình

STT	Tần số	STT	Tần số	STT	Tần số	STT	Tần số
	(Hz)		(Hz)		(Hz)		(Hz)
1	0.186	6	0.547	11	0.699	16	0.903
2	0.299	7	0.549	12	0.718	17	0.938
3	0.376	8	0.594	13	0.843	18	0.961
4	0.442	9	0.601	14	0.852	19	0.967
5	0.492	10	0.66	15	0.901	20	0.982

Hình 3.2: Dạng mode dao động cầu Mỹ Thuận

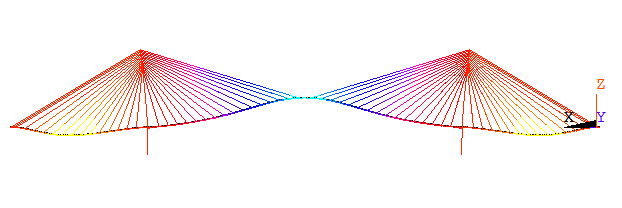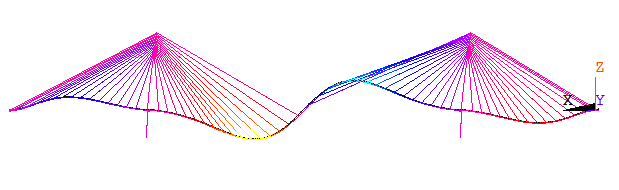Hình 3.2: Dạng mode dao động cầu Mỹ Thuận

 

3.2. Kết quả vận dụng thuật toán

Từ mô hình PTHH, vị trí bố trí các điểm đo được dự kiến bố trí ở cả dầm và trên tháp cầu ở cả 2 bên mặt phẳng dây và các vị trí khác như giữa nhịp, trên vị trí gối cầu ở tháp với tổng cộng 262 điểm đo. 

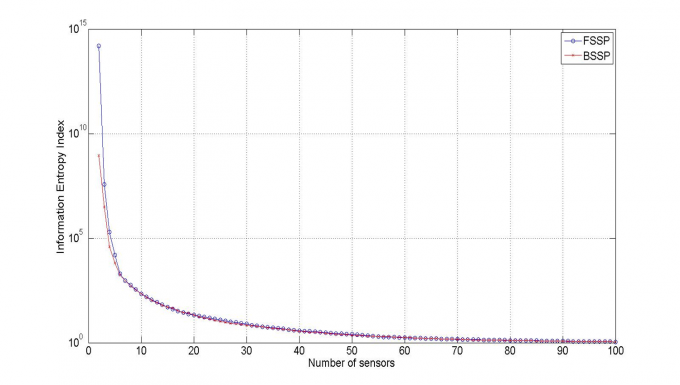Hình 3.3: Biểu đồ quan hệ giữa số lượng điểm đo và chỉ số IEI tối ưu

Kết quả phân tích cho thấy với 80 điểm đo có thể được bố trí chỉ số en-tro-pi thông tin IEI đã tiệm cận đến giá trị đơn vị. Từ đó, nếu có thể bố trí 100 điểm đo ngoài thực tế ta có thể xác định được tất cả các mode dao động như bài toán mô hình. Nếu thực tế bố trí số lượng đầu đo nhỏ hơn 10 thì lượng thông tin có ích thu được là rất ít, rất khó có khả năng nhận dạng được trạng thái dao động của cầu, đặc biệt là các mode dao động ngang và mode dao động xoắn.

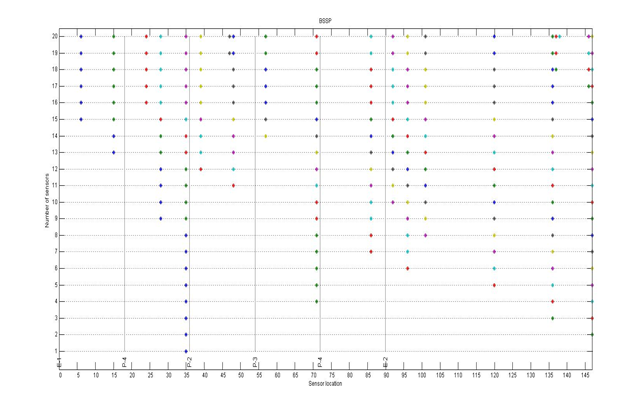Hình 3.4: Vị trí các điểm đo tối ưu với số lượng đầu đo tăng dần

Sau khi có được kết quả chỉ số en-tro-pi thông tin thuật toán xác định cho ta ma trận vị trí L bố trí điểm đo tối ưu sao cho khi bố trí điểm đo tại vị trí đó các thông tin nhận được là nhiều nhất. Ứng với số lượng đầu đo có thể huy động, ma trận L là cơ sở để bố trí các điểm đo dao động thực  tế ngoài hiện trường.

4. KẾT LUẬN

Kết quả nghiên cứu đã đưa ra phương pháp lựa chọn số lượng điểm đo phù hợp và vị trí tối ưu bố trí các điểm phục vụ đo đạc dao động cầu dây văng ngoài hiện trường, thay vì việc phải bố trí rất nhiều điểm đo để có được dữ liệu, thông số kỹ thuật cần thiết mới nhận dạng được dao động cầu dây văng thì nay chúng ta chỉ phải bố trí lắp đặt cảm biến đo ở một số vị trí nhất định. Việc chọn được vị trí tối ưu để bố trí các điểm đo dao động cầu dây văng sẽ làm giảm lượng công việc đồ sộ bằng việc giảm số lượng bố trí các điểm đo, do đó không yêu cầu đường truyền và băng thông quá lớn khi chuyển các dữ liệu về máy chủ, giảm được rất nhiều chi phí và thời gian thực hiện đo đạc dao động cầu dây văng.

Tài liệu tham khảo

[1]. Công ty TNHH GTVT và Công ty Cổ phần Tư vấn đầu tư và Xây dựng công trình giao thông (2016), Báo cáo kiểm tra chi tiết dây văng cầu Mỹ Thuận, QL1A, tỉnh Tiền Giang và Vĩnh Long.

[2]. C. Papadimitriou, G. Lombaert (2012), The effect of prediction error correlation on optimal sensor placement in structural dynamics, Mechanical Systems and Signal Processing 28,  105-127.

[2]. J.L. Beck, L.S. Katafygiotis (1998), Updating models and their uncertainties-I: Bayesian statistical framework, Journal of Engineering Mechanics (ASCE) 124 (4) 455-461.

[3]. L.S. Katafygiotis, C. Papadimitriou, H.F. Lam (1998), A probabilistic approach to structural model updating, International Journal of Soil Dynamics and Earthquake Engineering 17, (7-8) 495-507.