Phân tích động lực học dầm có vết nứt trên nền đàn hồi chịu tác dụng của khối lượng di động

PGS. TS. Nguyễn Thái Chung  KS. Lê Phạm Bình Trường Ðại học Kỹ thuật Lê Quý Ðôn ThS. Nguyễn Thị Hồng Trường Ðại học Thủy Lợi Người phản biện: GS.TS. Hoàng Xuân Lương GS.TSKH. Nguyễn Tiến Khiêm Người phản biện: GS.TS. Hoàng Xuân Lượng GS.TSKH. Nguyễn Tiến Khiêm

TÓM TẮT: Bài báo trình bày thuật toán phần tử hữu hạn (PTHH), chương trình tính trong môi trường Matlab nhằm phân tích động lực học dầm có vết nứt hở trên nền đàn hồi, chịu tác dụng của khối lượng di động. Khảo sát số với các thông số vết nứt, nền và tải trọng thay đổi, cho thấy mức độ ảnh hưởng của chúng đến đáp ứng động của dầm. Kết quả của bài báo là cơ sở cho việc phân tích, đánh giá và chẩn đoán các hư hỏng của kết cấu dầm trên nền đàn hồi chịu tác dụng của tải di động, trong đó các khuyết tật thường gặp của dầm như vết nứt được xem xét nhằm nâng cao hiệu quả làm việc của hệ, ứng dụng trong các lĩnh vực kỹ thuật: GTVT, xây dựng…

TỪ KHÓA: Dầm có vết nứt, nền đàn hồi, khối lượng di động.

Abstract: This paper presents a finite element algorithm, the calculation program in the Matlab environment for dynamics analysis of cracked beams on elastic foundation under moving mass. Quantity surveying with parameters of varied cracks, foundation and loads show their influence level on the dynamic response of the beams. The findings of the paper is the basis for the analysis, evaluation and diagnosis of damages of beam structure on the elastic foundation subjected to moving loads, in which the common defects of the beams such as cracks are reviewed in order to improve the system’s operational efficiency, applying in technical areas: transportation, construction, etc.

Keywords: Cracked beam, elastic foundation, moving mass.

1. ĐẶT VẤN ĐỀ

Kết cấu dạng dầm trên nền đàn hồi, đàn nhớt thường được mô hình hóa để tính toán các kết cấu công trình đường sắt. Trong quá trình sử dụng, do nhiều nguyên nhân khác nhau có thể gây ra các khuyết tật giảm yếu cho dầm, một trong những dạng đó là các vết nứt. Vết nứt xuất hiện làm giảm khả năng chịu lực của dầm, dẫn đến nguy cơ hư hỏng công trình. Salih N Akour [1] phân tích động lực học phi tuyến của dầm trên nền đàn hồi chịu tác dụng của lực phân bố đều di động bằng phương pháp giải tích. Cũng bằng phương pháp gải tích S. T. Oni và T. O. Awodola [2], Karmir Tiwari, Ramakrishna Kuppa [3] phân tích động lực học của dầm Bernoulli - Euler trên nền đàn hồi chịu tác dụng của khối lượng di động. Murat. R và Yasar. P [4] phân tích dao động của dầm công xôn có vết nứt, chịu tác dụng của khối lượng di động. Sử dụng phương pháp giải tích, Animesh C. và Tanuja S. V. [5] phân tích động lực học của dầm có vết nứt, chịu tác dụng của khối lượng di động. Mattar et al [6] phân tích động lực học của dầm có vết nứt trên nền đàn hồi chịu tác dụng của tải trọng điều hòa di động bằng phương pháp giải tích, trên cơ sở sử dụng mô hình dầm Timoshenko. Nguyễn Thái Chung, Nguyễn Trang Minh, Lê Phạm Bình [7] sử dụng phương pháp PTHH phân tích động lực học dầm có vết nứt, chịu tác dụng của khối lượng di động. Cho đến nay, việc phân tích động lực học của dầm trên nền đàn hồi chịu tác dụng của tải trọng di động (khối lượng, lực) đã có nhiều công bố, còn đối với dầm có vết nứt trên nền đàn hồi chịu tải trọng di động đã có một số nghiên cứu, nhưng chủ yếu sử dụng phương pháp giải tích, hạn chế của cách tiếp cận này là kết cấu dầm và tải trọng tác dụng đơn giản. Trên cơ sở phương pháp PTHH, các tác giả phân tích động lực của dầm trên nền đàn hồi chịu tác dụng của khối lượng di động. Khảo sát số, xem xét ảnh hưởng của nền đàn hồi, tốc độ tải trọng, vị trí vết nứt đến đáp ứng động của dầm.

2. MÔ HÌNH BÀI TOÁN VÀ CÁC GIẢ THIẾT

Xét dầm dài hữu hạn đặt trên nền đàn hồi được mô tả bởi hệ lò xo đàn hồi theo 2 phương vuông góc với trục dầm, có độ cứng k_a và phương dọc trục dầm có độ cứng k_t, dầm có vết nứt hở, dạng chữ V. Khối lượng m di chuyển dọc trục dầm với vận tốc v (Hình 2.1).

Hình 2.1: Mô hình bài toán

 

3. CÁC PHƯƠNG TRÌNH CHỦ ĐẠO

3.1. Ma trận độ cứng và ma trận khối lượng của dầm có vết nứt chịu uốn

Xét phần tử dầm hai điểm nút, có vết nứt, mỗi nút gồm hai bậc tự do: Chuyển vị đứng y_i, góc xoay θ_i (i=1,2) (Hình 3.1).

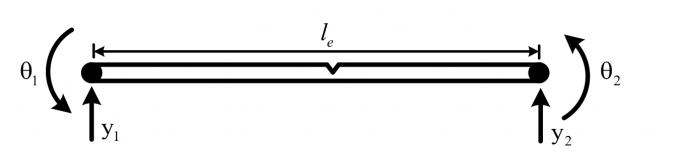Hình 3.1: Phần tử dầm hai điểm nút, có vết nứt

 

Véc-tơ chuyển vị nút phần tử: { q^e} = { y₁     ` ` ₁         y₂         ` ` ₂}

Ma trận độ cứng [K_c^e] của phần tử được xác định bởi [5], [7]:

[K_c^e] = [Ke] - [K_C]  (1)

Trong đó:  [K_e] - Ma trận độ cứng phần tử dầm không có vết nứt; [K_C]- Ma trận độ cứng phần tử dầm suy giảm do vết nứt, các ma trận trên được xác định:

 

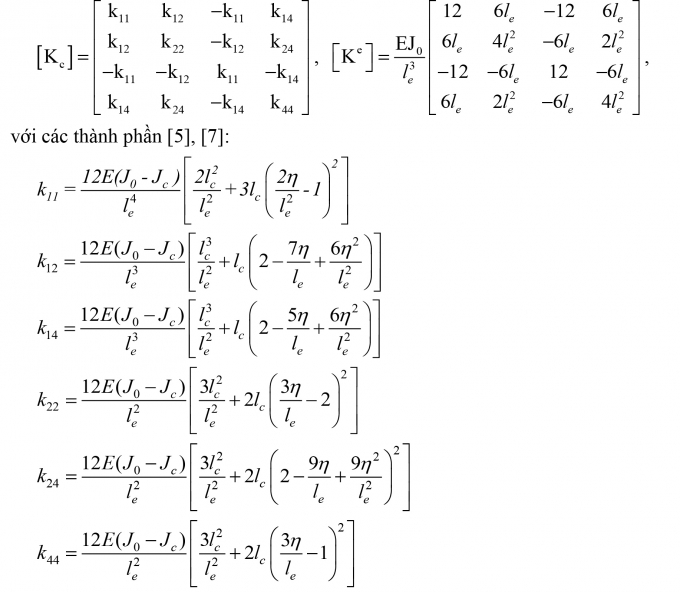 (2)

 

 (3)

(4)

(5) 

 (6)

 

 (7)

 (8)

 

 

 

Trong đó: J₀, J_c - Tương ứng là mô-men quán tính của mặt cắt ngang dầm đối với trục Oz tại vị trí không có vết nứt và tại vị trí có vết nứt; l_c = 1,5d (d - Độ sâu vết nứt), l_e - Chiều dài phần tử, E - Mô-đun đàn hồi,  ` ` - Khoảng cách từ đầu bên trái phần tử dầm đến vết nứt.

Xem rằng khối lượng mất đi do vết nứt là bé so với khối lượng chung của phần tử, nên ma trận khối lượng của phần tử có vết nứt cũng được tính như ma trận khối lượng phần tử dầm thông thường:

 

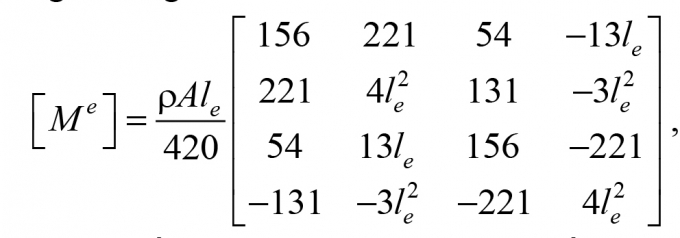 (9)

 

với  P - Khối lượng riêng của vật liệu dầm; A - Diện tích mặt cắt ngang của phần tử.

3.2. Phần tử dầm trên nền đàn hồi

Phần tử dầm trên nền đàn hồi được mô hình hóa như dầm có liên kết với các phần tử đàn hồi và theo các phương dọc trục và vuông góc với trục dầm (Hình 3.2).

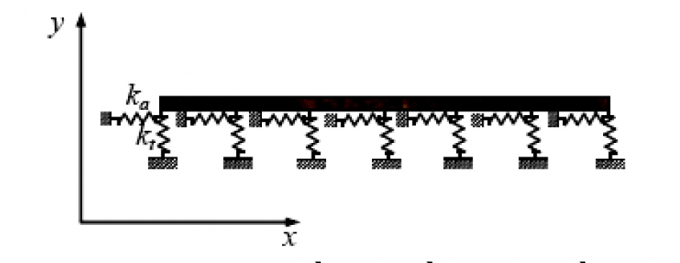Hình 3.2: Mô hình phần tử dầm trên nền đàn hồi

 

Ma trận độ cứng phần tử dầm trên nền đàn hồi [K_bf ^e]  =  [K_b ^e] + [Kf ^e] (10)

được xác định bởi [3], [7]:

Trong đó: [K_b ^e] = [K^e ] - Ứng với phần tử dầm không có vết nứt; [K_b ^e] = [K_c^e]  - Ứng với phần tử dầm có vết nứt;  [K]- Ma trận độ cứng liên quan đến nền đàn hồi, xác định bởi [3].

3.3. Phương trình mô tả dao động của phần tử dầm có vết nứt trên nền đàn hồi chịu khối lượng di động

Sử dụng nguyên lý Hamilton [8]:

 

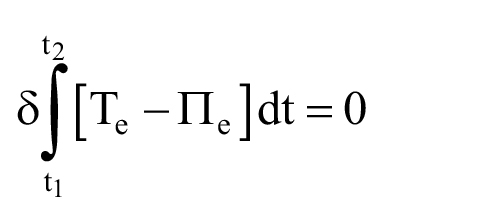(11)

 

 

 

Trong đó: T_e - Động năng và P_e thế năng của phần tử.

Dẫn đến phương trình vi phân mô tả dao động của phần tử dầm có vết nứt đặt trên nền đàn hồi chịu tác dụng của khối lượng di động:

 

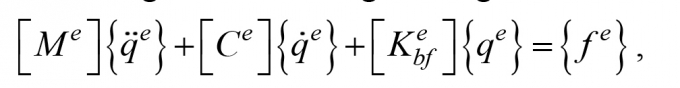(12)

 

với {f^e}- Véc-tơ tải trọng nút của phần tử do khối lượng di động tác dụng.

Theo phương pháp PTHH, khi có tải trọng di động tham gia vào sự làm việc của hệ, do tính chất thay đổi vị trí của tải trọng theo thời gian, nên tại mỗi thời điểm, tải trọng di động tác dụng lên một phần tử dầm.

Xét phần tử dầm chịu tác dụng của khối lượng m di động, trên m có lực P(t) tác dụng (Hình 3.3).

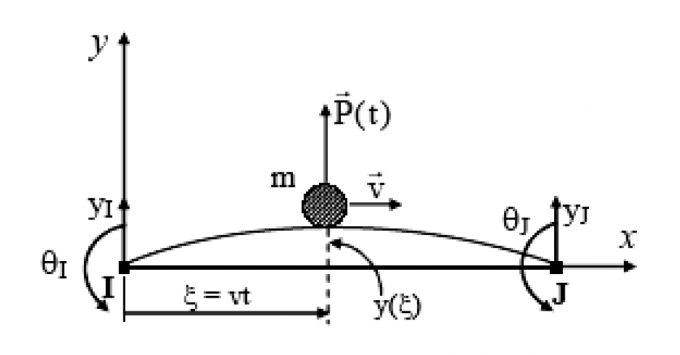Hình 3.3: Phần tử dầm chịu tác dụng của hệ khối lượng di động và lực

 

Lực tác dụng của tải trọng di động lên dầm tại tọa độ x =`xi` = vt là [7]:

 

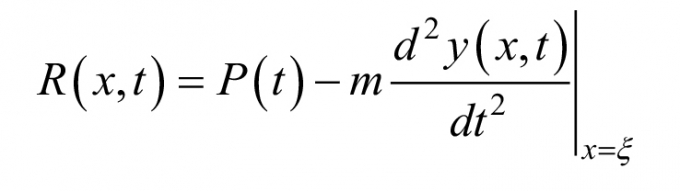(13)

 

 

với y(x,t) - Độ võng phần tử;  d²y / dt² - Gia tốc tuyệt đối của khối lượng di động theo phương y.

Sau khi lấy đạo hàm của hàm độ võng, biểu thức (13) được viết lại:

 (14)

 

(15)

 

(16)

 

(17)

(18)

 

(19)

(20)

(21)

(22)

(23)

 

Với biểu thức (19), ta có phương trình mô tả dao động của phần tử dầm có vết nứt đặt trên nền đàn hồi, chịu tác dụng của khối lượng di động:

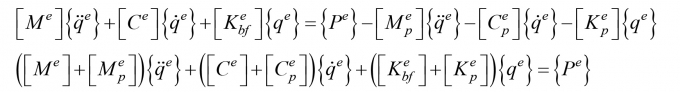 (24)

 

 

4. PHƯƠNG TRÌNH MÔ TẢ DAO ĐỘNG CỦA DẦM CÓ VẾT NỨT NẰM TRÊN NỀN ĐÀN HỒI CHỊU TÁC DỤNG CỦA KHỐI LƯỢNG DI ĐỘNG VÀ PHƯƠNG PHÁP GIẢI

Từ phương trình (24), sau khi ghép nối các ma trận, véc-tơ tải trọng phần tử thành các ma trận, véc-tơ tải trọng tổng thể, ta có phương trình mô tả dao động của dầm có vết nứt đặt trên nền đàn hồi chịu tác dụng của khối lượng di động và lực P(t) [7], [8]:

 (25)

 

Trong đó: 

    e_m - Số phần tử chịu trực tiếp khối lượng di động; a_R, b_R - Các hằng số cản Rayleigh.

Các tác giả sử dụng phương pháp tích phân trực tiếp Newmark để giải phương trình (25), tại mỗi thời điểm tính tích phân, xác định vị trí tải trọng di động và cập nhật các ma trận bổ sung [M_p^e], [C_p ^e], [K_p ^e]  của phần tử vào ma trận tổng thể của hệ.

Chương trình tính có tên Crakedbeam_ Foundation_Massmoving (CBFM) được xây dựng trong môi trường Matlab.

Kiểm tra độ tin cậy của chương trình đã lập, tác giả giải bài toán dầm có vết nứt với các số liệu xuất phát như trong công trình của Murat Reis và Yasar Pala [4].

Số liệu tính: Dầm dài L = 8m, một đầu liên kết ngàm, một đầu tự do, vật liệu có mô-đun đàn hồi E = 2,06.10¹¹ N/m², hệ số Poisson n = 0,3, khối lượng riêng r =7.800 kg/m³. Mặt cắt ngang hình chữ nhật bxh = 0,1mx0,2m. Chính giữa dầm có vết nứt hở chữ V, độ sâu vết nứt d = 0,1 m. Vật có khối lượng m = 1.000kg chuyển động dọc dầm với vận tốc v = 10m/s.

Bảng 4.1. Kết quả so sánh kiểm tra độ tin cậy của chương trình

Với sai số 4,32% như trên, có thể khẳng định chương trình CBFM đã lập là có cơ sở tin cậy.

5. KHẢO SÁT SỐ

Số liệu dầm: Dầm có chiều dài L=8m, mặt cắt ngang hình chữ nhật bề rộng b = 0,1m, chiều cao h = 0,2m; một đầu liên kết gối cố định, một đầu liên kết gối di động. Vật liệu dầm có mô-đun đàn hồi E = 2,1.10¹¹ N/m², hệ số Poisson  khối lượng riêng  p= 7,8.10³ kg/m³. Chính giữa dầm có vết nứt hở dạng chữ V, độ sâu vết nứt d = 0,1m.

Nền đàn hồi có độ cứng lò xo theo phương pháp tuyến và tiếp tuyến lần lượt là k_t = 2.10⁴N/m, k_a = 1.10⁴N/m. Tải trọng sử dụng là chất điểm có khối lượng m = 1.000kg, di chuyển dọc dầm (từ đầu liên kết gối cố định đến đầu liên kết gối di động) với vận tốc v = 36km/h.

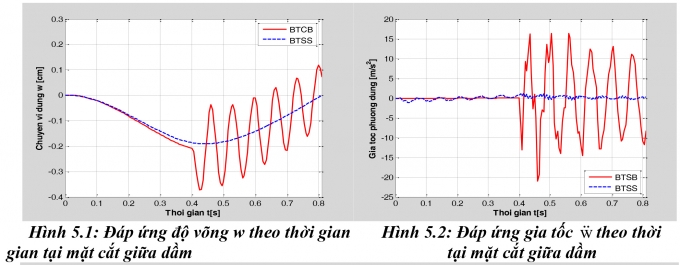
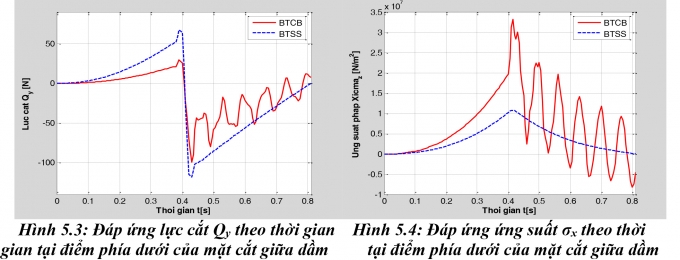
Với chương trình tính đã lập, tác giả tính toán cho 02 trường hợp: Dầm có vết nứt (bài toán cơ bản - BTCB) và không có vết nứt (bài toán so sánh - BTSS) để thấy rõ hơn sự ảnh hưởng đến đáp ứng động của hệ khi vết nứt xuất hiện. Kết quả đáp ứng độ võng w, gia tốc , lực cắt Q_y và ứng suất pháp tại điểm giữa dầm (điểm A(0,0,4)) được thể hiện như Bảng 5.1 và Hình 5.1, 5.2, 5.3, 5.4.

 

 

Bảng 5.1. Tóm tắt giá trị lớn nhất các đại lượng tính

 

5.1. Ảnh hưởng của độ cứng nền đàn hồi

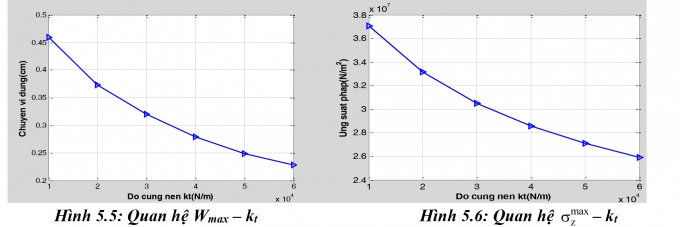
Nghiên cứu sự thay đổi các giá trị lớn nhất của chuyển vị, nội lực, ứng suất pháp của dầm theo độ cứng nền đàn hồi, thông qua độ cứng k_t của lò xo biến thiên từ 1.10⁴N/m đến 6.10⁴N/m. Kết quả sự thay đổi giá trị chuyển vị, gia tốc, lực cắt và ứng suất pháp lớn nhất tại mặt cắt giữa dầm được thể hiện như trên Bảng 5.2 và các đồ thị Hình 5.5 và 5.6.

Bảng 5.2. Tóm tắt giá trị lớn nhất các đại lượng tính theo k_t

 

Nhận xét: Khi độ cứng nền tăng thì giá trị chuyển vị, mô-men uốn lớn nhất giảm do độ cứng tổng thể của hệ tăng. Giá trị chuyển vị, mô-men uốn lớn nhất giảm mạnh khi k_t biến thiên từ 1.10⁴N/m đến 3.10⁴N/m, sau đó tốc độ giảm nhỏ hơn.

5.2. Ảnh hưởng của tốc độ tải trọng

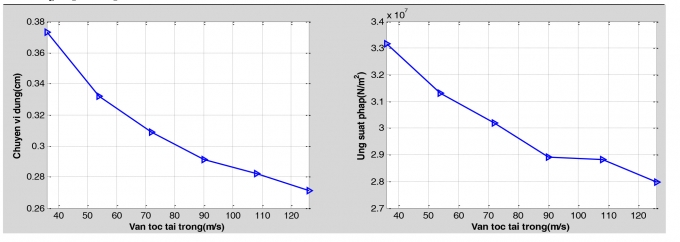
Khảo sát bài toán với tốc độ tải trọng v thay đổi từ 10m/s (36km/h) đến 35m/s (126km/h). Kết quả sự biến thiên các giá trị lớn nhất về độ võng, gia tốc, lực cắt và ứng suất tại điểm giữa dầm theo v thể hiện như Bảng 5.3 và các đồ thị Hình 5.7 và 5.8.

Bảng 5.3. Tóm tắt giá trị lớn nhất các đại lượng tính theo v

 

Hình 5.7: Quan hệ Wmax - v                                         Hình 5.8 : Quan hệ `Sigma`  zmax   -v

Nhận xét: Khi vận tốc di chuyển của tải trọng tăng thì chuyển vị, nội lực và ứng suất lớn nhất trong dầm giảm, khi vận tốc di chuyển của tải trọng thay đổi từ 90m/s đến 110m/s thì ứng suất pháp không thay đổi nhiều, sau đó lại giảm mạnh.

5.3. Ảnh hưởng của vị trí vết nứt

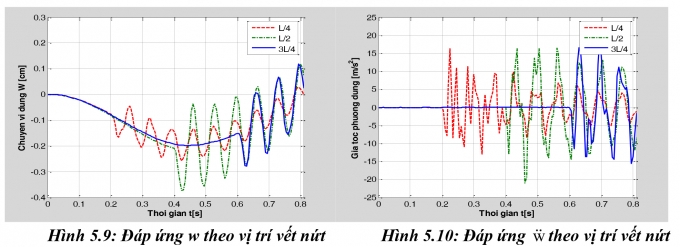
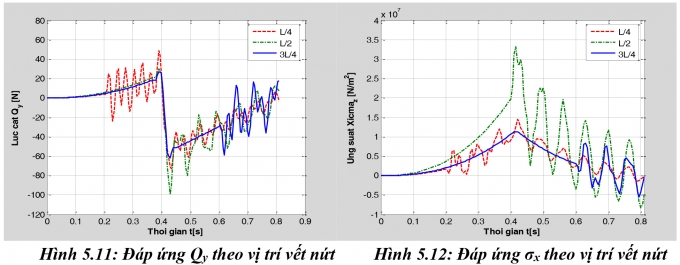
Nghiên cứu sự thay đổi các giá trị lớn nhất của chuyển vị, nội lực của dầm theo vị trí vết nứt, cho vết nứt tại các vị trí cách đầu dầm bên trái các khoảng L/4, L/2, 3L/4. Kết quả giá trị cực trị của đáp ứng tại điểm tính được thể hiện như trên Bảng 5.4 và các đồ thị như Hình 5.9, 5.10, 5.11 và 5.12.

 

 

Bảng 5.4. Tóm tắt giá trị lớn nhất các đại lượng tínhtheo vị trí vết nứt

 

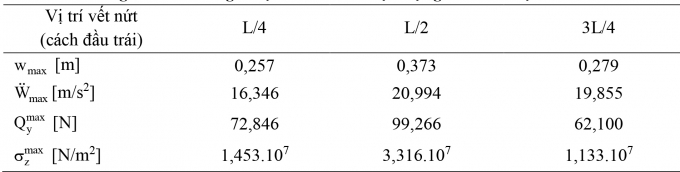Nhận xét: Vị trí vết nứt thay đổi thì đáp ứng chuyển vị, ứng suất và nội lực lớn nhất trong dầm có sự thay đổi rõ rệt, khi vết nứt ở chính giữa dầm các đại lượng trên đạt giá trị lớn nhất, như vậy, dầm nguy hiểm nhất khi xuất hiện vết nứt ở vị trí này.

6. THẢO LUẬN VÀ KẾT QUẢ

Nội dung chính của bài báo:

- Xây dựng thuật toán, chương trình giải hệ phương trình vi phân có hệ số phụ thuộc thời gian mô tả dao động của dầm có vết nứt trên nền đàn hồi trên cơ sở phương pháp tích phân trực tiếp Newmark.

- Khảo sát số xác định phản ứng động của hệ dưới tác dụng của khối lượng di động, kết quả cho phép khảo sát bài toán với nhiều thông số thay đổi để lựa chọn các thông số hợp lý cho hệ theo các tiêu chí như độ bền, độ ổn định.

Tài liệu tham khảo

[1]. Salih N Akour1 (2010), Dynamics of Nonlinear Beam on Elastic Foundation, Proceedings of the World Congress on Engineering 2010 Vol II WCE 2010, June 30 - July 2, 2010, London, U.K., ISBN: 978-988-18210-7-2 ISSN: 2078-0958 (Print); ISSN: 2078-0966 (Online).

[2]. S. T. Oni and T. O. Awodola (2010), Dynamic response under a moving load of an elastically sup-ported non-prismatic Bernoulli-Euler beam on variable elastic foundation, Latin American Journal of Solids and Structures, 7(2010) 3 - 20.

[3]. Karmvir, Ramakrishna Kuppa (2014), Overview of methods of analysis of beams on elastic foundation, IOSR Journal of Mechanical and Civil Engineering, Volume 11, Issue5.Ver VI (Sep Oct), pp. 22-29.

[4]. Murat .R and Yasar. P (2012), Vibration of a Cracked Cantilever Beam under Moving Mass Load, Journal Of Civil Engineering and Management, ISSN 1822-3065 online, Vol 18 (1) pp.106-113.

[5]. Animesh C. and Tanuja S. V. (2015), Dynamic Analysis of Beam under the moving Mass for Damage Assessment, International Journal of Engineering Research & Technology, ISSN: 2278-0181, Vol. 4 Issue 02, February, pp.788-796.

[6]. M. Attar et al (2015), Dynamic response of cracked Timoshenko beams on elastic foundation under moving harmonic loads, Journal of Vibration and Control. DOI: 10.1177/1077546315580470. pp 1-26.

[7]. Nguyễn Thái Chung, Nguyễn Trang Minh và Lê Phạm Bình (2015), Phân tích động lực học của dầm có vết nứt chịu tác dụng của tải trọng di động bằng phương pháp phần tử hữu hạn, Tuyển tập công trình Hội nghi Cơ học vật rắn biến dạng toàn quốc lần thứ 12, trang 223 - 230. Đà Nẵng.

[8]. Bathe K. J. and Wilson E. L. (1978), Numerical Method in Finite Method Analyis, Prentice Hall of India Private Limited, New Delhi.