Phát triển phương pháp cân bằng giới hạn tổng quát trong tính toán ổn định bờ dốc

ThS. Trần Trung Dũng Trường Đại học Giao thông vận tải Người phản biện: TS. Nguyễn Viết Thanh TS. Nguyễn Trung Kiên

Tóm tắt: Phương pháp cân bằng giới hạn tổng quát (Generalized Limit Equilibrum Method - GLEM) đã được Enoki giới thiệu năm 1990 để tính toán ổn định bờ dốc. Điểm nổi bật của phương pháp này so với phương pháp cân bằng giới hạn khác là lăng thể trượt được coi là hệ thống các khối trượt con, ở đó mặt đáy và mặt bên của khối trượt con chính là mặt trượt. Trong khi đó, với các phương pháp cân bằng giới hạn thông thường, lăng thể trượt được chia thành các mảnh, ở đó chỉ có mặt đáy của các mảnh là mặt trượt còn mặt bên là các mặt thẳng đứng và điều kiện trượt không thỏa mãn trên đó. Trong bài báo, các tác giả nghiên cứu và phát triển phương pháp (GLEM) để tính toán ổn định bờ dốc dưới tác dụng của tải trọng tĩnh.

Từ khóa: Cân bằng giới hạn tổng quát, ổn định bờ dốc, tải trọng tĩnh.

Abstract: Generalized Limit Equilibrium Method - GLEM was introduced by Enoki in 1990 to analyze the stability of earth slopes. The advantage point of this method is that the the sliding soil mass is considered as a lock system, of which the bottom planes and inter-block planes are just the slip planes, whereas in ordinary Limit Equilibrium Methods (LEM), the sliding soil mass is considered as the pieces, of which only the bottom planes are the slip planes, the inter-piece planes are vertical and on these planes the slip condition is not satisfied. In this paper, the authors would you like to develop the GLEM to analyze stability of earth slopes.

Keywords: Generalized limit equilibrum method, earth slopes stability, stability.

1. Đặt vấn đề

Trong phương pháp cân bằng giới hạn thường giả định các mặt trượt là mặt phẳng hoặc mặt trượt trụ tròn. Lăng thể trượt được coi là một cố thể, điều kiện trượt chỉ xảy ra tại mặt đáy của lăng thể trượt, khi tính toán lăng thể trượt có thể được chia thành các mảnh chia nhỏ với mặt giữa các mảnh là thẳng đứng và không xảy ra điều kiện trượt trên các mặt phẳng này [1], [2].

Nhưng theo lời giải của Sokolovsky [3] thì khi mái đất đặt tới trạng thái cân bằng giới hạn thì trong lăng thể trượt xuất hiện hai họ đường trượt xiên góc với nhau. Như vậy, nếu quan điểm theo các phương pháp cân bằng giới hạn thông thường thì ta mới chỉ xét được một họ đường trượt mà thôi. Để khắc phục hạn chế này, tác giả đã phát triển phương pháp cân bằng giới hạn tổng quát (GLEM) để giải quyết bài toán ổn định mái dốc [4]. Phương pháp này là ta chia lăng thể trượt thành các khối con và điều kiện trượt không những xảy ra trên mặt đáy mà còn xảy trên cả mặt giữa của các khối con, tức là cả hai họ đường trượt được xét đến. Do mặt trượt chính là mặt đáy của các khối con nên không nhất thiết mặt trượt tổng quát của lăng thể trượt là mặt trượt trụ tròn hay mặt phẳng. Vì vậy, phương pháp (GLEM) cho thấy cũng có ưu điểm nhất định so với các phương pháp cân bằng giới hạn thông thường.

2. Giới thiệu phương pháp GLEM

2.1. Giả thiết

Đất được coi là đồng nhất có ứng xử cứng dẻo lý tưởng, trong bài toán này không xét tới mực nước ngầm và biến đổi thể tích của đất.

2.2. Sơ đồ tính mái dốc trong GLEM

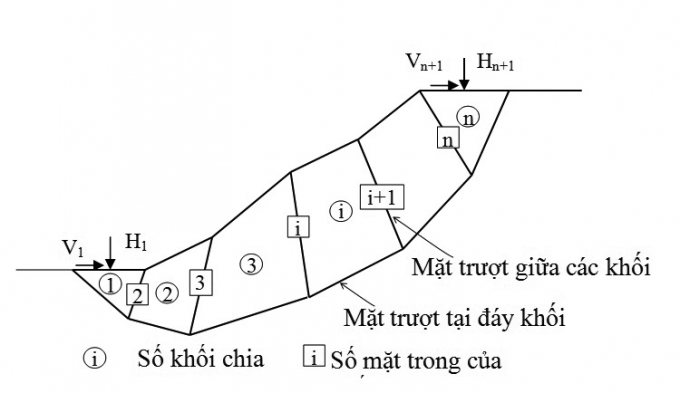Hình 2.1: Sơ đồ các khối trượt trong phương pháp GLEM

Lăng thể trượt được chia thành các khối dạng tam giác và tứ giác, các khối được giới hạn bởi mặt đáy, mặt trong và khi mái đất bị mất ổn định trạng thái cân bằng giới hạn có thể xảy ra trên cả mặt phẳng đáy và mặt trong của khối. Chỉ điều kiện cân bằng lực được sử dụng, không cần sử dụng điều kiện cân bằng mô men.

3. Phát triển GLEM tính ổn định mái dốc

3.1. Mô hình tính ổn định mái đất bằng phương pháp cân bằng giới hạn tổng quát

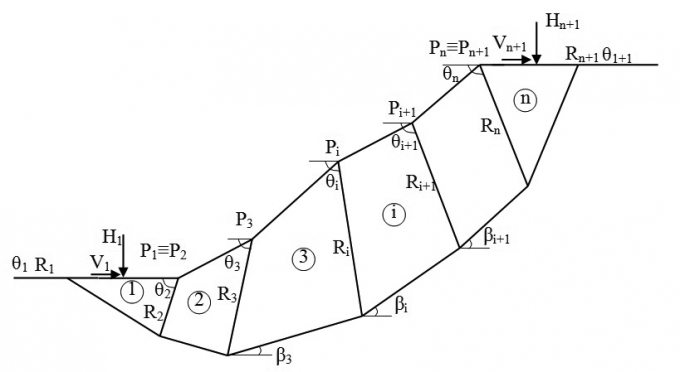Hình 3.1: Mô hình tính ổn định mái dốc

3.2. Các phương trình cơ bản

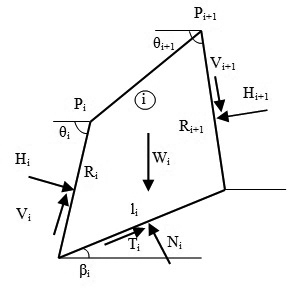Hình 3.2: Các lực tác dụng lên khối

 

Xét điều kiện cân bằng của khối: Chiếu các lực tác dụng lên khối theo phương pháp tuyến của mặt đáy ta có:

 

(1)

Chiếu các lực tác dụng lên khối theo phương tiếp tuyến của mặt đáy ta có:                

 

(2)

 

 

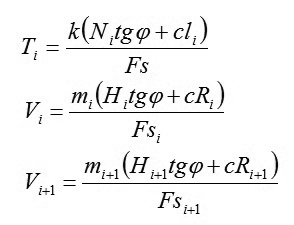(3)

 

(4)

 

 

 

3.3. So sánh số phương trình và số ẩn                                                                              

Dựa vào các hệ phương trình (1), (2), (3), (4) ta có:

Bảng 3.1. Tổng hợp số phương trình và số ẩn của n khối chia

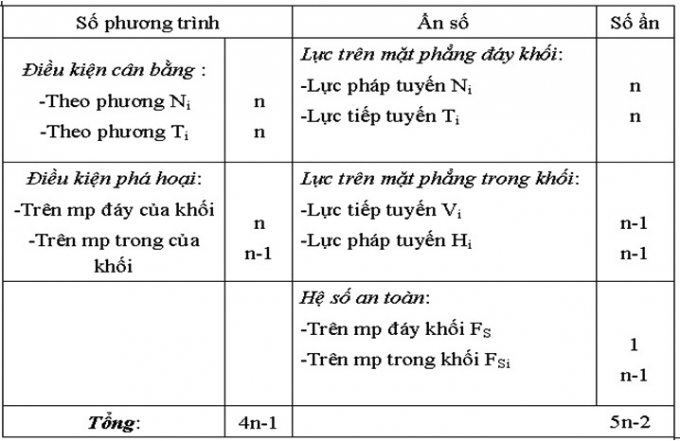Từ bảng tổng hợp trên ta thấy, số phương trình ít hơn số ẩn, do đó để giải quyết bài toán này ta có thể có hai hướng giải quyết như sau:

Trường hợp 1: Coi lăng thể trượt là vật thể nguyên khối, điều đó có nghĩa hệ số an toàn trên mặt trong giữa các khối Fsi = ∞, như vậy số ẩn bằng số phương trình 4n-1 và ta luôn giải được bài toán này để xác định Fs_min.

Trường hợp 2: Khi mái đất đạt tới trạng thái cân bằng giới hạn thì mặt trượt không những chỉ xảy ra trên mặt đáy mà còn xảy ra trên cả mặt trong giữa các khối (xét cả hai họ đường trượt), có nghĩa Fs= Fs_i, như vậy số ẩn bằng số phương trình 4n-1, giải bài toán ta đi xác định Fsmed.

3.4. Xây dựng thuật toán tối ưu hóa tìm mặt trượt nguy hiểm

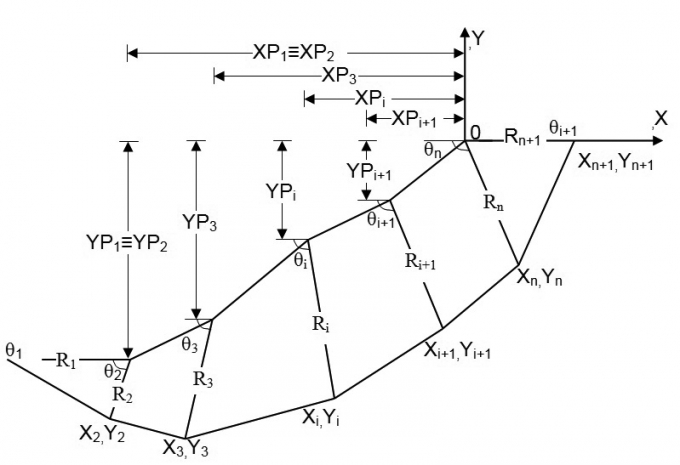Hình 3.3: Các quy ước ký hiệu hình học các khối trượt

 Hàm mục tiêu là hệ số an toàn Fs_min

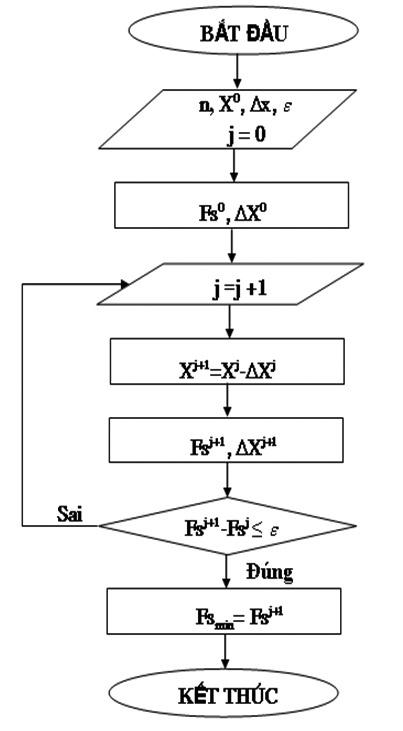
3.5. Sử dụng phương pháp lặp Newton tìm cực trị Fs_min

Sơ đồ khối tìm Fs_min

 

4. Ví dụ tính toán và so sánh kết quả tính của một số các tác giả

Tính ổn định mái đất dính đồng nhất bằng phương pháp GLEM và so sánh kết quả với các phương pháp khác

Bảng 4.1. Kết quả tổng hợp

Kết quả chỉ ra rằng, hệ số an toàn tính theo phương pháp của Fellenius cho kết quả nằm trong khoảng giá trị Fs_min và Fs_med mà tác giả tính theo GLEM, còn theo Bishop kết quả lớn hơn Fs_med một chút.

Ta cũng nhận thấy rằng, hệ số an toàn mặt đáy Fs_min theo GLEM là giá trị bé nhất trong tất cả các phương pháp tính nêu trên, chứng tỏ phương pháp GLEM mà tác giả tính đã đánh giá được mái dốc làm việc ở trạng thái bất lợi nhất.

5. Kết luận

Đã nghiên cứu và phát triển cơ sở lý thuyết của phương pháp cân bằng giới hạn tổng quát của Enoki và các cộng sự, xây dựng thuật toán và chương trình tính ổn định mái đất trên máy tính cho trường hợp mái đất đồng nhất.

Tài liệu tham khảo

[1]. Fellenius, W. (1936), Calculation of  the stability of earth dams - Proc, the 2nd Congress on Large Dams,445-462.

[2]. Bishop, A.W. (1945), The use of slip circle in stability analysis of slop stability- Geotechnique.

[3]. Sokolovsky, V.V. (1960), Static of soil media - London, Butterworth^’s Scientific Publications.

[4]. Enoki, N.Yagi, R.Ytabe, E. Ichimoto (1990), Generalized slice method for slope stability analysis, Soil and Foundations - Japanese Soc, Of Soi Mech.