Liên hệ quảng cáo
Sử dụng nguyên lý DAlembert để thành lập phương trình dao động của đường ray đường sắt
Hiện nay, khi xây dựng các tuyến đường sắt trong đô thị, chúng ta cần phải giải quyết nhiều bài toán phức tạp có liên quan đến ảnh hưởng rung động của chuyển động đoàn tàu, trong đó có bài toán nghiên cứu lực động từ đoàn tàu tác dụng lên đường và công trình nhân tạo
|
TS. Lê Công Thành ThS. NCS. Nguyễn Bình Trường Đại học Giao thông vận tải Người phản biện: TS. Trần Quốc Đạt ThS. Nguyễn Văn Chinh |
Tóm tắt: Hiện nay, khi xây dựng các tuyến đường sắt trong đô thị, chúng ta cần phải giải quyết nhiều bài toán phức tạp có liên quan đến ảnh hưởng rung động của chuyển động đoàn tàu, trong đó có bài toán nghiên cứu lực động từ đoàn tàu tác dụng lên đường và công trình nhân tạo. Để làm sáng tỏ và hoàn thiện các mô hình tính toán lực động của đoàn tàu, bài báo đề xuất sử dụng nguyên lý D’Alembert để xây dựng phương trình dao động làm cơ sở đánh giá ảnh hưởng của lực động của đoàn tàu lên kết cấu của đường sắt, qua đó có giải pháp chống rung để hạn chế ảnh hưởng tác động do rung động cộng hưởng gây nên.
Từ khóa: Phương trình dao động đường ray, nguyên lý D’Alembert, động lực học đoàn tàu.
Abstract: Currently, the construction of railway lines in urban areas, we need to solve more complex problems related to vibrations affect train movement, including its research problem from union ship effect on sugar and artificial works. To clarify and complete the calculation model of fleet capacity, the paper proposed using D’ Alembert principle to build oscillation equation as the basis of its assessment of the impact on train structure of rail, which have anti-vibration solutions to limit the impact by affecting resonant vibration triggers.
Keywords: Oscillating rails equation, D’Alembert principle, train dynamics.
1. Nội dung
1.1. Nguyên lý D’Alembert
Trong tính toán động lực học của đoàn tàu lên đường ray, để thành lập các phương trình chuyển động có thể sử dụng nguyên lý D’Alembert. Theo nguyên lý D’Alembert, phương trình chuyển động có thể đưa về dạng phương trình cân bằng lực nếu như gắn thêm lực quán tính vào các vật thể chuyển động.
Giả sử ta có chất điểm chuyển động dưới tác dụng của lực chủ động `barF` a và phản lực `barN`. Tổng hợp lực chuyển động sẽ được xác định như sau:
`barR` = `barN` + `barF` a ( 1)
Khi đó:
`barR` + `barF` qt = 0
Trong đó: `barF` = - m`bara` - Lực quán tính (dấu “ - ” thể hiện lực quán tính ngược hướng so với gia tốc a).
Nguyên lý D’Alembert được phát biểu như sau: “Nếu như đặt thêm một lực quán tính vào vật thể chịu tác động của lực chủ động và các phản lực thì vật thể đó sẽ ở trạng thái cân bằng (nghĩa là tổng tác động của các lực chủ động, lực phản lực và hợp lực của các lực quán tính bằng không)”.
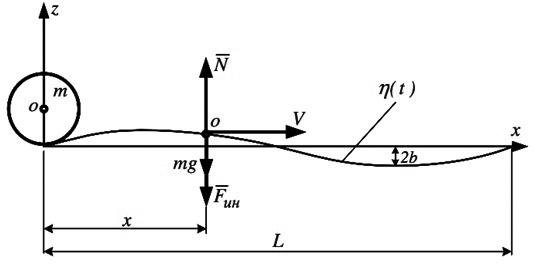 |
| Hình 1.1: Chuyển động của bánh xe trên đường không bằng phẳng |
2b - Chiều cao vị trí lồi lõm; x - Tọa độ điểm khảo sát; V - Vận tốc chuyển động; M - Khối lượng bánh xe; L - Chiều dài đoạn lồi lõm
1.2. Sử dụng nguyên lý D’Alembert để lập phương trình dao động của đoàn tàu trên đường không bằng phẳng
Để đơn giản tính toán, ta thực hiện khảo sát chuyển động của một bánh tàu khối lượng m trên đường cứng tuyệt đối. Sơ đồ tính toán đưa ra trong Hình 1.1. Có thể nhận thấy rằng, đại đa số các biến dạng của đường ray có dạng hình sin. Giả thiết rằng các công thức toán học sơ cấp có thể mô tả tương đối đúng hình dạng của các biến dạng theo phương trình sau đây:
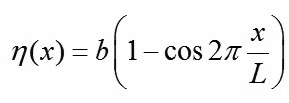 |
(3)
Lấy ký hiệu vận tốc tịnh tiến của bánh xe là V, khi đó tại thời điểm khảo sát, so với điểm đầu đoạn biến dạng, bánh xe vượt qua quãng đường: X = Vt. Khi đó công thức (3) có thể đưa về dạng:
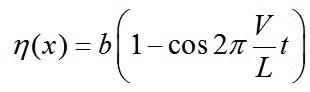 |
(4)
Giả thiết rằng đường cứng tuyệt đối nên sẽ không có biến dạng khi bánh xe đi qua. Do đó, chuyển dịch thẳng đứng của bánh xe Zk sẽ bằng mức độ lồi lõm của biến dạng: Zk = η (x)
Vận tốc theo phương z của bánh xe sẽ là đạo hàm của dịch chuyển thẳng đứng:
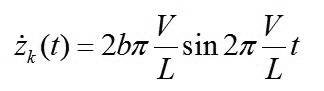 |
(5)
Gia tốc theo phương z của bánh xe sẽ là đạo hàm bậc hai của dịch chuyển thẳng đứng:
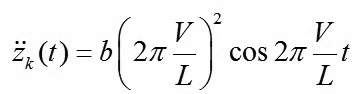 |
(6)
Lực quán tính của bánh xe xác định theo công thức:
(7)
Sử dụng nguyên lý D’Alembert, viết phương trình cân bằng cho trường hợp chuyển động của bánh xe:
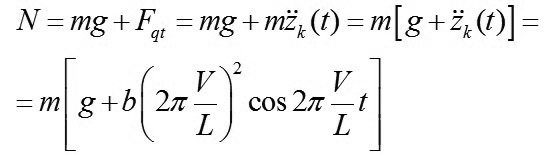 |
(8)
Như vậy, tác động của bánh tàu lên ray sẽ phụ thuộc vào khối lượng của bánh xe chủ động, vào hình thái và quy luật biến đổi của biến dạng, cụ thể là vào các giá trị L, b và vận tốc chuyển động V.
1.3. Thành lập phương trình dao động của đường ray theo phương thẳng đứng
Để phân tích các đặc trưng động học của đường ray đường sắt có thể đưa ra sơ đồ tính toán như Hình 1.2. Sơ đồ này gần với sơ đồ làm việc của các phương tiện có giá treo gắn trên lò xo đơn. Khối lương m tương ứng với tổng khối lượng của thân xe và khung gầm, độ cứng ψ và hệ số tắt dần dao động â thể hiện đặc tính của hệ lò xo.
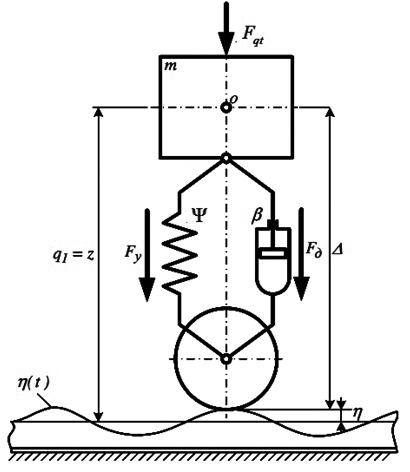 |
| Hình 1.2: Mô hình phẳng có một bậc tự do dưới tác động của kích thích bên ngoài |
ψ - Độ cứng của liên kết đàn hồi;
β- Hệ số tiêu tán (tắt dần dao động);
η - Biên độ dao động;
m - Khối lượng tính cho một bánh;
z - Dịch chuyển tuyệt đối;
∆ - Dịch chuyển tương đối (độ võng)
Khi hệ chuyển động các lực kích thích sẽ gây ra dao động theo phương thẳng đứng đối với khối lượng phía trên giá treo của phương tiện, đặc trưng bởi tọa độ q1=z. Hệ sẽ chịu tác động của các lực:
Lực quán tính:
(9)
Lực đàn hồi:
(10)
Lực tiêu tán:
(11)
Sử dụng nguyên lý D’Alembert có thể viết phương trình dao động của hệ về dạng:
(12)
Hay:
(13)
Sau khi biến đổi công thức (13) ta có:
(14)
Phương trình (14) cho ta thấy dạng phương trình dao động theo phương thẳng đứng với một bậc tự do. Phía bên trái là thành phần dao động riêng, phía bên phải là dao động cưỡng bức từ lực xung kích xuất hiện khi đường bị biến dạng. Giải phương trình nêu trên cho ta các giá trị dịch chuyển z, vận tốc ż và gia tốc cũng như đánh giá một cách tương đối đặc điểm động lực học của đường.
1.4. Giải phương trình dao động theo phương thẳng đứng
Để giải phương trình dao động theo phương thẳng đứng theo công thức (14) có thể sử dụng phần mềm Midas. Các số liệu tính toán ban đầu: Khối lượng m=6,5T; độ cứng của liên kết đàn hồi ψ=1500kN/m; hệ số tiêu tán β = 40kNs/m; phát sinh lực xung kích do đường gồ ghề dạng hình sin có chiều dài L = 2m, chiều cao b = 0,005m; vận tốc chuyển động của đoàn tàu Vtb = 11,1m/s (40km/h); Vmax=22,2m/s (80 km/h).
Dưới đây là trình tự lập trình với dòng giải thích (GT) và dòng lệnh (>):
GT: Bắt đầu chương trình;
> restart;
GT: Nhập các tham số của mô hình (khối lượng, độ cứng, hệ số phân tán) và vận tốc chuyển động;
> m: = 6.5; G: = 1500; beta: = 40; v = 10;
GT: Nhập các thông số của đoạn gồ ghề biến dạng;
> L: = 2; b: = 0,005;
GT: Nhập phương trình đoạn gồ ghề biến dạng (công thức 4);
> n(t): = b*(1+cos(2*Pi*V*t/L));
GT: Nhập phương trình dao động (công thức 14);
> du: = m*diff(z(t), t$2) + beta*diff(z(t),t) + G*z(t) = beta*diff(n(t),t) + G*n(t);
GT: Giải phương trình vi phân với các giá trị ban đầu bằng bằng không;
> res: = dsolve({du,z(0) = 0, D(z) (0) = 0}, z(t));
GT: Xuất kết quả;
> assign(res): z: = z(t);
GT: Xây dựng đồ thị và dạng đoạn đường biến dạng trong khoảng thời gian từ 0 đến 2s;
> plot([z, n(t)], t = 0…2, colour = [blue, black]);
GT: Xây dựng đồ thị vận tốc theo phương đứng, gia tốc trong khoảng thời gian từ 0 đến 2s;
>plot([diff(z, t)*10, diff(z,t$2)],t=0…2, colour=[green, gold]);
Từ đồ thị (Hình 1.3, 1.4) có thể thấy rằng dao động riêng của hệ khi có lắp thiết bị chống rung sẽ tắt rất nhanh, và trong một hệ đang chịu tác động của dao động cưỡng bức sinh ra do đường không bằng phẳng với tần số dao động cưỡng bức.
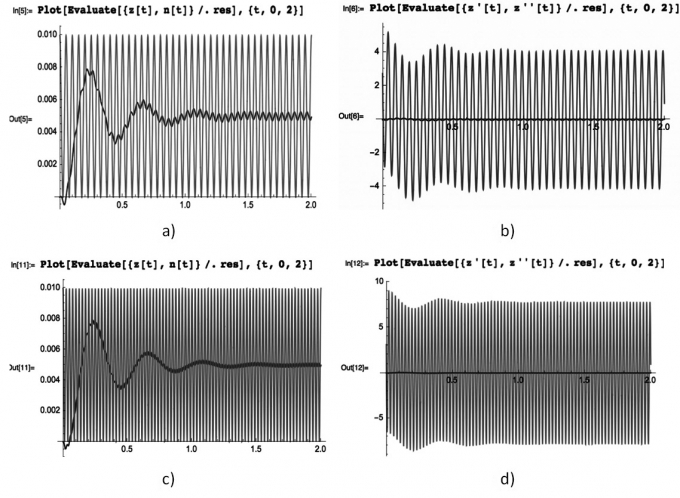 |
| Hình 13 |
Thiết bị chống rung sẽ giúp cho hệ chống lại hiện tượng cộng hưởng.
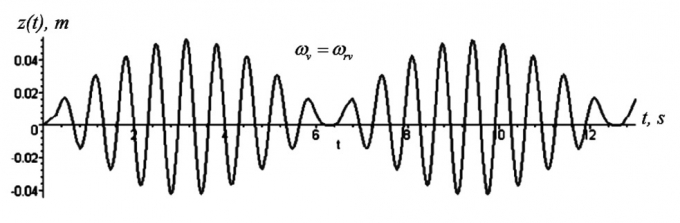 |
| Hình 1.4: Đồ thị dao động khi ωv=ωrv |
Nghiên cứu lý thuyết hiện tượng dao động khi không có thiết bị chống rung (β = 0), cộng hưởng sẽ xuất hiện khi tần số dao động của lực cưỡng bức ωv trùng với tần số dao động riêng .
Xem xét trường hợp khi giá trị của ωv tiến gần tới giá trị của ωrv = `sqrt( psi/m)` (Hình 1.5), biên độ dao động sẽ tăng giảm theo chu kỳ do tồn tại cùng lúc hai dao động điều hòa có cùng biên độ nhưng khác về tần số. Sự khác biệt về pha không ngừng thay đổi và có thời điểm chúng hoàn toàn hòa nhập với nhau.
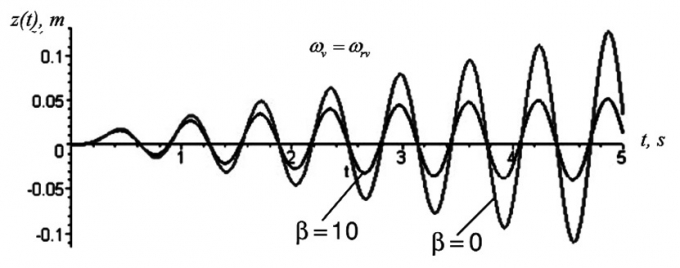 |
| Hình 1.5: Đồ thị dao động khi có cộng hưởng trong trường hợp không có thiết bị chống rung β = 0 và có thiết bị chống rung β = 10 |
Nếu ωv=ωrv trong hệ thống sẽ xảy ra công hưởng. Trong Hình 1.5, biên độ dao động khi không có thiết bị chống rung (β = 0) sẽ tăng dần theo thời gian. Điều này dẫn đến lực động tác dụng lên đường sẽ tăng đáng kể và gây phá hoại kết cấu đường. Khi có bộ phận giảm chấn, đầu tiên biên độ sẽ tăng, sau đó không thay đổi. Hiện tượng cộng hưởng bị dập tắt bởi thiết bị chống rung. Từ phương trình dao động nêu trên thể thay đổi các thông số đầu vào và thực hiện phân tích cho các trường hợp khác nhau.
2. Kết luận
- Nghiên cứu chỉ ra rằng có thể sử dụng nguyên lý D’Alembert để xây dựng phương trình dao động của đoàn tàu cũng như của đường ray theo phương thẳng đứng. Theo nguyên lý này, hợp lực của các lực chủ động và các liên kết sẽ cân bằng với lực quán tính đặt lên hệ.
- Với mô hình tính toán đơn giản đưa ra trong bài báo đã có thể phần nào giải thích cơ chế hình thành lực động, hiện tượng cộng hưởng và sự cần thiết phải hoàn thiện các thiết bị chống rung trên đường sắt.
Tài liệu tham khảo
[1]. Nguyễn Hữu Dũng (2006), Động lực học đầu máy diezel, Trường Đại học GTVT.
[2]. Phạm Văn Ký, Cơ sở động lực học đường sắt, Bài giảng Bộ môn Đường sắt - Trường Đại học GTVT.
[3]. Nguyễn Thanh Tùng (2007), Kết cấu tầng trên đường sắt, NXB. GTVT.
Tag:






Bình luận
Thông báo
Bạn đã gửi thành công.