Khảo sát đặc điểm ổn định của mô hình trạng thái gián đoạn của máy điện không đồng bộ rotor dây quấn

ª TS. Phạm Tâm Thành Trường Đại học Hàng hải Việt Nam Người phản biện: TS. Đinh Anh Tuấn GS. TSKH. Thân Ngọc Hoàn

Tóm tắt: Bài báo đề cập đến phương pháp khảo sát đặc điểm ổn định của mô hình trạng thái gián đoạn của máy điện không đồng bộ rotor dây quấn (KĐB-RTDQ) thích hợp với điều khiển thời gian thực. Đặc điểm ổn định của mô hình phụ thuộc vào: Chu kỳ trích mẫu T của hệ thống điều khiển số, tần số công tác và sự thay đổi tham số của động cơ. Các kết quả mô phỏng ban đầu thu được khá khả quan, phục vụ tốt cho các bước thiết kế khâu điều chỉnh bằng các phương pháp tuyến tính và phi tuyến sau này.

Từ khóa: Máy điện không đồng bộ nguồn kép, DFIM, mô hình gián đoạn.

Abstract: The paper presents different methods to stability analysis of discrete- state space model of Doubly-Fed Induction Machine (DFIM) which is suitable with real-time control. These stable characters of this model depend on: sample time of digital system, mission frequency and variable parameter of motor. Simulation result shows that our models has good a performance with followed designs linear controllers and nonlinear controller in next steps.

Keywords: Doubly-Fed Induction Machine, DFIM, discrete-model.

1. Đặt vấn đề

Thực hiện điều khiển số cho máy điện KĐB-RTDQ được thực hiện khá thành công trong các tài liệu.

Mô hình trạng thái gián đoạn (TTGĐ) trên hệ tọa độ dq là xuất phát điểm khi thiết kế hệ thống điều khiển (ĐK) thời gian thực và có ý nghĩa quyết định tới chất lượng của hệ thống ĐK số (Digital Control) của máy điện không đồng bộ rotor dây quấn (hay còn gọi là máy điện không đồng bộ nguồn kép). Hình 1.1 thể hiện rất rõ 2 giải pháp để xây dựng mô hình TTGĐ trên hệ tọa độ dq của máy điện KĐB-RTDQ. Bài báo không đi chi tiết vào cách thức thực hiện cụ thể theo 2 giải pháp đã chỉ ra, mà sử dụng mô hình trạng thái gián đoạn của DFIM đã được xây dựng trong tài liệu [2] để tiến hành khảo sát đặc điểm ổn định của mô hình này. Cấu trúc bài báo gồm: Phần mở đầu được trình bày trong mục 1, phần nội dung được đưa ra ở mục 2, mục 2 thể hiện kết quả mô phỏng rất cụ thể và cuối cùng là phần kết luận trong mục 3[1], [2], [3].

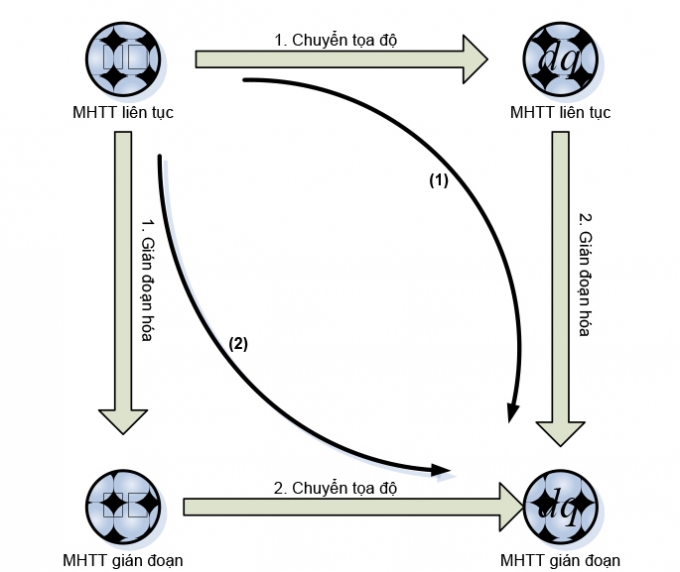Hình 1.1: Các con đường tìm mô hình không gian trạng thái gián đoạn của DFIM  trên hệ tọa độ dq

2. Khảo sát đặc điểm ổn định của mô hình trạng thái gián đoạn của máy điện KĐB-RTDQ

Mô hình trạng thái gián đoạn của máy điện KĐB-RTDQ phục vụ cho mục đích thiết kế hệ thống điều khiển số máy điện KĐB-RTDQ, trước khi thiết kế chúng ta cần tiến hành khảo sát đặc điểm ổn định của mô hình [2].

 

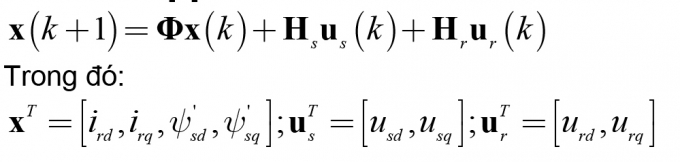 (1)

 

 

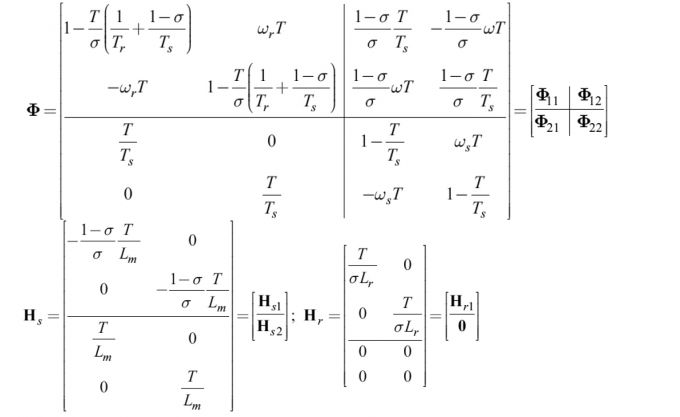(2)

 

 

 

 

 

 

Để thuận tiện cho việc khảo sát đặc điểm ổn định của máy điện nên ta chỉ xét ma trận hệ thống có đặc điểm đối xứng. Ta dễ dàng nhận thấy ma trận Φ chỉ đối xứng trong từng ma trận con nên ta khảo sát đặc điểm ổn định của hệ thống trên từng ma trận con là: Φ₁₁, Φ₁₂,Φ₂₁,Φ₂₂, sau đó đưa ra đánh giá chung cho toàn hệ thống.

Xét một máy điện KĐB-RTDQ có các thông số sau:

 

 

 

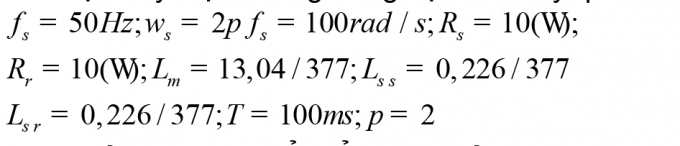2.1. Khảo sát đặc điểm ổn định của máy điện xét trên hệ thống ma trận con Φ₁₁                        

 

 

 

 

 

 

 

Sử dụng phần mềm Matlab ta sẽ thu được quỹ đạo nghiệm số khi T thay đổi được quỹ đạo như Hình 2.1. Giao điểm của quỹ đạo nghiệm với vòng tròn đơn vị là điểm (-0,996+0j) ứng với giá trị T = 0,000123, vậy T_gh = 0,000123(s) điều này hoàn toàn thỏa mãn với các hệ thống truyền động điện hiện đại. Thử lại với T = 100μs ta có vị trí điểm cực và đáp ứng bước nhảy như Hình 2.2.   

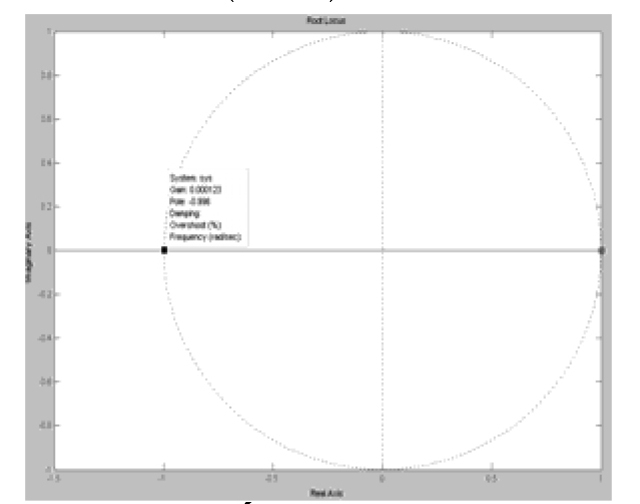Hình 2.1: Quĩ đạo nghiệm số của phương trình đặc trưng khi T thay đổi

 

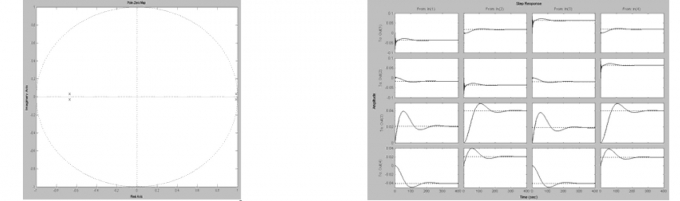Hình 2.2: Vị trí điểm cực và đáp ứng bước nhảy khi T = 100μs

2.1.2. Ảnh hưởng của tần số công tác đến mô hình

Thực hiện tương tự như xét ảnh hưởng của chu kỳ trích mẫu ta có đặc tính như Hình 2.3.

Giao điểm của quỹ đạo với vòng tròn đơn vị là điểm (0,686 + 0,729j) ứng với giá trị:

 

Vậy mô hình hệ thống ổn định khi f_rgh<632(Hz). Khi chu kỳ trích mẫu giảm xuống thì giá trị giới hạn của tần số công tác sẽ tăng lên, với w_r = w_s - w  ta thử với w_s = 200_P(rad/s). Ta có vị trí điểm cực  và đáp ứng bước nhảy của hệ thống như Hình 2.4.

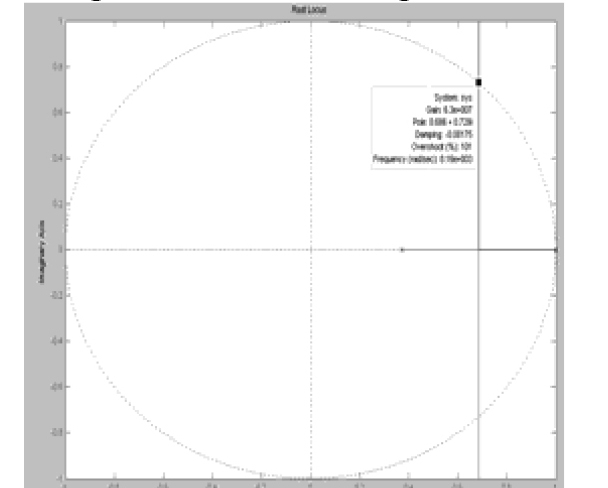Hình 2.3: Quỹ đạo nghiệm số của phương trình đặc trưng khi wr thay đổi

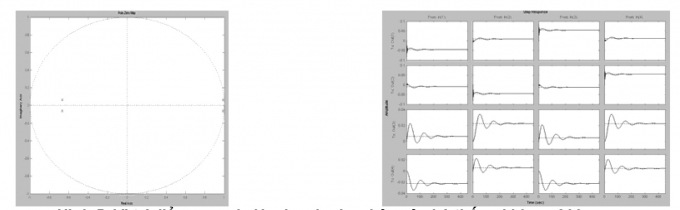Hình 2.4: Vị trí điểm cực và đáp ứng bước nhảy của hệ thống khi ws= 200π

2.1.3. Ảnh hưởng của tham số đến tính ổn định của mô hình

Trong quá trình hoạt động của động cơ cụ thể là điện trở điện cảm stator luôn có sự biến động phụ thuộc vào nhiệt độ và chế độ công tác. Tuy nhiên thực tế, ta có thể coi điện cảm stator là không thay đổi. Vì vậy, ở đây ta chỉ khảo sát điện trở stator đến ảnh hưởng của mô hình động cơ. Ta có phương trình đặc trưng phụ thuộc tham số R_s:

 

 

 

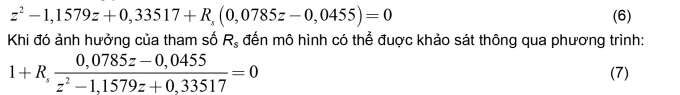Sử dụng phần mềm Matlab ta sẽ thu được đường quỹ đạo nghiệm số khi R_s thay đổi và được kết quả như Hình 2.5.

Giao điểm của quĩ đạo nghiệm với vòng tròn đơn vị là điểm (-0,999+0j) ứng với giá trị giới hạn là 0,102(Ω) < R_s < 20,1(Ω), điều này hoàn toàn thỏa mãn với sự biến thiên của động cơ đang khảo sát trong thực tế. Thử lại với R_s = 10(Ω) ta có vị trí điểm cực và đáp ứng bước nhảy như Hình 2.6.

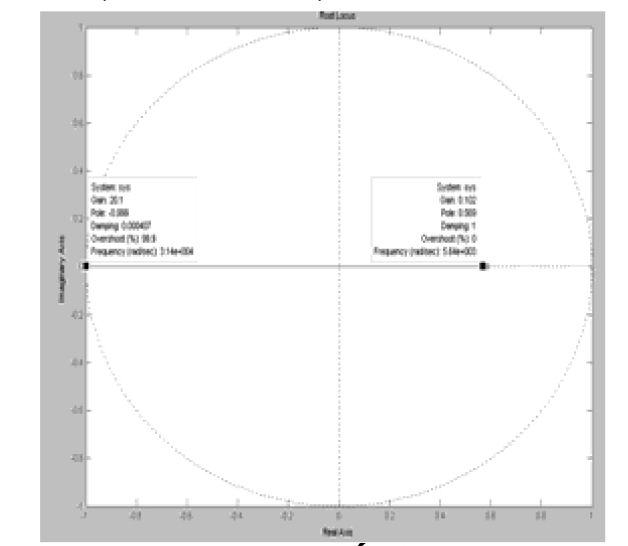Hình 2.5: Quỹ đạo nghiệm số của phương trình đặc trưng khi thay đổi Rs

 

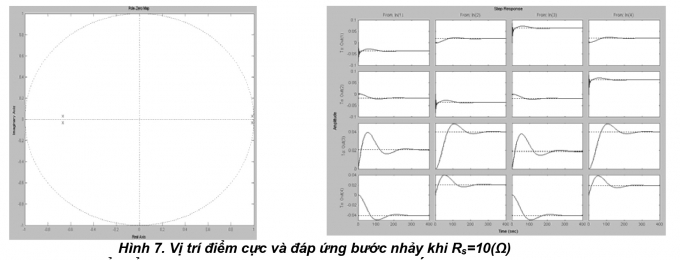Hình 2.6: Vị trí điểm cực và đáp ứng bước nhảy khi Rs = 10(Ω)

 

2.2. Khảo sát đặc điểm ổn định của động cơ khi xét trên hệ thống ma trận con F₁₂

2.2.1. Ảnh hưởng của chu kỳ trích mẫu đến tính ổn định của mô hình

Khi chu kỳ trích mẫu T thay đổi ta có quỹ đạo như Hình 2.7:

 

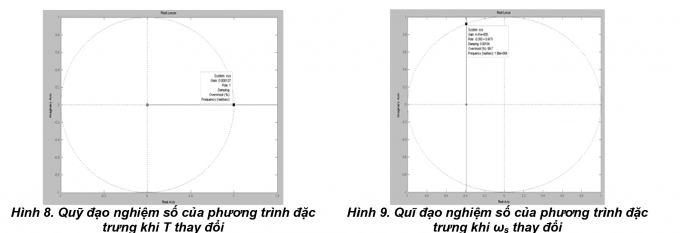2.2.2. Ảnh hưởng của tần số công tác đến tính ổn định của mô hình

Khi w_s thay đổi ta có quỹ đạo như Hình 2.8.

2.3. Khảo sát đặc điểm ổn định của máy điện xét trên hệ thống ma trận con F₂₁

2.3.1. Ảnh hưởng của chu kỳ trích mẫu đến tính ổn định của mô hình

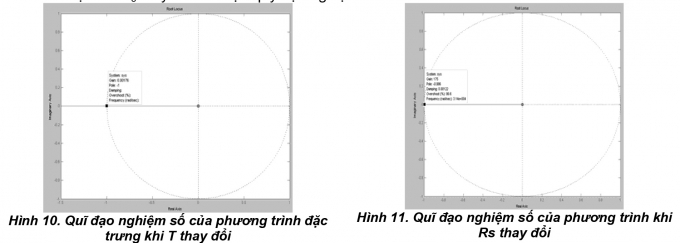
Quỹ đạo nghiệm số khi chu kỳ trích mẫu thay đổi như Hình 2.9.

2.3.2. Ảnh hưởng của tham số đến tính ổn định của mô hình

Tham số điện trở R_s thay đổi ta được quỹ đạo nghiệm số như Hình 2.10:

 

2.4. Khảo sát đặc điểm ổn định của máy điện xét trên hệ thống ma trận con F₂₂

2.4.1. Ảnh hưởng của chu kỳ trích mẫu đến tính ổn định của mô hình

Quỹ đạo nghiệm số khi T thay đổi như Hình 2.11:

 

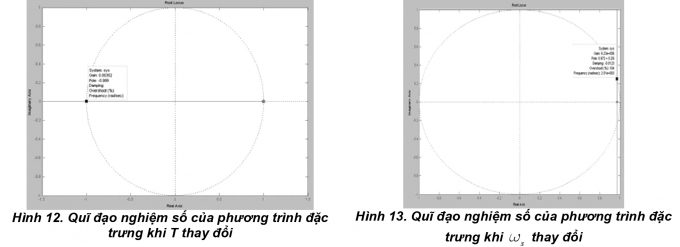2.4.2. Ảnh hưởng của tần số công tác đến tính ổn định của mô hình

Hình 2.12 là quỹ đạo nghiệm số khi w_s thay đổi.

2.4.3. Ảnh hưởng của tham số động cơ đến mô hình

Hình 2.13 là quỹ đạo nghiệm số khi R_s thay đổi

2.5. Nhận xét kết quả mô phỏng

Sau khi ta khảo sát mô hình hệ thống gián đoạn cho từng ma trận hệ thống con ta thấy được để hệ thống làm việc ổn định thì các thông số phải nằm trong khoảng: 0,36 (Ω) < R_s T < 0,000119(s);w_s  < 789(rad/s).

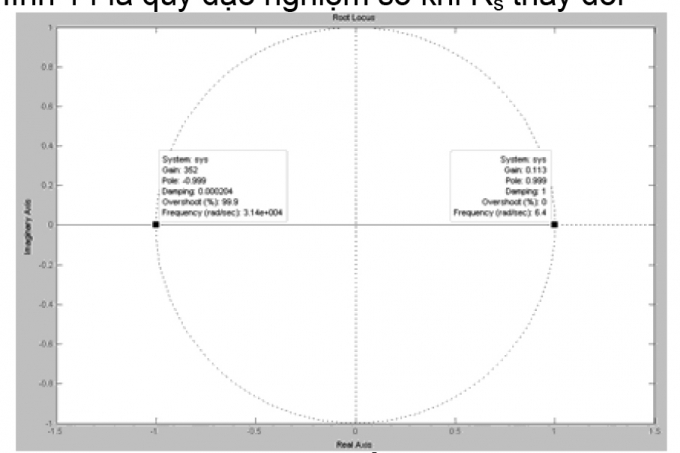Hình 2.13: Quĩ đạo nghiệm số của phương trình đặc trưng khi Rs thay đổi

 

3. Kết luận

Tóm lại, bài báo đã giải quyết được các vấn đề sau:

- Chỉ ra được 2 con đường xây dựng mô hình trạng thái gián đoạn của máy điện KĐB-RTDQ trên hệ tọa độ. Mô hình này để phục vụ cho thiết kế hệ thống điều khiển số máy điện KĐB-RTDQ.

- Vấn đề khảo sát đặc điểm ổn định của mô hình phụ thuộc vào các tham số được thực hiện trong phần 3. Nhìn chung, độ ổn định của mô hình phụ thuộc nhiều vào việc chọn T. Chu kỳ T càng nhỏ, phạm vi ổn định cũng như dải tần số công tác ổn định, sự biến thiên các tham số động cơ (điện trở, điện cảm) sẽ càng lớn. Tuy nhiên, khi T càng nhỏ sẽ làm cho năng suất tính toán tăng lên dẫn đến đầu tư về phần cứng lớn. Vì lý do ấy, người kỹ sư thiết kế sẽ phải đưa ra được một sự lựa chọn dung hòa giữa phạm vi ổn định cần lớn và năng suất tính toán tăng lên (do T bé đi).

Tài liệu tham khảo

[1]. Nguyễn Phùng Quang (1998), Điều khiển tự động truyền động điện xoay chiều ba pha, NXB. Giáo dục.

[2]. Quang. Ng.Ph., Dittrich, J.-A. (2008), Vector control of Three-Phase AC Machines-System Development in the Practice, Springer Berlin Heidelberg.

[3]. Nguyễn Phùng Quang, Joerg-Andreas Dittrich (2004), Truyền động điện thông minh, NXB. Khoa học & Kỹ thuật.

[4]. Nguyễn Phùng Quang (2004), Matlab&Simulink dành cho Kỹ sư điều khiển tự động, NXB. Khoa học & Kỹ thuật.

[5]. Phạm Tâm Thành, Nguyễn Phùng Quang (2011), Khảo sát đặc điểm ổn định của mô hình trạng thái gián đoạn của động cơ đồng bộ kích thích vĩnh cửu, CD tuyển tập Hội nghị Điều khiển & Tự động hóa toàn quốc lần thứ nhất, VCCA-2011, tr.318-323, Hà Nội.

[6]. Phạm Tâm Thành, Nguyễn Phùng Quang (2013), Mô hình trạng thái gián đoạn bilinear của máy điện xoay chiều ba pha theo phương pháp Taylo,  Chuyên san Kỹ thuật Điều khiển & Tự động hóa, số 7, tr.2-7.