Nghiên cứu động lực học cần cẩu tháp dạng cần nằm ngang trong các quá trình nâng vật và thay đổi tầm với

ThS. Nguyễn Thúc Tráng KS. Lê Đức Long Học viện Kỹ thuật Quân sự Người phản biện: GS. TS. Chu Văn Đạt PGS. TS. Nguyễn Văn Bang

TÓM TẮT: Bài báo trình bày tóm tắt việc xây dựng mô hình và công bố một số kết quả nghiên cứu động lực học hệ thống cáp treo vật nâng của cần cẩu tháp dạng cần nằm ngang trong hai quá trình đầu của hành trình làm việc của cần cẩu, từ đó đánh giá ảnh hưởng của các thông số vận hành cần cẩu tháp đến các thông số động lực học của hệ thống cáp treo.

TỪ KHÓA: Cần cẩu tháp, cáp treo, động lực học.

Abstract: This article presents some development models and results on researching dynamics of cable system for tower crane type horizontal  jib in first two working processes. Influence of the controls crane to kinetic parameters of its cable system also evaluated.

KEYWORDS: Tower cranes, slings, dynamics.

1. ĐẶT VẤN ĐỀ

Khi cần cẩu tháp hoạt động, thách thức lớn nhất của nhân viên vận hành cũng như các nhà quản lý và khai thác cần cẩu là kiểm soát sự lắc lư của vật nâng [3]. Vật được cần cẩu tháp nâng chuyển thường có kích thước và khối lượng lớn. Khi cần cẩu chuyển động có gia tốc sẽ xuất hiện lực quán tính. Ngoài chuyển động theo cùng cần cẩu, lực quán tính theo sẽ gây ra chuyển động tương đối của vật nâng đối với cần cẩu, đó là sự lắc lư của hệ thống cáp treo vật nâng xung quanh vị trí cân bằng của nó. Nếu vận hành cần cẩu không hợp lý thì cho dù cần cẩu dừng hẳn, chuyển động tương đối nói trên có thể sẽ có góc lắc lớn và kéo dài trong nhiều giây, thậm trí tới vài phút. Hơn nữa, trước khi được hạ xuống một vị trí xác định, vật nâng cần phải đứng yên hoàn toàn để tránh bị lật đổ gây tai nạn.

Bài báo tóm tắt việc xây dựng mô hình không gian, công bố một số kết quả nghiên cứu động lực học của hệ thống cáp treo vật trong cần cẩu tháp dạng cần nằm ngang. Mô hình có tính đến sức cản của không khí, bỏ qua sự đàn hồi của cần cẩu và sự dãn của dây cáp.

2. MÔ HÌNH CẦN CẨU THÁP

Khi cần cẩu tháp hoạt động, ba thông số luôn được nhân viên vận hành kiểm soát nghiêm ngặt, đó là (Hình 3.1a): Khoảng cách s từ xe đẩy đến cột cần cẩu (tầm với), chiều dài l₁ của đoạn dây cáp treo móc và góc quay y của cần quanh cột. Hệ thống dây cáp gồm hai phần, phần thứ nhất là từ điểm treo O với xe đẩy đến trọng tâm G₁ của khối móc và OG₁ = l₁, phần thứ hai là từ G₁ đến trọng tâm G₂ của vật nâng và G₁G₂ = l₂. Khi cần cẩu hoạt động l₁ thay đổi và l₂ không đổi, OG₁ lắc quanh O với góc lắc θ₂ và G₁G₂ lắc quanh G₁ với góc lắc là θ₂. Hệ thống dây cáp đáp ứng giả định về lý thuyết hệ con lắc vật lý vì các giá trị θ₁,θ₂ thường không quá 8⁰ [4].

3. THIẾT LẬP PHƯƠNG TRÌNH ĐỘNG LỰC HỌC CẦN CẨU THÁP

3.1. Những giả thiết khi xây dựng mô hình động lực học

Để xây dựng phương trình động lực học, ta có những nhận xét sau: Cần cẩu tháp chủ yếu được sử dụng trong các công trình xây dựng có chiều cao lớn. Để chống rung lắc trong hoạt động, thân tháp sẽ được neo chặt với công trình bằng các gông thép chịu lực. Mặt khác, nếu cần nâng được lắp đủ hai dây cương, vật nâng có khối lượng nhỏ so với khối lượng nâng cho phép và được vận hành bởi các thông số vận hành khuyến cáo của nhà sản xuất, thì biến dạng của thân tháp và cần nâng thường rất nhỏ. Khối móc được treo với xe đẩy bởi bốn dây cáp kiểu tháp, vì thế khả năng khối móc xoay quanh trục OG₁ rất thấp. Vì vậy, xem cần và cột tháp là tuyệt đối cứng, bỏ qua góc xoắn và sự dãn của dây cáp,  coi điểm treo l₂ trùng với G₁.

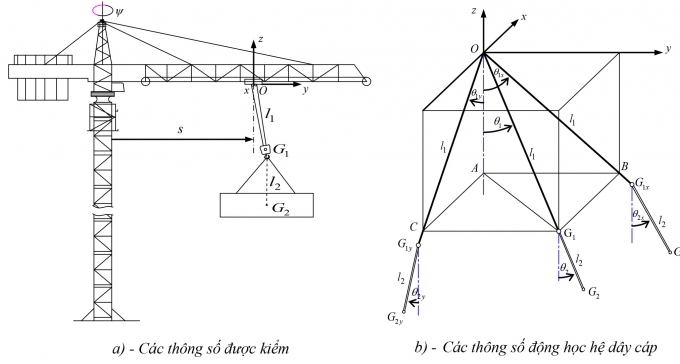Hình 3.1: Mô hình cần cẩu tháp dạng cần nằm ngang

 3.2. Lực tác động lên móc và vật nâng trong quá trình nâng vật và thay đổi tầm với

Gắn vào điểm treo O một hệ trục tọa độ Oxyz, trục z thẳng đứng, trục y dọc theo cần. Gọi m₁, m₂ là khối lượng của móc, vật nâng. Khi cần cẩu hoạt động trong các giai đoạn nâng vật và thay đổi tầm với, móc và vật nâng chịu tác động của các lực và lực quán tính sau.

3.2.1. Trọng lượng của móc và của vật nâng

3.2.2. Lực quán tính theo xe đẩy: Xuất hiện khi xe đẩy chuyển động có gia tốc (giai đoạn tăng tốc và giai đoạn phanh), được xác định bởi                                            

       có đường tác dụng lần lượt đi qua trọng tâm móc, vật nâng và có phương song song với trục y

 

 

 

 

 

 

 

 

  

3.3. Phương trình động lực học

Các thành phần lực đã xác định ở trên đều có phương song song với ít nhất một trong hai mặt phẳng (x - z), (y - z). Mặt khác, l₁ thường rất lớn, còn θ₁,θ₂ và góc giữa OG₁ cũng như G₁G₂ với các mặt phẳng (x - z), (y - z) là nhỏ, cho nên độ dài hình chiếu vuông góc của l₁, l₂ trên các mặt phẳng (x - z), (y - z) xấp xỉ bằng l₁, l₂ tương ứng. Gập l₁ và l₂ trong các mặt phẳng lần lượt chứa nó và vuông góc với mặt phẳng (y –z) về vị trí nằm trong (y –z)(Hình 3.1b); gập l₁ và l₂ trong các mặt phẳng lần lượt chứa nó và vuông góc với mặt phẳng (x - z) về vị trí nằm trong (x - z). Gọi A, B, C lần lượt là hình chiếu thẳng góc của G₁ lên phương thẳng đứng qua O, (y - z), (x - z). Rõ ràng,  B  thuộc OG_1x, C thuộc OG_1y và AO, AB, AC là ba kích thước của hình hộp chữ nhật có đường chéo là OG₁ = l₁. Gọi θ_1x,θ_2x lần lượt là góc giữa OG_1x,G_1xG_2xvới phương thẳng đứng trong mặt phẳng (y - z); θ_1y ,θ_2y lần lượt là góc giữa OG_1y ,G_1yG_2yvới phương thẳng đứng trong mặt phẳng (x - z). Từ hình hộp nói trên, ta có:

 

 

 

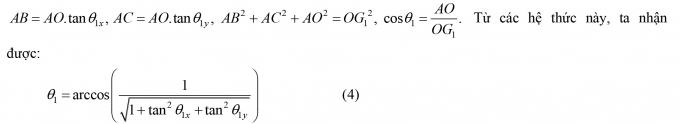Một cách tương tự, ta cũng có:

 

 

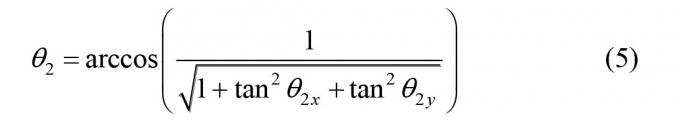Tại mỗi thời điểm, chuyển động của hệ thống cáp treo được xem là tổng hợp của hai chuyển động phẳng của nó trong các mặt phẳng (x - z), (y - z).

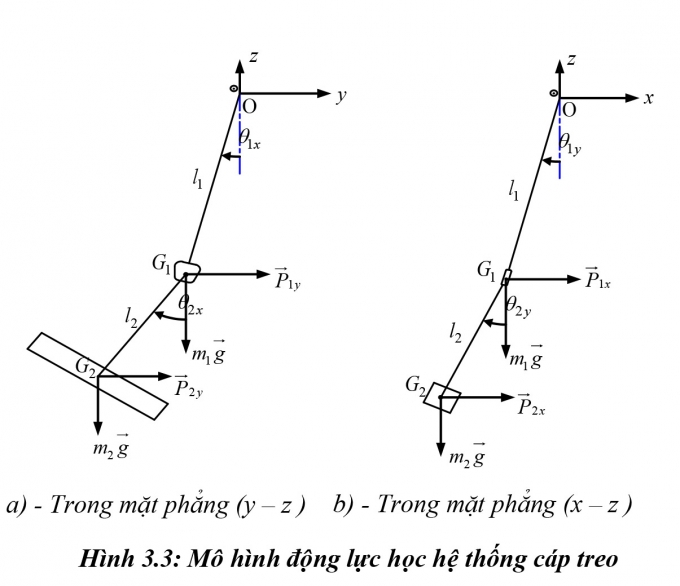Xét hệ trong mặt phẳng (y - z) (Hình 3.3.a): Hệ có hai bậc tự do ứng với hai tọa độ suy rộng θ_1x,θ_2x . Sử dụng phương trình Lagrange II để thiết lập phương trình vi phân chuyển động của hệ:

 

 

 

 

 

 

 

 

 

 

 

 

 

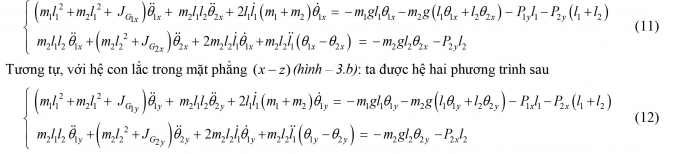4. MÔ PHỎNG SỐ TRÊN CẦN CẨU THÁP QTZ63

Với bộ thông số đầu vào xác định,  hệ phương trình  (11) và (12) được giải gần đúng bằng phương pháp Runge - Kutta bậc bốn trên nền Matlab. Nghiệm hệ (11) là θ_1x,θ_2x và nghiệm hệ (12) là θ_1y ,θ_2y ; các góc lắc θ₁,θ₂ tại mỗi thời điểm lần lượt được xác định theo (4) và (5). Các thông số đầu vào của vật nâng chuyển, cần cẩu tháp QTZ63 và kết quả mô phỏng trong các mục sau đây.

4.1. Vật nâng chuyển

Vật nâng là dầm bê tông cốt thép dài 5m, kích thước mặt cắt ngang 0,3×0,5m, chiều dài dầm theo phương thẳng đứng, được nâng chuyển từ trạng thái tĩnh, chính tâm (O, G₁, G₂ thẳng đứng), từ mặt đất lên độ cao 62m và từ tầm với ban đầu 10m đến tầm với 43m. Các thông số đầu vào như sau:

 

 

4.2. Chế độ vận hành cần cẩu

Với vật nâng đã chọn, chế độ vận hành trên cần cẩu QTZ63 theo khuyến cáo của nhà sản xuất [2] là: Vận tốc trung bình nâng vật  i_1tb = 1.2m/s; vận tốc trung bình xe đẩy   ` `   _tb= 0.3m/s.

Ở đây khảo sát hai trường hợp, thứ nhất là quá trình nâng vật kết thúc rồi mới đến quá trình thay đổi tầm với, thứ hai là phối hợp cả hai quá trình trên. Trong trường hợp thứ hai, quá trình thay đổi tầm với bắt đầu hoạt động từ giây thứ 10 (khi đó vật nâng đã ở một độ cao khoảng 10m). Thời gian các giai đoạn: Tăng tốc, bình ổn, phanh và giá trị gia tốc trong mỗi quá trình nâng, thay đổi tầm với được chọn trong Bảng 4.1:

Bảng 4.1. Thời gian và gia tốc các giai đoạn trong từng quá trình

Quá trình nâng vật				Quá trình thay đổi tầm với
Giai đoạn	Thời gian (s)	Gia tốc (m/s2)		Giai đoạn	Thời gian (s)	Gia tốc (m/s2)
Tăng tốc	5	-0,24		Tăng tốc	3	0.1
Bình ổn	47	0		Bình ổn	107	0
Phanh	3	0,4		Phanh	3	-0.1

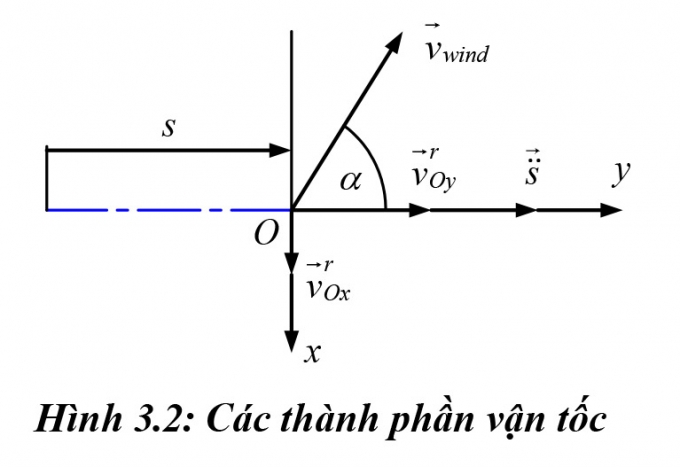
4.3. Vận tốc và quy luật gió

Quy luật gió được giả định là tuần hoàn, chu kỳ 5 giây. Hướng gió không đổi và bỏ qua thành phần rối của gió. Ở độ cao dưới 10m, giá trị vận tốc gió theo các mốc thời gian: 0, 1, 2, 3, 4, 5 giây lần lượt là: 4, 5, 6, 5, 3, 4 m/s. Các giá trị của vận tốc gió sau mỗi bước thời gian được xác định bằng phương pháp nội suy tuyến tính.

Càng lên cao vận tốc gió càng lớn [1], ở độ cao từ 10m đến 40m vận tốc gió gấp 1,1 đến 1,6 lần so với vận tốc gió ở độ cao dưới 10m; độ cao từ 41m đến 70m vận tốc gió gấp 1,1 đến 1,3 lần so với độ cao 40m.

4.4. Kết quả và bàn luận

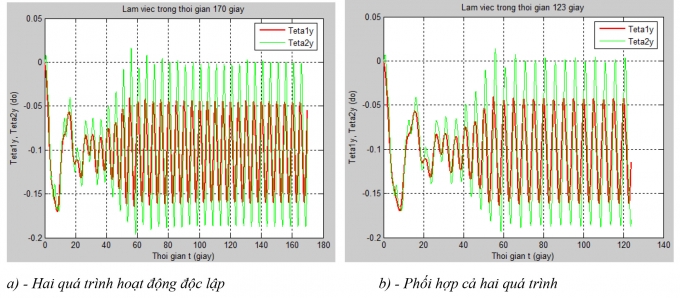
Kết quả mô phỏng từ Hình 4.1 đến Hình 4.3. Từ kết quả nhận được ta có các nhận xét sau: Vì khối lượng móc nhỏ hơn rất nhiều so với khối lượng vật nâng, nên từ đồ thị Hình 4.3 ta thấy, tốc độ lắc của l₁ và l₂ xấp xỉ bằng nhau trong mọi thời điểm; góc lắc cáp treo vật thường lớn hơn góc lắc cáp treo móc. Do α = 0^o nên gió luôn theo phương x (thành phần vận tốc gió theo phương y luôn bằng không), quan sát đồ thị Hình 4.1a và Hình 4.2a trong quá trình nâng vật (quá trình thay đổi tầm với chưa hoạt động), ta thấy các góc lắc trong mặt phẳng (x – z) lớn hơn hẳn so với góc lắc trong mặt phẳng (y – z). Các giai đoạn tăng tốc, phanh xe đẩy trong quá trình thay đổi tầm với đều xuất hiện quán tính nên các góc lắc lớn hơn hẳn so với giai đoạn xe đẩy chuyển động bình ổn. Trường hợp vật nâng có khối lượng nhỏ, nếu phối hợp hoạt động của hai quá trình thì thời gian làm việc nhỏ hơn rất nhiều, trong khi đó góc lắc lớn nhất không chênh lệch nhiều.

Trong trường hợp phối hợp hoạt động của hai quá trình, với mốc thời gian và các thông số đã lựa chọn, kết quả trên Hình 4.3b cho ta θ_1max = 0,75^o, θ_2max = 0,86^o và xảy ra trong giai đoạn phanh xe đẩy. Khi đó, l₁ = 8,2m và trọng tâm G₂ của vật nâng lệch ngang khỏi vị trí cân bằng tĩnh của nó một khoảng:

 

 

Hình 4.1: Giá trị các góc lắc trong mặt phẳng (y - z)

 

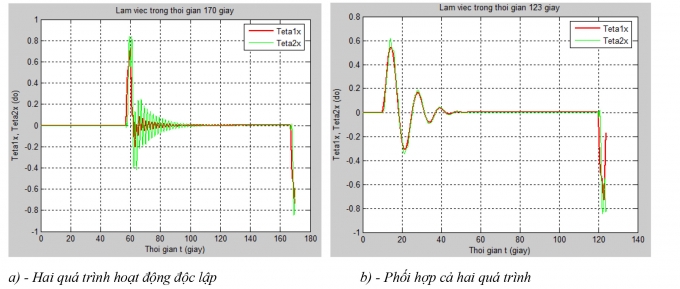
Hình 4.2: Giá trị các góc lắc trong mặt phẳng (x - z)

 

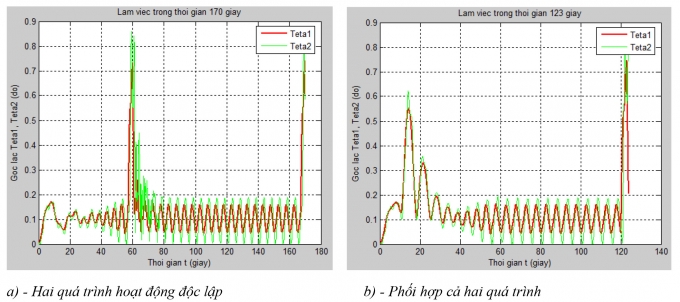Hình 4.3: Giá trị các góc lắc trong không gian

5. KẾT LUẬN

Bài báo xây dựng được một mô hình, thiết lập được phương trình động lực học để mô tả hành vi của cần cẩu tháp trong quá trình nâng vật và thay đổi tầm với, đã xác định được góc lắc của hệ thống dây cáp theo các thông số vận hành cần cẩu trong hai chế độ vận hành. Kết quả nghiên cứu góp phần giúp các nhà quản lý và nhân viên vận hành hiểu sâu sắc hơn nữa sự hoạt động của cần cẩu, từ đó nhằm giảm thiểu tan nạn và nâng cao năng xuất lao động khi vận hành cần cẩu tháp. Tuy nhiên, do phạm vi của bài báo nên kết quả đã công bố còn hạn chế, chưa phản ánh đầy đủ vị trí của vật nâng trong quá trình cần cẩu hoạt động.

Tài liệu tham khảo

[1]. Tạ Văn Đa, Tài nguyên năng lượng gió trên lãnh thổ Việt Nam, Tuyển tập báo cáo Hội thảo khoa học lần thứ 10, Viện KHKTTV & MT.

[2]. Nguyễn Đăng Điệm (2014), Cần trục tháp xây dựng, NXB. Xây dựng.

[3]. Amatucci, E., Bostelman, R., Dagalakis, N., Tsai, T (September 1997), Summary of Modeling and Similation for NIST RoboCrane Applications, Proceedings of the 1997 Deneb International Simulation Conference and Technology Showcase, Detroit, MI.

[4]. Shih-Chung Jessy Kang, Eduardo Miranda (April 2009), Numerical Methods to Simulate and Visualize Detailed Crean Activities, Article in computer- Aided Civil and Infrastructure Engineering.