Phân tích tấm uốn chịu tải trọng ngẫu nhiên bằng phương pháp mô phỏng Monte Carlo

TS. Tạ Duy Hiển ThS. Nguyễn Thị Nhung ThS. Lê Quỳnh Nga Trường Đại học Giao thông vận tải Người phản biện: TS. Nguyễn Thị Cẩm Nhung TS. Nguyễn Trung Kiên

TÓM TẮT: Bài báo nghiên cứu tính tấm uốn chịu tải trọng ngẫu nhiên bằng cách kết hợp phương pháp đẳng hình học với giải thuật mô phỏng ngẫu nhiên Monte Carlo. Trường ngẫu nhiên của tải trọng được giả thiết có dạng đồng nhất Gauss và được mô phỏng bằng phép biểu diễn phổ. Các đặc trưng ngẫu nhiên của chuyển vị của tấm được khảo sát cụ thể qua các ví dụ, ảnh hưởng của các tham số ngẫu nhiên của tải trọng cũng được đánh giá chi tiết. 

TỪ KHÓA: Phân tích đẳng hình học, tấm uốn, tải trọng ngẫu nhiên.

ABSTRACT: This paper studied behavior of bending plate subjected to random loading by using Isogeometric Analysis method (IGA) and Monte Carlo simulation. Stochastic fields of loading were modeled as Gaussian stochastic fields. Random field was simulated by spectral representations. The response variability of displacement fields is investigated by numerical example. The effect of randomness parameters of loading on response variability were discussed in detail.

KeywordS: Stochastic isogeometric analysis, bending plate, random loading.

1. ĐẶT VẤN ĐỀ

Trong thực tế, các tải trọng đưa vào thiết kế thường chúng ta phải thống kê và mô tả chúng theo một quy luật nào đó để đánh giá ảnh hưởng của chúng đến kết cấu. Một số phương pháp tính toán kết cấu với tham số ngẫu nhiên đã được một số tác giả nghiên cứu dựa trên phương pháp phần tử hữu hạn [1-3].  Một số tác giả [4-8] đã sử dụng phương pháp phần tử hữu hạn ngẫu nhiên tính bài toán tấm với tham số ngẫu nhiên của tính chất vật liệu, đặc trưng hình học...

Giáo sư Thomas Hughes và cộng sự [9, 10] đã đề xuất  phương pháp phân tích đẳng hình. Nó sử dụng các hàm nội suy spline không đều để xấp xỉ hình học và các trường chuyển vị, vì thế thuận tiện trong việc phân tích kết cấu lẫn mô phỏng hình học, giảm sai số khi xấp xỉ hình học. Nó có ứng dụng lớn trong việc phân tích thiết kế các kết cấu có dạng hình học phức tạp như kết cấu vỏ máy bay, kết cấu máy...

Bài báo sử dụng phân tích đẳng hình học cho bài toán tấm uốn chịu tải trọng ngẫu nhiên bằng thuật giải mô phỏng Monte Carlo, từ đó tìm được các đặc trưng xác suất của trường chuyển vị.

2. CƠ SỞ PHƯƠNG PHÁP ĐẰNG HÌNH HỌC TRÊN CƠ SỞ CÁC HÀM XẤP XỈ SPLINE [9, 10]

2.1. Véc-tơ nút và các hàm cơ bản

Phương pháp phân tích đẳng hình học sử dụng hàm NURBS (non-uniform rational B-spline) để mô tả hình học và xấp xỉ các chuyển vị. Hàm NURBS được xây dựng dựa trên các hàm cơ bản. Các hàm cơ bản này lại được xây dựng từ véc-tơ nút. Xét các tham số trên miền một chiều ξ ∈[0,1], véc-tơ nút định nghĩa như sau:

 

 

Trong đó: p - Bậc đa thức; n - Số hàm cơ bản B-spline.

Hàm cơ bản B-spine được xây dựng theo kiểu truy hồi như sau

 

 

                                                                                                                                                                                    

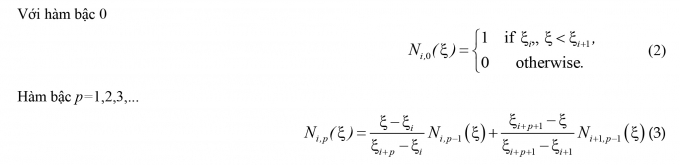2.2. Đường cong và mặt cong B-spine

Đường cong và mặt cong B-spine được xây dựng từ các điểm điều khiển B_i và các hàm cơ bản B-spine.

Đường cong B-spine:

 

Mặt cong B-spine:

 

2.3. Hàm NURBS

Từ hàm B-spine người ta tổng quát hóa thành hàm NURBS để nó có thể mô tả chính xác hơn một số dạng hình như đường còn, mặt cong eliptic...

Hàm hữu tỷ cơ bản:

 

 

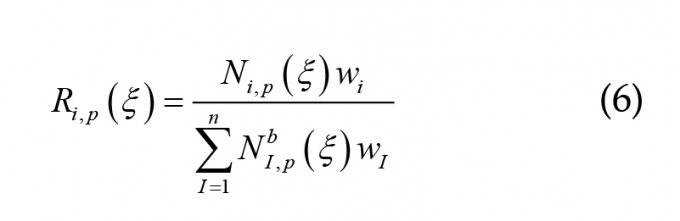Trong đó: w_i- Trọng số.

Hàm NURBS mô tả đường cong, mặt cong:

Đường cong:

 

 

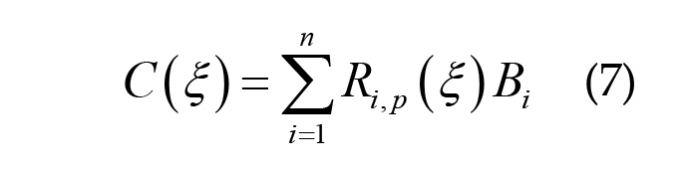Mặt cong:

 

 

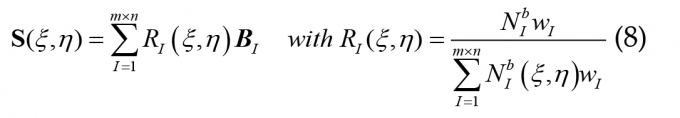Hình 2.1 mô tả mặt cong thực mầu xanh qua các điểm điều khiển mầu đỏ.

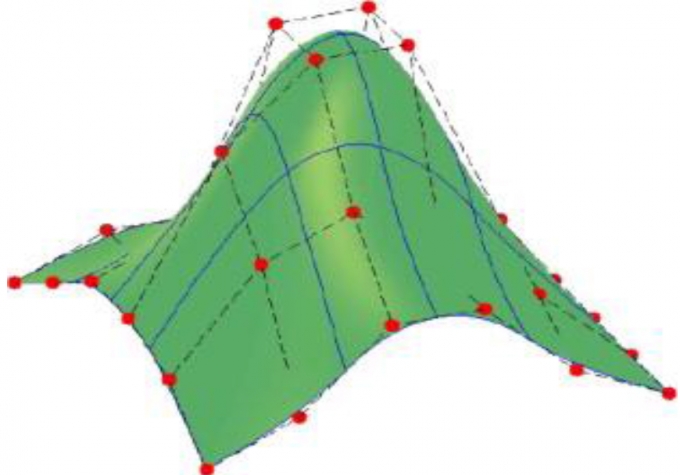Hình 2.1: Mô phỏng mặt cong bằng hàm NURBS [11]

 3. TÍNH TẤM UỐN CHỊU TẢI TRỌNG NGẪU NHIÊN SỬ DỤNG PHƯƠNG PHÁP PHÂN TÍCH ĐẲNG HÌNH HỌC KẾT HỢP MÔ PHỎNG MONTE CARLO

Để thiết lập các phương trình ứng xử của tấm, trong nghiên cứu này lý thuyết tấm cổ điển được sử dụng.  Công thức trường chuyển vị của tấm như sau:

 

 

 

 

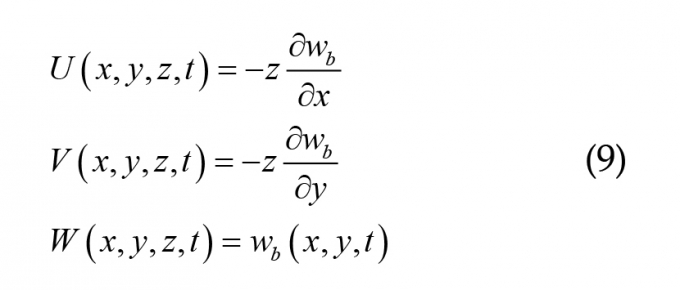Trong đó: U,V,W  - Các chuyển vị tại tọa độ (x,y,z); w_b - Độ võng tại mặt trung bình của tấm

Mối quan hệ ứng suất - biến dạng:

 

 

 

 

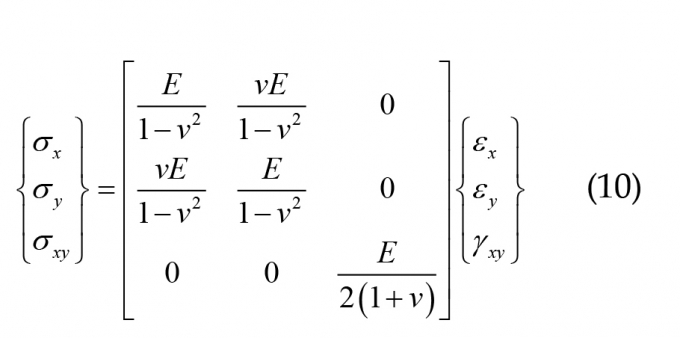Trường chuyển vị  U được xấp xỉ bằng cách sử dụng các hàm NURBS như sau:

 

 

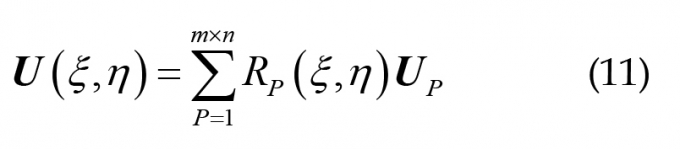Trong đó:U_p - Véc-tơ tham số chuyển vị tại nút điều khiển P:

 

      

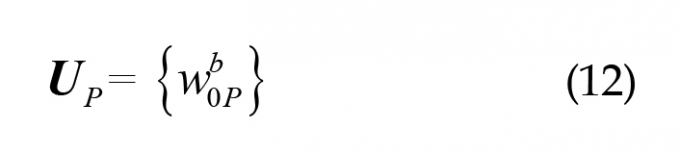Phương trình cơ bản của tấm sử dụng các hàm NURBS:

KU = F (13)

Trong đó: K,U,F tương ứng là ma trận độ cứng của kết cấu, véc-tơ tham số chuyển vị, véc-tơ tải trọng.

Trong nghiên cứu này, tải trọng được nghiên cứu là dạng phân phối đều trên tấm. Tính chất ngẫu nhiên của tải trọng được giả thiết là trường ngẫu nhiên đồng nhất phân phối Gauss có dạng:

 

 

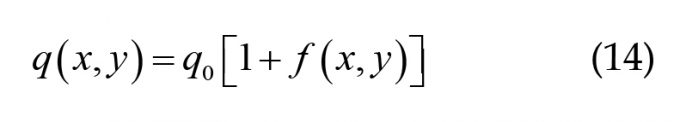Trong đó: q₀ - Giá trị trung bình của tải trọng phân phối đều; f(x,y) - Trường ngẫu nhiên đồng nhất với trung bình bằng không. Giả sử trường này có hàm tự tương quan như sau:

 

 

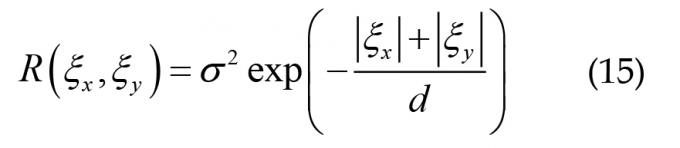Trong đó: ξ_x,ξ_y - Khoảng cách giữa hai điểm xét; d - Tham số khoảng cách tương quan và σ - Hệ số biến động của trường ngẫu nhiên.

Để thực hiện thuật toán mô phỏng Monte Carlo, ta sử dụng phương pháp biểu diễn phổ để mô phỏng trường ngẫu nhiên của tải trọng:

 

 

 

 

 

 

 

 

 

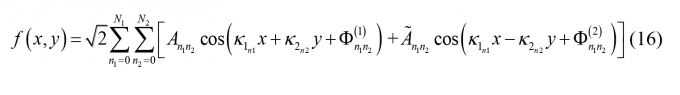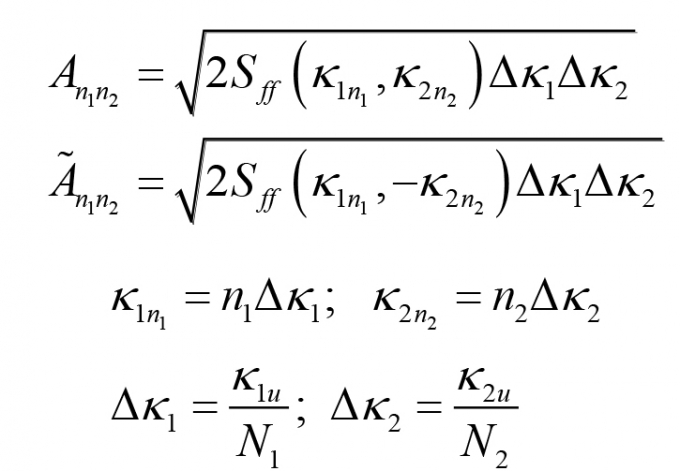Trong đó:

Góc pha Φ_n1n2⁽¹⁾, Φ_n1n2⁽²⁾ được gieo ngẫu nhiên trong khoảng [0, 2π], S_ff - Hàm mật độ phổ suy ra từ hàm tự tương quan R (ξ_x,ξ_y) .

Mỗi lần gieo mẫu mô phỏng ta có giá trị của hàm f(x,y), từ đó có giá trị xác định của tải trọng, xác định được chuyển vị của tấm bằng phân tích đẳng hình học. Tính toán nhiều lần như thế ta sẽ thu được kết quả thông kê của các chuyển vị như giá trị trung bình, phương sai, từ đó tính được hệ số biến động của chuyển vị.

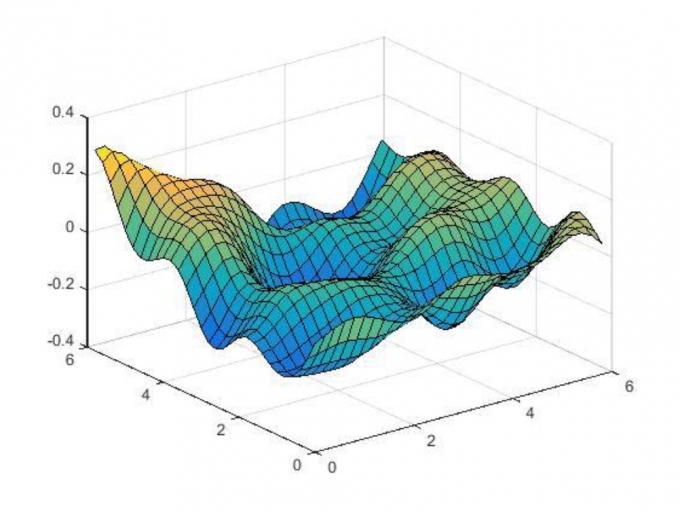Hình 3.1: Mô phỏng trường ngẫu nhiên f(x,y) bằng cách biểu diễn phổ

Hệ số biến động COV của chuyển vị tại giữ tấm được xác định bằng tỷ số độ lệch chuẩn chia cho giá trị trung bình:

 

 

4. VÍ DỤ TÍNH TOÁN

Tấm chữ nhật với điều kiện biên ngàm có cạnh a = 20(cm), b = 20(cm), chiều cao h = 1(cm), mô-đun đàn hồi E = 200(GPa), ν = 0,3. Tải trọng phân bố đều có cường độ trung bình:

Hệ số biến động của trường ngẫu nhiên tải trọng: σ = 0,1.

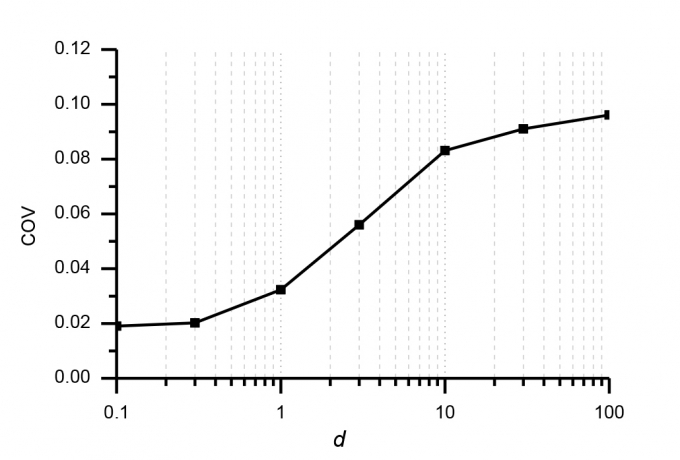Hình 4.1: Ảnh hưởng của tham số chiều dài d đến COV

Sử dụng lưới 8 x 8 cho phân tích đẳng hình học kết hợp với mô phỏng Monter Carlo. Kết quả từ mô phỏng Monte Carlo với số lượng lặp 5.000 mẫu.

Kết quả mối quan hệ tham số khoảng cách tương quan d của trường ngẫu nhiên tải trọng và hệ số biến thiên COV của chuyển vị được thể hiện trên Hình 4.1, qua đó ta thấy COV tỷ lệ thuận với tham số d và khi d khá lớn thì COV bằng giá trị hệ số biến động của trường ngẫu nhiên tải trọng. Kết quả của hai cách tính toán rất gần nhau tại vùng giá trị d lớn.

5. KẾT LUẬN

Nghiên cứu này đã đề xuất cách tính các đặc trưng về chuyển vị của tấm chịu tải trọng ngẫu nhiên bằng phân tích đẳng hình học kết hợp với mô phỏng Monter Carlo. Sự biến thiên COV của chuyển vị đã được khảo sát qua tham số chiều dài d của trường ngẫu nhiên của tải trọng, kết quả cho thấy khi chiều dài rất lớn thì COV của chuyển vị gần sát với COV của trường ngẫu nhiên của tải trọng.

Tài liệu tham khảo

[1]. G. Stefanou (2009), The stochastic finite element method: Past, present and future, Computer Methods in Applied Mechanics and Engineering, 198, 1031-1051.

[2]. A. Der Kiureghian (1988), J.-B. Ke, The stochastic finite element method in structural reliability, Probabilistic Engineering Mechanics, 3, 83-91.

[3]. R.G. Ghanem, P.D. (1991), Spanos, spectral stochastic finite-element formulation for reliability-analysis, J. Eng. Mech.-ASCE, 117 2351-2372.

[4]. H.-C. Noh (2004), A formulation for stochastic finite element analysis of plate structures with uncertain Poisson’s ratio, Computer Methods in Applied Mechanics and Engineering, 193, 4857-4873.

[5]. A. Lal, K.R. Jagtap, B.N. Singh (2013), Post buckling response of functionally graded materials plate subjected to mechanical and thermal loadings with random material properties, Applied Mathematical Modelling, 37, 2900-2920.

[6]. H.-C. Noh, T. Park (2011), Response variability of laminate composite plates due to spatially random material parameter, Computer Methods in Applied Mechanics and Engineering, 200, 2397-2406.

[7]. M. Talha, B.N. Singh (2014), Stochastic perturbation-based finite element for buckling statistics of FGM plates with uncertain material properties in thermal environments, Composite Structures, 108, 823-833.

[8]. B.N. Singh, A. Lal, R. Kumar (2008), Nonlinear bending response of laminated composite plates on nonlinear elastic foundation with uncertain system properties, Engineering Structures, 30, 1101-1112.

[9]. C.J. Austin, T.J.R. Hughes, Y. Bazilevs (2009), Isogeometric Analysis: Toward Integration of CAD and FEA, Wiley.

[10]. T.J.R. Hughes, J.A. Cottrell, Y. Bazilevs (2005), Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement, Computer Methods in Applied Mechanics and Engineering, 194  4135-4195.

[11]. L.V. Tran, A.J.M. Ferreira, H. Nguyen-Xuan (2013), Isogeometric analysis of functionally graded plates using higher-order shear deformation theory, Composites Part B: Engineering, 51, 368-383.