Phân tích, lựa chọn công thức xác định sức kháng của cọc ống thép sử dụng trong công trình cầu ở Việt Nam

TS. Đỗ Hữu Thắng ThS. Nguyễn Thái Khanh Viện Khoa học và Công nghệ Giao thông vận tải Người phản biện: TS. Nguyễn Việt Khoa ThS. Bùi Xuân Học

TÓM TẮT: Bài báo trình bày một số kết quả nghiên cứu xác định công thức tính toán sức chịu tải cọc ống thép sử dụng trong công trình cầu ở Việt Nam. Báo cáo đã trình bày đặc trưng ứng xử của mũi cọc ống thép hở mũi, phân tính các công thức tính sức chịu tải cọc ống thép theo Tiêu chuẩn thiết kế cầu 22TCN 272-05, Tiêu chuẩn Hàn Quốc KGS 2003 và Tiêu chuẩn Nhật Bản JRA 2002. Trên cơ sở so sánh các kết quả tính theo các công thức cùng với các kết quả thử nghiệm cọc ở hiện trường cho một công trình cụ thể, bài báo nhận thấy kết quả tính theo tiêu chuẩn Nhật Bản tương đối phù hợp với kết quả thí nghiệm. Tuy nhiên, hiện nay chỉ mới có công thức theo KGS 2003 được xác định hệ số sức kháng theo lý thuyết độ tin cậy. Tác giả đã tiến hành định chuẩn hệ số sức kháng theo công thức JRA 2002, dựa vào phương pháp FOSM, trên cơ sở phân tích 29 số liệu thẻ tải cọc của Nhật Bản. Bài báo kiến nghị áp dụng cả công thức JRA 2002 và KGS 2003 vào tính toán móng cọc ống thép, đồng thời đề xuất thu thập thêm số liệu thử nghiệm hiện trường để xác định hệ số sức kháng cho công thức JRA 2002 theo lý thuyết độ tin cậy.

TỪ KHÓA: Cọc ống thép, sức kháng, công trình cầu.

Abstract: This paper presents some preliminary results of a study to identify a formula to estimate the bearing capacity of steel pipe piles used in bridges in Vietnam. The report presented the characteristic behavior of the open-end steel pipe pile, analyzed the formula for calculating the bearing capacity of steel pipe piles under the Specification for bridge design 22TCN 272-05, Korean Standard KGS 2003, and Japanese Standards JRA 2002. Based on the comparison of the results calculated by the above formula with the results of the field test pile for a specific project, the paper found that the results calculated by Standard Japanese equivalent to the experimental results. However, only the formula under 2003 KGS determination of resistance to reliability theory. This paper propose do apply the formula JRA 2002 and KGS 2003 to calculate steel pipe pile foundation, and propose to collect field tests data to determine resistance coefficients for the formula in the 2002 JRA based on reliability theory.

KEYWORDS: Steel pipe piles, resistance, bridges.

1. Đặt vấn đề

Trên thế giới, móng cọc ống thép là một loại móng đã được sử dụng để có thể đáp ứng được các điều kiện địa chất phức tạp, độ tin cậy của kết cấu móng trong xây dựng khá cao. Từ đầu thế kỷ XX, móng cọc ống thép đã được sử dụng tại nhiều nước như Đức (1930), Nga (1931)... Năm 1954, móng cọc ống thép dạng đơn đã được sử dụng trong xây dựng bến cảng Shiogama (Nhật Bản). Năm 1964, hệ vòng vây cọc ống thép lần đầu tiên được sử dụng tại Nhật Bản. Năm 1969, móng cọc ống thép đã được áp dụng cho cầu vượt sông Ishikari ở Hokkaido. Tính đến nay, hàng nghìn móng cọc ống thép đã được xây dựng ở Nhật Bản, châu Âu, châu Mỹ...

Những năm gần đây, móng cọc ống thép đã được áp dụng vào một số công trình cầu ở Việt Nam cho hệ thống phụ trợ thi công cũng như kết cấu dưới của mố trụ cầu Nhật Tân. Trong dự án đường ô tô Tân Vũ - Lạch Huyện, kết cấu móng cọc ống thép cũng sẽ được sử dụng cho các công trình cầu. Với các dự án có nguồn vốn ODA từ Nhật Bản, phương án móng cọc ống thép có xu hướng sẽ ngày càng được xem xét, sử dụng.

Trong thực tế xây dựng ở các nước, cả cọc ống thép hở mũi và kín mũi đều được áp dụng. Các nghiên cứu đều cho thấy, ứng xử của cọc hở mũi có những đặc điểm khác biệt so với cọc kín mũi. Các kết quả nghiên cứu khác cho thấy, dạng thức đóng cọc là một yếu tố/thành phần quan trọng trong sức kháng đóng cọc. Nếu một cọc được đóng theo dạng thức lõi hoàn toàn (hay hoàn toàn không tạo nút), đất chui vào trong cọc theo đúng tốc độ xuyên của cọc. Trong khi đó, nếu cọc được đóng dưới dạng thức tạo nút (plugged) hoặc tạo nút một phần (partially plugged), một nút đất sẽ dính bám vào mặt trong của cọc, ngăn ngừa đất chui thêm vào trong cọc. Một cọc được đóng dưới dạng thức tạo nút sẽ ứng xử tương tự như cọc kín mũi.

Như vậy, có thể thấy rằng, cọc kín mũi là cọc chiếm chỗ, ứng xử tương tự như các cọc đóng bình thường. Trong khi đó, cọc hở mũi ứng xử phức tạp hơn, thường là nằm giữa cọc không chiếm chỗ và cọc chiếm chỗ. Do đó, việc nghiên cứu ứng xử của cọc ống thép hở mũi để đưa ra các công thức tính toán phù hợp đã thu hút được sự quan tâm của rất nhiều nhà khoa học cũng như các hiệp hội về móng cọc trên thế giới.

2. CÁC CÔNG THỨC TÍNH TOÁN SỨC CHỊU TẢI CỌC ỐNG THÉP

2.1. Tiêu chuẩn thiết kế cầu đường bộ của Hiệp hội Đường bộ Nhật Bản

- Sức kháng mũi cọc: Theo tiêu chuẩn này, sức chịu tải mũi cọc ống thép hở được rút ra từ việc phân tích rất nhiều các số liệu thí nghiệm hiện trường ở Nhật Bản. Theo đó, sức chịu tải mũi cọc Q_b (kN) phụ thuộc chủ yếu vào độ sâu cọc ngàm vào trong lớp đất tốt (công thức 1):

 

 

 

 

2.2. Theo Tiêu chuẩn thiết kế cầu 22TCN272-05 (cập nhật AASHTO 2012)

Theo mục “10.7.3. Sức kháng ở trạng thái giới hạn cường độ”, sức kháng của cọc đóng được tính toán như sau:

N_corr - Số đếm SPT gần mũi cọc đã hiệu chỉnh cho áp lực tầng phủ, s¢_v (búa/300mm);

N - Số đếm SPT đo được (búa/300mm);

D - Chiều rộng hay đường kính cọc (mm);

D_b - Chiều  sâu xuyên trong tầng chịu lực (mm);

q_l - Sức kháng điểm giới hạn tính bằng 0,4N_corr cho cát và 0,3N_corr cho bùn không dẻo (MPa).

* Sức kháng thành bên của cọc trong đất rời, MPa, được lấy bằng:

 (8)

 

2.3. Công thức theo Tiêu chuẩn KGS 2003

Trong Tiêu chuẩn thiết kế kết cấu nền móng của KGS 2003, đưa ra hai công thức tính sức chịu tải cọc. Trong nghiên cứu này giới thiệu công thức 2 như sau:

 

 

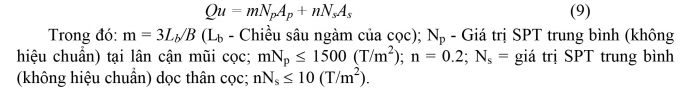 2.4. Hệ số sức kháng cho các công thức

Các công thức trên được sử dụng để ước lượng sức chịu tải cực hạn của cọc. Để áp dụng trong kiểm toán sức chịu tải của cọc cần xác định sức chịu tải tính toán thông qua hệ số sức kháng. Việc xác định hệ số sức kháng cho các công thức có thể hiệu chuẩn từ hệ số an toàn theo phương pháp ứng suất cho phép ASD hoặc phân tích từ lý thuyết độ tin cậy [8].

Trong Tiêu chuẩn AASHTO 2012, hệ số sức kháng cho công thức xác định sức chịu tải cọc đóng thông qua SPT được lấy bằng 0,3 [3]. Hệ số sức kháng này được rút ra từ phân tích thống kê số liệu thử tải cọc của hơn 100 cọc đóng trong chương trình nghiên cứu NCHRP 507  [9]. Trong chương trình này, tất cả các dạng cọc đóng (cọc vuông BTCT, cọc ống BTDƯL, cọc ống thép kín mũi, hở mũi) được phân tích và đưa ra hệ số chung, không có hệ số riêng cho cọc ống thép.

Trong chương trình nghiên cứu năm 2009, Jae Hyun Park và cộng sự đã tiến hành chương trình nghiên cứu “Resistance Factors Calibration and Its Application Using Static Load Test Data for Driven Steel Pipe Piles”. Trong chương trình này đã nghiên cứu phương pháp xác định hệ số sức kháng dựa vào lý thuyết độ tin cậy cho cọc ống thép và áp dụng triết lý thiết kế theo hệ số sức kháng và hệ số tải trọng LRFD vào trong thiết kế. Các hệ số sức kháng của cọc ống thép được xác định dựa vào lý thuyết độ tin cậy sử dụng các kết quả thí nghiệm nén tĩnh cọc. Theo kết quả nghiên cứu này, hệ số sức kháng đối với công thức theo Tiêu chuẩn KGS ở trên được xác định bằng 0,397 tương ứng với độ tin cậy mục tiêu b_T = 2,00 [5].

Đối với công thức theo Tiêu chuẩn Nhật Bản JRA 2002 hiện nay vẫn đang tính toán theo ứng suất cho phép với hệ số an toàn bằng 3,00. Để xác định hệ số sức kháng phù hợp với triết lý LRFD, Đề tài đã thu thập được 29 số liệu thí nghiệm cọc ở Nhật Bản để phân tích theo lý thuyết độ tin cậy [4]. Việc phân tích được dựa vào phương pháp FOSM được tóm tắt như sau:

 3. SO SÁNH CÁC CÔNG THỨC VỚI KẾT QUÁ THÍ NGHIỆM HIỆN TRƯỜNG

Đã tiến hành tính toán so sánh các công thức trên về cả sức kháng cực hạn và sức kháng tính toán đối với một trường hợp cụ thể có số liệu thí nghiệm nén tĩnh. Cọc thí nghiệm có đường kính ngoài là 600m, đóng sâu 61,2m (ngàm vào lớp đất tốt 3 lần đường kính cọc). Trong 2 cọc có một cọc được gắn thiết bị đo biến dạng dọc thân cọc để xác định riêng rẽ sức kháng thân cọc và sức kháng mũi cọc; cọc số 2 được thí nghiệm như các thí nghiệm nén tĩnh thông thường.

Hình 3.1: Sơ đồ bố trí cọc và mặt cắt địa chất

3.1. Kết quả thử tải

Trong quá trình thử tải, mối quan hệ giữa tải trọng - biến dạng được xác định để phân tích ứng xử. Các biểu đồ quan hệ sau đây được thiết lập:

- Đường cong P-S;

- Đường cong Log P-Log S;

- Đường cong S-Log t;

- Đường cong ΔS/Δlogt-P;

- Biểu đồ phân bố chiều sâu - biến dạng;

- Biểu đồ phân bố chiều sâu - lực dọc;

- Biểu đồ phân bố chiều sâu - sức kháng ma sát;

- Biểu đồ phân bố sức kháng ma sát - chuyển vị tương đối.

Trên Hình 3.2 thể hiện biểu đồ biến dạng cọc trục theo độ sâu đối với cọc thí nghiệm 1.

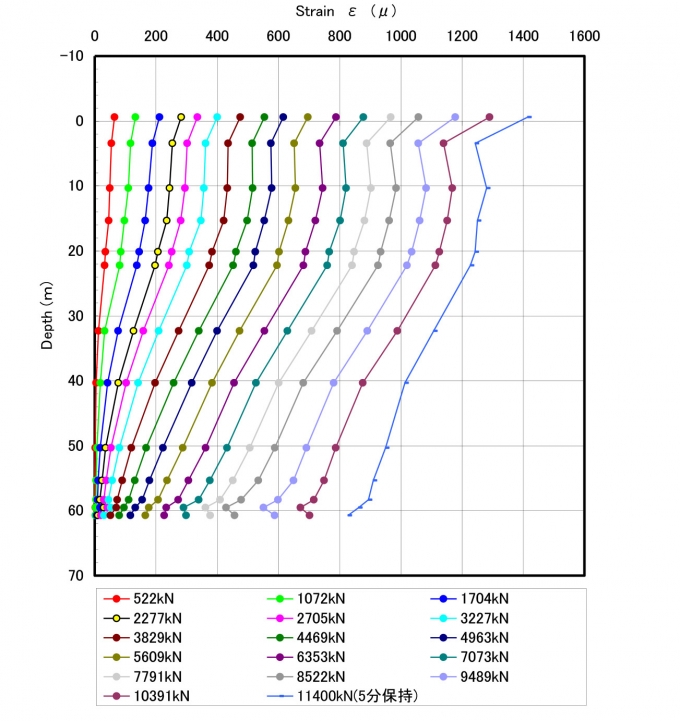Hình 3.2: Biểu đồ phân bố biến dạng cọc trục theo độ sâu cọc 1

Xác định SCT theo phương pháp DeBeer: Mối liên hệ giữa chuyển vị đầu cọc và lực đầu cọc của cọc thí nghiệm 1 được thể hiện trên các đồ thị hai trục logarit. Điểm giao nhau của hai đường thẳng thể hiện sức kháng cực hạn theo phương pháp DeBeer (Bowles, 1996). Điểm này biểu thị điểm thay đổi mà ở đó độ lún tăng lên nhanh chóng. Sức kháng cực hạn đo đạc được trình bày trên Bảng 3.1. Tỷ số sức kháng tổng cộng của cọc thí nghiệm 2/cọc thí nghiệm 1 từ 1,24~1,30.

Bảng 3.1. Sức kháng cực hạn theo phương pháp DeBeer

 

	Sức kháng cực hạn tổng cộng (kN)	Sức kháng thành bên (kN)	Sức kháng mũi cọc (kN)
(1) Cọc thí nghiệm 1	7,553~8,538	3,801 ~ 3,871	3,682 ~ 4,737
(2) Cọc thí nghiệm 2	9,794~10,595	-	-
Tỷ số (2)/(1)	1.24~1.30	-	-

Xác định SCT theo phương pháp JRA (Hiệp hội Đường bộ Nhật Bản): Xây dựng biểu đồ quan hệ giữa chuyển vị đầu cọc và lực đầu cọc và lực mũi cọc. Trong phương pháp JRA, sức kháng cực hạn đo được định nghĩa là tải trọng ở đầu cọc khi chuyển vị đầu cọc đạt 0,1D. Sức kháng cực hạn đo được trình bày trên Bảng 3.2. Tỷ số sức kháng cực hạn tổng cộng của cọc thí nghiệm 2 và cọc thí nghiệm 1 là 1,05.

Bảng 3.2. Sức kháng cực hạn theo phương pháp JRA (tại chuyển vị đỉnh cọc = 0,1D (60mm))

 

	Sức kháng cực hạn tổng cộng (kN)	Sức kháng thành bên (kN)	Sức kháng mũi cọc (kN)
(1) Cọc thí nghiệm 1	7,865	3,849	4,016
(2) Cọc thí nghiệm 2	8,282	-	-
Tỷ số (2)/(1)	1.05	-	-

Việc so sánh sức kháng xác định bởi phương pháp DeBeer và phương pháp JRA được trình bày trên Bảng 3.3. Chúng ta có thể xác định sức kháng đo đạc bằng “7,865kN” tính toán theo phương pháp JRA thiên về an toàn hơn.

Bảng 3.3. Sức kháng cực hạn của cọc thí nghiệm

 

	Thí nghiệm	Sức kháng cực hạn tổng cộng (kN)	Sức kháng thành bên (kN)	Sức kháng mũi cọc (kN)
Cọc thí nghiệm 1	Phương pháp DeBeer	7,553~8,538	3,801~3,871	3,682~~4,737
	Phương pháp JRA	7,865	3,849	4,016
Cọc thí nghiệm 2	Phương pháp DeBeer	9,794~10,595	-	-
	Phương pháp JRA	8,282	-	-

3.2. So sánh với các công thức tính

Trong nghiên cứu này đã sử dụng các công thức trình bày trong mục 2 để tính toán sức chịu tải của cọc theo đúng thực tế thi công và so sánh với kết quả thí nghiệm. Bảng 3.4 và 3.5 thể hiện so sánh kết quả thí nghiệm với kết quả tính toán theo cả 3 công thức trên lần lượt với sức kháng cực hạn và sức kháng tính toán.

Bảng 3.4. So sánh kết quả thí nghiệm với các kết quả lý thuyết (sức kháng cực hạn)

	Thí nghiệm (kN)	Sức kháng lý thuyết
		272-05 (kN)	Tỷ số (2)/(3)	JRA 2002 (kN)	Tỷ số (2)/(5)	KGS 2003 (kN)	Tỷ số (2)/(7)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
Sức kháng tổng	7,865	3,861	2,04	5,532	1,42	4,399	1,79
Sức kháng mũi	4,016	891	4,51	2,030	1,98	1,272	3,16
Sức kháng thành	3,849	2,971	1,30	3,502	1,10	3,127	1,23

Bảng 3.5. So sánh kết quả thí nghiệm với các kết quả lý thuyết (sức kháng tính toán)

	Thí nghiệm (kN)	Sức kháng lý thuyết
		272-05 (kN)	Tỷ số (2)/(3)	JRA 2002 (kN)	Tỷ số (2)/(5)	KGS 2003 (kN)	Tỷ số (2)/(7)
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
Sức kháng tổng	6,292	1,158	5,43	2,584	2,44	1,839	3,42
Sức kháng mũi	3,213	267	12,02	948	3,39	505	6,36
Sức kháng thành	3,079	891	3,45	1,636	1,88	1,334	2,31

3.3. Nhận xét kết quả

Dựa trên các kết quả như trên Bảng 3.4 và 3.5 có đưa ra một số đánh giá về kết quả tính toán sức chịu tải cọc ống thép các công thức khác nhau và theo kết quả thí nghiệm hiện trường như sau:

- Bằng việc sử dụng kết quả thí nghiệm, chúng ta có thể xác định sức kháng thực tế của cọc ống thép.

- Tỷ số giữa sức kháng cực hạn đo đạc chia cho sức kháng cực hạn thiết kế của Tiêu chuẩn 22TCN 272-05 là 2.04; tỷ số tương ứng là 1,42 nếu sử dụng JRA 2002 và 1,79 nếu sử dụng KGS 2003. Tỷ số giữa giá trị thiết kế và giá trị đo đạc, tiêu chuẩn Nhật Bản gần với “1,0” hơn so với 22TCN 272-05. Do đó, sức kháng cực hạn thiết kế của cọc ống thép dựa vào JRA 2002 là phù hợp hơn với sức kháng cực hạn đo đạc trong trường hợp thí nghiệm nén tĩnh cọc ống thép này. Tương tự, sức kháng tính toán theo JRA 2002 cũng gần với sức kháng tính toán theo thử tải hơn so với các công thức khác.

- Về sức kháng thành bên của các công thức là tương đối gần nhau, điểm khác biệt chủ yếu là ở phần sức kháng mũi cọc. Theo kết quả tính toán thì sức kháng mũi cọc theo 22TCN 272-05 là nhỏ nhất, tiếp đó là theo KGS 2003 và cao nhất là theo JRA 2002.

4. MỘT SỐ NHẬN XÉT, KIẾN NGHỊ

Qua các phân tích trên đây có thể rút ra một số nhận xét và kiến nghị như sau:

- Cọc ống thép có rất nhiều ưu điểm và sẽ được áp dụng nhiều trong xây dựng cầu ở Việt Nam trong thời gian tới. Tuy nhiên, ứng xử của cọc, đặc biệt là mũi cọc hở là khá phức tạp, phụ thuộc vào nhiều yếu tố như đường kính cọc, điều kiện địa chất mũi cọc, phương pháp thi công... Vì vậy, các công thức tính toán sức chịu tải cọc ống thép cần phải được phân tích từ các số liệu thí nghiệm hiện trường.

- Kết quả thí nghiệm cọc cho thấy, sức kháng cực hạn của cọc theo công thức JRA 2002 là tương đối phù hợp với thí nghiệm. Tuy nhiên, trong chương trình này mới chỉ tiến hành thí nghiệm 02 cọc, trong một điều kiện địa chất cụ thể nên cũng chỉ đưa ra được nhận xét mang tính tương đối.

- Trong việc thiết kế cọc cho công trình cầu theo triết lý LRFD, ngoài công thức xác định sức kháng cực hạn thì một yếu tố rất quan trọng đó là hệ số sức kháng ứng với công thức đó. Trong 3 công thức trên thì công thức theo Tiêu chuẩn 22TCN 272-05 (cập nhật AAHTO 2012) và KGS 2003, hệ số sức kháng tương ứng đã được phân tích theo lý thuyết độ tin cậy dựa trên các số liệu thí nghiệm thực tế, đảm bảo độ chính xác. Tuy nhiên, chỉ có công thức theo KGS được phân tích chỉ cho các số liệu cọc ống thép, còn trong AASHTO 2012, các số liệu được sử dụng chung cho cả các loại cọc đóng khác nhau. Đối với công thức theo JRA 2002, hiện chưa có hệ số sức kháng tương ứng. Bài báo đã phân tích số liệu của 29 thí nghiệm hiện trường để đưa ra hệ số sức kháng.

Vì vậy, để thiết kế móng cọc ống thép hở mũi cho công trình cầu, trước mắt khuyến nghị áp dụng công thức của KGS 2003 và JRA 2002 với các hệ số sức kháng tương ứng; cần tiếp tục thu thập thêm số liệu thí nghiệm đủ độ tin cậy của Nhật Bản để phân tích hệ số sức kháng theo công thức JRA 2002 dựa vào lý thuyết độ tin cậy.

Tài liệu tham khảo

[1]. Bộ GTVT (2005), Tiêu chuẩn thiết kế cầu 22TCN 272-05.

[2]. Hiệp hội Đường bộ Nhật Bản JRA (2002), Tiêu chuẩn thiết kế cầu đường bộ, phần IV: Kết cấu dưới.

[3]. AASHTO (2010), Specification for LRFD Bridge Design.

[4]. ITST, NSSMC, UTC (2013), Báo cáo kết quả thử tải cọc ống thép.

[5]. Jae Hyun Park  et all (2012), Resistance Factors Calibration and Its Application Using Static Load Test Data for Driven Steel Pipe Piles, KSCE Journal of Civil Engineering.

[6]. Kwangkyum Kim et all (2002), Load Tests on Pipe Piles for Development of CPT Based Design Method, Joint Transportation Research Program, Indiana Department of Transportation and Purdue University.

[7]. FHWA (2006), Design and Construction of Driven Pile Foundations, NHI Courses No. 132021 and 132022.

[8]. FHWA (2001), Load and Resistance factor Design for Highway Bridge Substructures, FHWA-NHI-98-032, U.S Department of Transportation, Washington D.C.

[9]. Paikowsky, Samuel G. (2004), Load and Resistance factor Design for Deep Foundations, NCHRP Report 507, Transportation Research Board, Washington D.C.