Ứng dụng thuật toán bình sai lưới tự do để phân tích độ ổn định của mốc lưới độ cao cơ sở trong trường hợp số lượng mốc không ổn định lớn hơn 50% tổng số mốc trong lưới

Tác giả: ThS. ĐOÀN THỊ BÍCH NGỌC; TS. ĐẶNG XUÂN TRƯỜNG - Trường Đại học Tài nguyên và Môi trường TP. Hồ Chí Minh

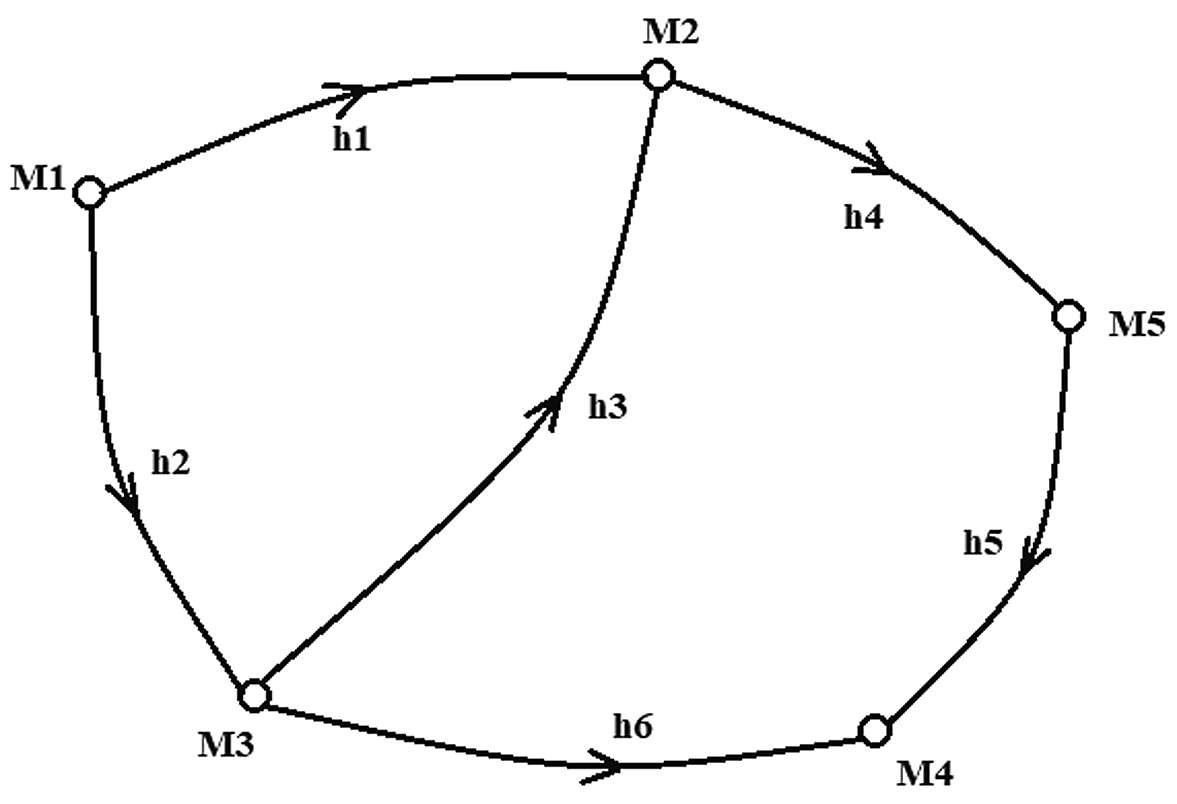Lưới độ cao cơ sở

Hiện nay, cùng với sự phát triển chung của nền kinh tế, các công trình xây dựng với quy mô lớn ngày càng nhiều, những khối nhà với chiều cao hơn 300 m trở nên phổ biến. Do đó, việc xây dựng các công trình nhà cao tầng, khu công nghiệp, công trình cầu… yêu cầu độ chính xác và ổn định cao. Công tác theo dõi và đánh giá mức độ ổn định của các công trình dạng này là một trong những công tác quan trọng và được thực hiện ngay từ giai đoạn đặt nền móng công trình cho đến khi công trình được đánh giá là ổn định. Đặc biệt là các công trình kỹ thuật thuộc dạng có nguy cơ thảm họa cao, nhiệm vụ quan trắc lún tại các công trình mang tính cập nhật thường xuyên với độ tin cậy cao. Do đó, lưới khống chế độ cao cơ sở phải đảm bảo độ chính xác để làm cơ sở quan trắc lún cho công trình đó. Độ ổn định của các mốc cơ sở đóng vai trò quan trọng trong việc đánh giá độ chuyển dịch biến dạng của công trình. Đã có rất nhiều phương pháp được sử dụng để phân tích độ ổn định của hệ thống mốc độ cao cơ sở, nhưng phương pháp được dùng nhiều và mang lại hiệu quả nhất là phương pháp thuật toán bình sai lưới tự do.

Khi dùng thuật toán bình sai lưới tự do để phân tích độ ổn định các mốc cơ sở chu kỳ i (i > 2) trong [1] luôn luôn dùng cao độ bình sai chu kỳ 1 làm cao độ gần đúng (vector độ cao gần đúng H0) để đi tìm trực tiếp các giá trị độ lún của các mốc so với chu kỳ đầu tiên ΔH1-3, ΔH1-4,..., ΔH1-i. Điều này có nghĩa là cao độ trung bình các mốc ổn định chu kỳ sau so với chu kỳ 1 là như nhau. Do đó, nếu số lượng mốc không ổn định tích lũy đến chu kỳ xem xét nào đó vượt quá 50% tổng số mốc trong lưới thì kết luận về tính ổn định mốc sẽ phạm phải sai lầm. Do vậy, ở bài báo này, tác giả tiến hành khảo sát thuật toán bình sai lưới tự do để phân tích độ ổn định của mốc lưới độ cao cơ sở trong trường hợp lưới có số lượng mốc không ổn định lớn hơn 50% tổng số mốc. Cụ thể, bài báo đi khảo sát cả hai trường hợp: lựa chọn vector độ cao gần đúng là độ cao sau bình sai của chu kỳ đầu tiên và lựa chọn vector độ cao gần đúng là độ cao sau bình sai cảu chu kỳ liền kề trước, từ đó đưa ra phương án tối ưu để xử lý được bài toán phân tích độ ổn định mốc một cách tốt nhất.

Mời độc giả xem nội dung đầy đủ bài khoa học tại đây