Áp dụng phương pháp phần tử hữu hạn phân tích tương tác động lực giữa cầu dầm liên tục và xe 3 trục có xét đến lực hãm xe

PGS. TS. Nguyễn Xuân Toản Trường Đại học Bách khoa (Đại học Đà Nẵng) ThS. NCS. Trần Văn Đức Trường Đại học Duy Tân Người phản biện: TS. Cao Văn Lâm PGS. TS. Hoàng Phương Hoa

Tóm tắt: Bài báo giới thiệu kết quả nghiên cứu ứng dụng phương pháp phần tử hữu hạn (PTHH) vào phân tích dao động của cầu dầm liên tục nhiều nhịp dưới tác dụng của tải trọng xe 3 trục theo mô hình tương tác động lực xe-cầu có xét đến lực hãm xe. Kết quả nghiên cứu đối với cầu Hòa Xuân - TP. Đà Nẵng cho thấy lực hãm xe có ảnh hưởng đáng kể đến dao động của cầu.

Từ khóa: Phương pháp PTHH, xe 3 trục, lực hãm xe, tương tác động lực.

Abstract: In this paper presents research results on vibration of the multiple span bridges under three-axle vehicle according to the dynamic interactive model between vehicle and bridge with considering the braking force by the finite element method (FEM). Research results on Hoa Xuan bridge of Danang city show that the braking force effects significantly to the vibration of this bridge.

Keywords: FEM methods, three-axle vehicle, the braking force, the dynamic interactive.

1. Giới thiệu chung

Từ giữa thế kỷ 19, một số nhà khoa học đã bắt đầu nghiên cứu dao động của công trình cầu dưới tác dụng của tải trọng xe di động. Sớm nhất có thể kể đến công trình nghiên cứu được công bố bởi R. Willis (1849) [7]. Ban đầu, các nghiên cứu chỉ tập trung cho phương tiện xe lửa, nhưng càng về sau với sự phát triển mạnh và đa dạng của phương tiện giao thông đường bộ nên đã thu hút được nhiều tác giả nghiên cứu về tác động của các loại xe di động trên cầu theo các mô hình tương tác khác nhau. Đến nay, có nhiều công trình nghiên cứu của các tác giả trên thế giới và trong nước đã được công bố với mô hình tương tác động giữa công trình cầu và tải trọng xe di động ngày càng gần với thực tế hơn. Đáng lưu ý là các nghiên cứu có xét đến ảnh hưởng của lực hãm xe trên cầu [2], [5], [6].

Trong các quy trình thiết kế cầu của nhiều quốc gia đã đề cập vấn đề xem xét ảnh hưởng của lực hãm xe di động theo phương dọc cầu [1], [3]. Tuy nhiên, các quy trình thiết kế chỉ mới phân tích ước lượng lực hãm xe theo phương dọc cầu mà chưa chú ý đến hiệu ứng của lực hãm xe gây ra dao động uốn của dầm trong mặt phẳng đứng. Với xu hướng phát triển của công nghệ vật liệu đã tạo ra nhiều loại vật liệu có cường độ cao và được áp dụng rộng rãi trong xây dựng công trình giao thông, các kết cấu công trình cầu ngày càng trở nên thanh mảnh nên chúng rất nhạy cảm với các tác dụng của tải trọng động nói chung và tải trọng xe di động nói riêng. Khi phanh gấp, xe bị dừng đột ngột trên cầu, lực tương tác giữa các trục xe với mặt cầu thay đổi nên đã gây ra dao động của xe và dao động uốn trong mặt phẳng đứng của cầu cũng tăng lên. Theo kết quả nghiên cứu của các tác giả đã công bố [2], [5], [6], hệ số động lực do tải trọng xe di động, đặc biệt khi xét đến lực hãm xe thường khá lớn. Theo nghiên cứu của nhiều tác giả trên thế giới và trong nước, hệ số động lực lớn hơn đáng kể so với hệ số được sử dụng trong các tiêu chuẩn thiết kế [1], [3].

Trong bài báo, các tác giả giới thiệu kết quả nghiên cứu ứng dụng phương pháp PTHH vào phân tích dao động của cầu dầm liên tục nhiều nhịp dưới tác dụng của tải trọng xe 3 trục theo mô hình tương tác động lực xe-cầu có xét đến lực hãm, trong đó, kết cấu cầu được nghiên cứu là cầu Hòa Xuân - TP. Đà Nẵng gồm 7 nhịp 42m đã liên tục hóa. Tải trọng là xe 3 trục có tốc độ khai thác cho phép trên cầu đến 50km/h và hãm xe gấp tại các vị trí khác nhau ở trên cầu.

2. Mô hình tính toán

Kết cấu cầu Hòa Xuân - TP. Đà Nẵng gồm 7 nhịp 42m được liên tục hóa (Hình 2.1).

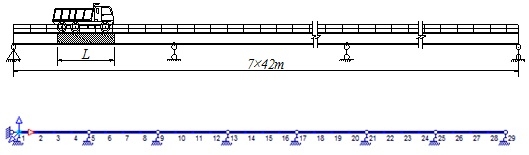Hình 2.1: Sơ đồ cầu Hòa Xuân

Mô hình tương tác động lực giữa phần tử dầm và xe di động có xét đến lực hãm xe như Hình 2.2.

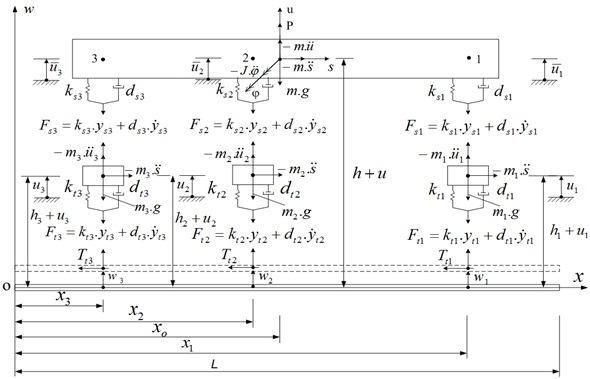Hình 2.2: Mô hình tương tác giữa xe và phần tử dầm

Trong đó:

 

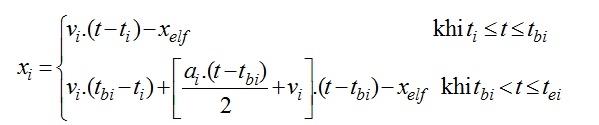   (1)

 

L - Chiều dài của phần tử dầm;

x_o - Tọa độ trọng tâm của xe và hàng trừ trục xe;

x_i - Tọa độ của trục xe thứ i tại thời điểm đang xét;

x_elf - Khoảng cách từ đầu cầu đến đầu trái của phần tử dầm đang xét;

v_i - Vận tốc của trục xe thứ i trước khi hãm xe;

a_i - Gia tốc của trục xe thứ i khi hãm xe (a_i<0);

t­_i - Thời điểm trục xe thứ i bắt đầu vào phần tử dầm;

t­_bi - Thời điểm trục xe thứ i bắt đầu hãm xe;

t­_ei - Thời điểm trục xe thứ i ở điểm cuối của phần tử;

t­ - Thời điểm đang xét;

P = G.sin(Ω.t+α) - Lực kích thích điều hòa. Với Ω - Vận tốc góc, α - Góc pha ban đầu, G - Biên độ;

m - Khối lượng của xe trừ khối lượng của các trục xe;

m_i - Khối lượng của trục xe thứ i;

k_si, d_si - Độ cứng và độ giảm chấn của nhíp xe thứ i;

k_ti, d_ti - Độ cứng và độ giảm chấn của lốp xe thứ i;

s - Quãng đường xe di chuyển;

j - Góc quay của khung xe (rad);

u - Chuyển vị tuyệt đối của khung xe tại khối tâm, tọa độ tuyệt đối của khối lượng m;

   - Chuyển vị tuyệt đối của khung xe tại vị trí trục i;

u_i - Chuyển vị tuyệt đối của trục xe thứ i, tọa độ tuyệt đối của khối lượng m_i;

w_i - Độ võng của dầm tại vị trí của trục xe thứ i;

y_si - Chuyển vị tương đối giữa khung và trục xe thứ i;

y_ti - Chuyển vị tương đối giữa trục xe i và phần tử dầm;

h_i - Khoảng cách tĩnh từ trọng tâm các khối lượng m_i đến trục của phần tử dầm đang xét;

T_ti - Lực ma sát hãm giữa lốp xe thứ i với mặt cầu.

3. Phương trình vi phân dao động phần tử dầm có xét đến lực hãm xe

Phương trình vi phân dao động phần tử dầm có xét đến lực hãm xe được viết dưới dạng ma trận như sau:                                                

     (2)

 

Trong đó:  

    - Lần lượt là véctơ gia tốc, vận tốc, chuyển vị, lực hỗn hợp:

 

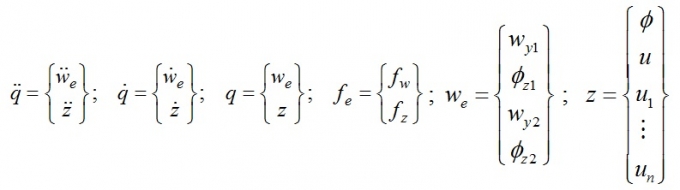    (3)

 

w­_y1, j_z1 - Độ võng và góc xoay đầu trái của phần tử dầm;

w­_y2, j_z2 - Độ võng và góc xoay đầu phải của phần tử dầm;

M_e, C_e, K_e - Lần lượt là ma trận khối lượng, ma trận cản, ma trận độ cứng hỗn hợp:                                                                                           

    (4)

 

Trong đó:                 

       - Ma trận khối lượng, ma trận cản, ma trận độ cứng cơ bản của phần tử dầm chịu uốn, có thể tìm thấy trong tài liệu [4] và [8].

Các ma trận và véc tơ còn lại có thể tìm thấy trong tài liệu [2] và [6].

4. Phân tích dao động của cầu Hòa Xuân bằng phương pháp PTHH

Dựa vào phương trình (2) và áp dụng thuật toán thường dùng trong phương pháp PTHH để xây dựng phương trình vi phân dao động cho toàn hệ (5):

        (5)

 

M, C, K- Lần lượt là ma trận khối lượng, cản và độ cứng hỗn hợp của toàn hệ;

     - Lần lượt là véctơ gia tốc, vận tốc, chuyển vị và lực hỗn hợp của toàn hệ.

Giải phương trình (5) bằng phương pháp Runge-Kutta O(h⁴), Runge-Kutta-Mersion O(h⁵) hoặc Runge-Kutta-Fehlberg O(h⁶) ta tìm được chuyển vị.

Áp dụng công thức (6) để tính hệ số động lực 1+IM:

 

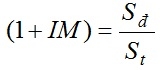(6)

Trong đó: S_đ,S_t - Giá trị chuyển vị động và chuyển vị tĩnh lớn nhất do tải trọng xe di động gây ra có xét đến lực hãm.  

Áp dụng phân tích dao động của cầu Hòa Xuân

- Các số liệu cơ bản của kết cấu cầu

Kết cấu cầu dầm liên tục được mô hình hóa như Hình 4.1, bao gồm các tham số cơ bản như sau: E = 3230769,23T/m², J_d = 0,6879m⁴, F_d = 1,3776m², rF_d = 3,8T/m, q = 0,027, b = 0,01, t = 0,25, g = 9,81m/s².

Hình 4.1: Mô hình PTHH của cầu Hòa Xuân

 

- Các số liệu cơ bản của xe 3 trục

Xe di động là loại xe ASIA có 3 trục (Hình 4.2), có các tham số cơ bản như sau: m = 14,06T, m₁=0,06T, m₂=0,11T, m₃=0,11T, P=0, b₁=3,25m, b₂=1,10m, b₃=2,4m, h= 1,26m,  h₁= h₂= h₃= 0,6m, k_1s=120T/m, k_1t=160T/m, k_2s=k_3s=260T/m, k_2t=k_3t=320T/m, d_1s=0,734Ts/m, d_1t=0,367Ts/m, d_2s=d_3s=0,4Ts/m, d_2t=d_3t=0,8Ts/m.

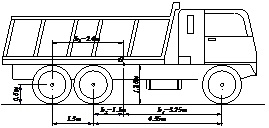Hình 4.2: Xe tải ben 3 trục ASIA

 

- Kết quả phân tích

Tiến hành phân tích dao động cầu Hòa Xuân dưới tác dụng của tải trọng xe ASIA có xét đến lực hãm xe trên cầu bằng phương pháp PTHH và thực hiện khảo sát hệ số động lực (1+IM) của chuyển vị đứng tại các nút nằm trên nửa cầu bên trái khi xe chạy trên cầu với vận tốc ban đầu v=10÷50 km/h và hãm xe tại các vị trí cách gối 1 trên mố một đoạn x=10.5m÷84m.

Kết quả phân tích hệ số động lực (1+IM) khi xét đến hãm xe tại các vị trí khác nhau được thể hiện từ Bảng 4.1 đến Bảng 4.5 và Hình 4.3 đến 4.7.

Bảng 4.1. Hệ số động lực của chuyển vị đứng khi xét và không xét lực hãm xe, v = 10km/h

 

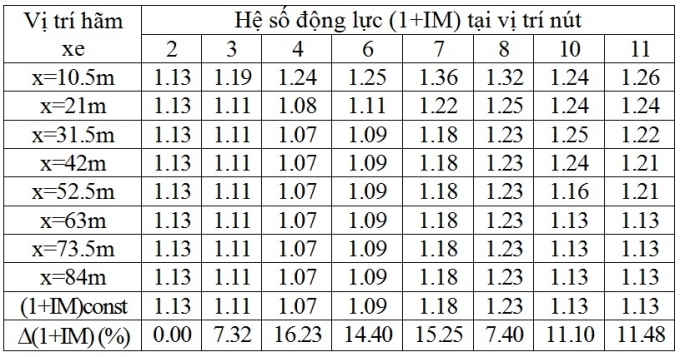Trong đó:

(1+IM)const - Hệ số động lực lớn nhất khi xe chạy qua cầu với vận tốc không đổi, không xét lực hãm xe.

D (1+IM) - Mức tăng của hệ số động lực khi xét đến lực hãm xe so với trường hợp không xét lực hãm xe (%).

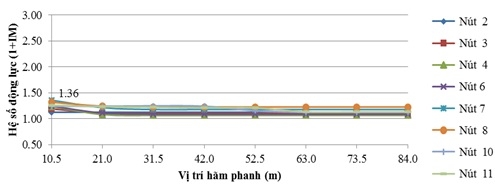Hình 4.3: Hệ số động lực của chuyển vị đứng thay đổi theo vị trí hãm xe khi v = 10km/h

 

Với tốc độ 10km/h, hệ số động lực (1+IM) trung bình là 1,16, trong đó lớn nhất là 1,36 tại nút 7. Mức độ gia tăng hệ số động lực trung bình khi có hãm xe là 10,40%, trong đó mức độ gia tăng lớn nhất khi có hãm xe là 16,23% tại nút 4.

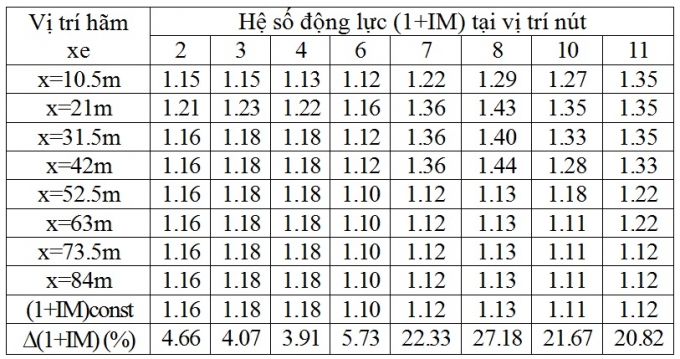
Bảng 4.2. Hệ số động lực của chuyển vị đứng khi xét và không xét lực hãm xe, v = 20km/h

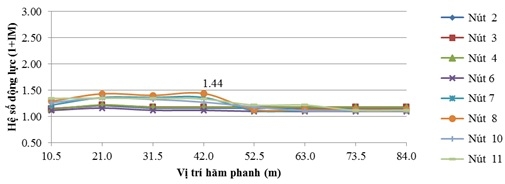Hình 4.4: Hệ số động lực của chuyển vị đứng thay đổi theo vị trí hãm xe khi v = 20km/h

 

Với tốc độ 20km/h, hệ số động lực (1+IM) trung bình là 1,2, trong đó  lớn nhất là 1,44 tại nút 8. Mức độ gia tăng hệ số động lực trung bình khi có hãm xe là 13,80%, trong đó mức độ gia tăng lớn nhất khi có hãm xe là  27,18% tại nút 8.

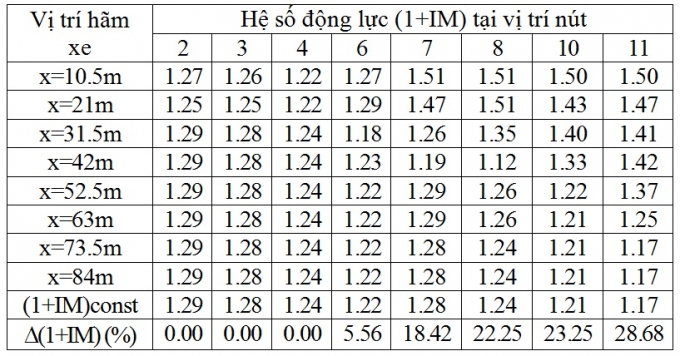
Bảng 4.3. Hệ số động lực của chuyển vị đứng khi xét và không xét lực hãm xe, v = 30km/h

 

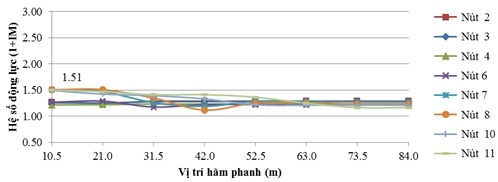Hình 4.5: Hệ số động lực của chuyển vị đứng thay đổi theo vị trí hãm xe khi v = 30km/h

 

Với tốc độ 30km/h, hệ số động lực (1+IM) trung bình là 1,29, trong đó lớn nhất là 1,51 tại nút 8. Mức độ gia tăng hệ số động lực trung bình khi có hãm xe là 12,27%, trong đó mức độ gia tăng lớn nhất khi có hãm xe là 28,68% tại nút 11.

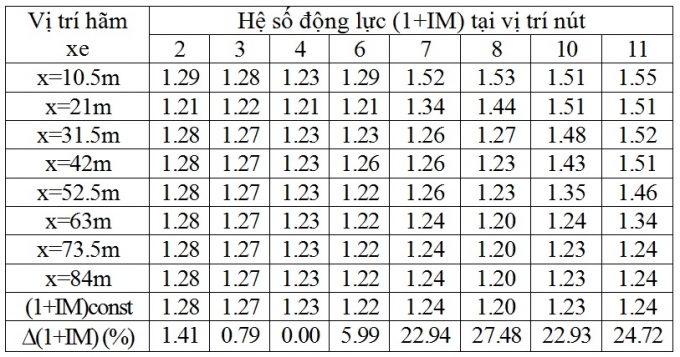
Bảng 4.4. Hệ số động lực của chuyển vị đứng khi xét và không xét lực hãm xe, v = 40km/h

 

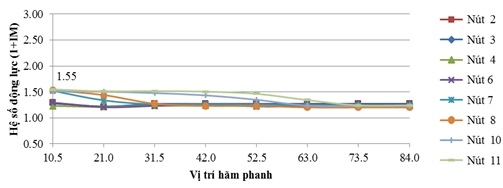Hình 4.6: Hệ số động lực của chuyển vị đứng thay đổi theo vị trí hãm xe khi v = 40km/h

Với tốc độ 40km/h, hệ số động lực (1+IM) trung bình là 1,30, trong đó lớn nhất là 1,55 tại nút 8. Mức độ gia tăng hệ số động lực trung bình khi có hãm xe là 13,28%, trong đó mức độ gia tăng lớn nhất khi có hãm xe là  27,48% tại nút 8.

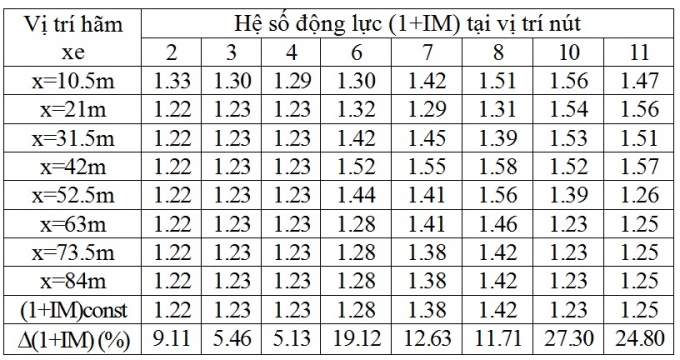
Bảng 4.5. Hệ số động lực của chuyển vị đứng khi xét và không xét lực hãm xe, v = 50km/h

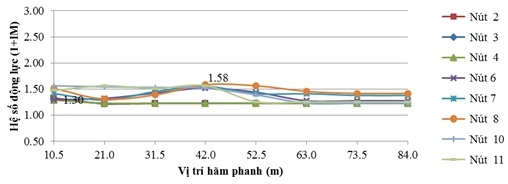Hình 4.7: Hệ số động lực của chuyển vị đứng thay đổi theo vị trí hãm xe khi v = 50km/h

Với tốc độ 50km/h, hệ số động lực (1+IM) trung bình là 1,34, trong đó lớn nhất là 1,58 tại nút 8. Mức độ gia tăng hệ số động lực trung bình khi có hãm xe là 14,41%, trong đó mức độ gia tăng lớn nhất khi có hãm xe là  27,30%.

Qua kết quả phân tích hệ số động lực trên cầu Hòa Xuân do tải trọng xe ASIA chạy với tốc độ v = 10÷50 km/h khi xét và không xét đến lực hãm xe cho thấy: Mức gia tăng hệ số động lực khi có xét đến lực hãm xe so với không xét lực hãm xe là đáng kể, giá trị gia tăng lớn nhất là 28,68%.

5. Kết luận và kiến nghị

Trên cơ sở mô hình tương tác động lực giữa kết cấu cầu dầm liên tục và xe 3 trục có xét đến lực hãm xe, trong đó, xe 3 trục có mô hình bốn khối lượng, có xét đến tải trọng xe, độ cứng và độ giảm chấn của nhíp xe, hệ thống treo, lốp xe, lực ma sát của xe với mặt cầu khi hãm xe. Các tác giả giới thiệu kết quả nghiên cứu dao động của cầu dầm liên tục nhiều nhịp do tải trọng xe di động gây ra có xét đến lực hãm thông qua việc phân tích trực tiếp trên công trình cầu Hòa Xuân, TP. Đà Nẵng bằng phương pháp PTHH. Kết quả cho thấy, mức gia tăng hệ số động lực khi có xét đến lực hãm xe so với không xét lực hãm xe là đáng kể, giá trị gia tăng lớn nhất là 28,68%, vì vậy cần phải lưu ý trong quá trình thiết kế, xây dựng và khai thác cầu o

 

Tài liệu tham khảo

[1]. Bộ GTVT (2005), Tiêu chuẩn thiết kế cầu 22TCN 272-05, NXB. GTVT, Hà Nội.

[2]. Nguyễn Xuân Toản, Trần Văn Đức (2012), Tương tác động lực giữa xe ba trục và cầu dầm liên tục có xét đến lực hãm xe, Tuyển tập Công trình Hội nghị Cơ học toàn quốc lần thứ IX, Hà Nội, tập 1, trang 628-637.

[3]. AASHTO LRFD (2012), Bridge Design Specifications, 6th. ed, American Association of State Highway and Transportation Officials, Washington, DC.

[4]. Ray W. Clough and Joseph Penzien (1993), Dynamics of structures, McGraw-Hill,Inc. Singapore.

[5]. Toan, X.N. (2014), Dynamic interaction between the two axle vehicle and continuous girder bridge with considering vehicle braking forces, Vietnam Journal of Mechanics, vol 36, p49-60.

[6]. Toan X.N, Duc V.T (2014), A finite element model of vehicle - cable stayed bridge interaction considering braking and acceleration, the 2014 World Congress on Advances in Civil, Environmental and Materials Research, Busan, Korea. P.109(20p).

[7]. Willis, R. (1849), The effect produced by causing weights to travel over elastic bars, report of the commissioners appointed to inquire into the application of iron to railway structures, Appendix B, Stationery office, London, England.

[8]. Zienkiewicz, O.C., Taylor, R.L. (2000), The Finite Element Method, 5^th edition, Butterworth-Heinemann, Vol 1&2, Oxford.