Liên hệ quảng cáo
Phương pháp giải và mô phỏng bài toán động lực học ràng buộc điều kiện biên
Hiện nay, các bài toán cơ học có điều kiện biên được rất ít người quan tâm. Bên cạnh đó, các bài toán cơ học nhiều bậc tự do kết hợp với các điều kiện biên thì rất khó khăn trong việc giải bằng tay.
|
TS. Phajm Hoàng Vương Trường Đại học Giao thông vận tải Người phản biện: TS. Lê Lăng Vân TS. Nguyễn Trường Giang |
Tóm tắt: Hiện nay, các bài toán cơ học có điều kiện biên được rất ít người quan tâm. Bên cạnh đó, các bài toán cơ học nhiều bậc tự do kết hợp với các điều kiện biên thì rất khó khăn trong việc giải bằng tay. Thực tế, có nhiều phần mềm có thể mô phỏng chuyển động của một cơ hệ trên máy tính như Catia, Solidworks, TopSolid hay Pro Engineer... nhưng các phần mềm này chỉ giúp người giải quan sát một cách trực quan về sự chuyển động của các khâu trong cơ hệ mà không cho phép tác động vào các khâu trong quá trình mô phỏng. Vì vậy, người dùng không thể ứng dụng các phần mềm này để mô phỏng kết quả của bài toán cơ học có điều kiện biên. Do đó, nội dung của nghiên cứu này là tìm hiểu và ứng dụng phần mềm Matlab vào giải và mô phỏng cơ hệ nhiều bậc tự do có dạng buộc điều kiện biên.
Từ khóa: Động lực học, điều kiện biên, hệ phương trình vi phân chuyển động, mô phỏng matlab.
Abstract: Nowadays, there are little of researchers interested in kinetic with constraint problem. Additional, it is not easy to solve the kinetic with multi degrees of freedom with constraint problem by handing. In pact that, there are a lot of software to simulate motion of mechanical systems as Catia, Solidworks, TopSolid, Pro Engineer ... but its only help solvers to observe motion of mechanical systems without acting simulating results. Therefore, the solvers could not use that software to simulate results of mechanical systems with constraint problem. So that, this research presents a method to solve and simulate mechanical systems with multi degrees of freedom with constraint problem.
Keywords: Kinetics, constraint problem, equations of motion, simulating with matlab.
1. Giới thiệu
Để giải các bài toán động lực học hệ nhiều vật, chúng ta có thể sử dụng rất nhiều phương pháp như: Phương trình Lagrange dạng nhân tử; nguyên lý D’Alembert; phương trình Newton-Euler... Trong nghiên cứu này, tác giả trình bày phương pháp sử dụng phương trình Lagrange dạng nhân tử [1] và xây dựng chương trình tính toán mô phỏng động lực học cho cơ hệ có ràng buộc bởi điều kiện biên trên Matlab. Để giải hệ phương trình vi phân chuyển động này, một phương pháp “Tối thiểu bậc tự do” (Coordinate Reduction Method) [2] được sử dụng. Sau khi giải hệ phương trình vi phân chuyển động, các dữ liệu về vị trí, vận tốc và gia tốc của cơ hệ được sử dụng vào quá trình mô phỏng. Ngoài ra, các phần mền Catia và Matlab cũng được sử dụng để xây dựng mô hình 3D và viết chương trình mô phỏng chuyển động của cơ hệ.
2. Nội dung
2.1. Phương trình Lagrange dạng nhân tử
Xét hệ gồm p vật rắn, f bậc tự do chịu liên kết hôlônôm, giữ, dừng và sử dụng n tọa độ suy rộng q1, q2,…,qn. Phương trình Lagrange dạng nhân tử có dạng:
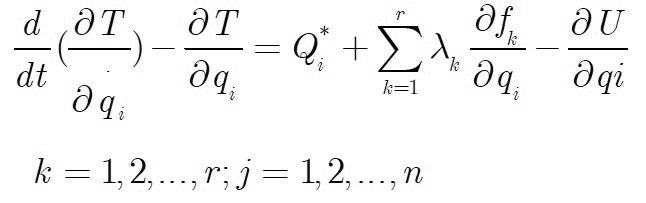 |
(1)
Trong đó:
λk - Nhân tử Lagrange;
fk - Phương trình điều kiện biên;
Q*i - Lực suy rộng ứng với các lực không thế;
T - Động năng của cơ cấu;
U - Thế năng của các lực có thế.
Phương trình (1) là phương trình Lagrange dạng nhân tử tổng quát dùng cho các hệ cơ học. Động năng và thế năng của cơ hệ được tính như sau:
2.1.1 Động năng
Xét cơ hệ gồm p vật rắn, khi đó tổng động năng của cơ hệ có dạng
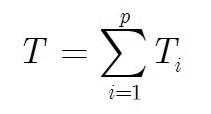 |
(2)
Động năng của khâu i có dạng
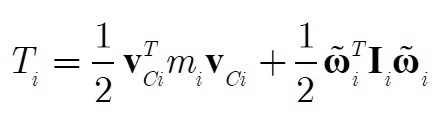 |
| 3 |
(3)
Trong đó:
mi - Khối lượng của khâu i;
VCi - Vận tốc khối tâm Ci;
Ii - Tenxơ quán tính của khâu i trong hệ tọa độ của khâu i;
- Vận tốc của khâu i tính trong hệ tọa độ của khâu i.
2.1.2 Thế năng
Thế năng của các lực có thế tác dụng lên cơ hệ được tính như sau:
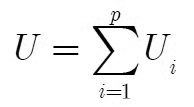 |
(4)
Giả sử rằng các lực có thế tác dụng lên cơ hệ chỉ gồm các trọng lực. Khi đó thế năng của khâu i có dạng:
(5)
Thay phương trình (5) vào (4) ta được
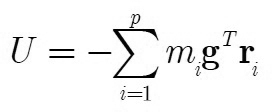 |
(6)
2.2. Phương pháp giảm thiểu bậc tự do khi giải bài toán có điều kiện biên
Đối với với hệ cơ học bất kỳ, hệ phương trình vi phân chuyển động luôn đưa được về dạng như sau:
(7)
Trong đó:
{a} - Ma trận hệ số của thành phần gia tốc;
{b} - Ma trận hệ số của thành phần vận tốc;
{f} - Vector biểu diễn các thành phần ngoại lực và lực thế;
{λ} - Vector hằng số Lagrange có xét đến ảnh hưởng của điều kiện biên đến cơ hệ;
[B] - Ma trận biểu diễn các điều kiện biên.
Vì trong phương trình có chứa vector {λ} nên chưa thể ứng dụng các chương trình giải hệ phương trình vi phân sẵn có của phần mềm Matlab. Để có thể giải được thì vector {λ} cần phải được khử bằng cách tìm ma trận [T] sao cho:
[T].[B]T = [0] (8)
Ma trận [T] là ma trận Null do phần mềm Matlab cung cấp. Khi có ma trận [T] ta tiến hành nhân trái hệ phương trình (7) với ma trận [T], ta có:
(9)
Khi xét tới điều kiện biên của cơ hệ, điều kiện biên của cơ hệ luôn có thể đưa về dạng như sau:
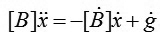 |
| 10 |
(10)
Trong đó: g - Thành phần gồm các hằng số và biểu thức chứa x.
Kết hợp hệ phương trình (9) và (10) ta có:
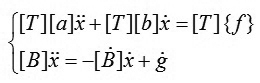 |
| 11 |
(11)
Bằng các ghép ma trận, ta có thể đưa hệ phương trình (11) về dạng sau:
(12)
Trong đó:
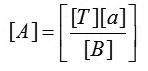 |
(13)
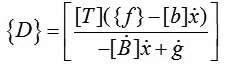 |
(14)
Cuối cùng, hệ phương trình (12) có thể dễ dàng giải được bằng các module giải hệ phương trình vi phân sẵn có của phần mềm Matlab.
2.3. Ví dụ áp dụng
Phương trình động lực học của ví dụ áp dụng đã được trình bày chi tiết trong bài báo “Phân tích chuyển động mô hình xe một bánh 9 bậc tự do” đăng trên Tạp chí GTVT, số tháng 6/2014. Trong bài báo đó, tác giả đã trình bày kết quả mô phỏng chuyển động của xe một bánh 9 bậc tự do với dàng buộc điều kiện biên là điểm P3 chuyển động theo đường tròn có đường kính là 1m. Bài báo này sẽ đưa ra kết quả mô phỏng chuyển động của xe 1 bánh 9 bậc tự do (Hình 2.1) với điều kiện dàng buộc là điểm P3 chuyển động theo một đường thẳng cho trước.
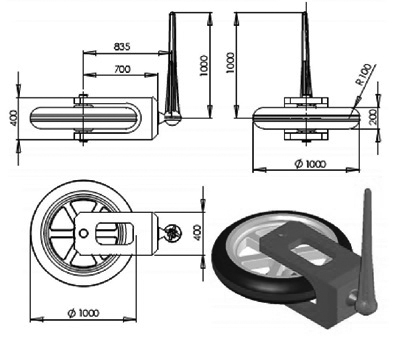 |
| Hình 2.1: Mô hình xe 1 bánh 9 bậc tự do |
Các thông số sử dụng để mô phỏng bài toán như sau:
Khối lượng bánh xe md = 5kg
Khối lượng càng xe là mb = 3kg
Khối lượng con lắc ngược là mp 2kg
Gia tốc trọng trường g = 9,81m/s2
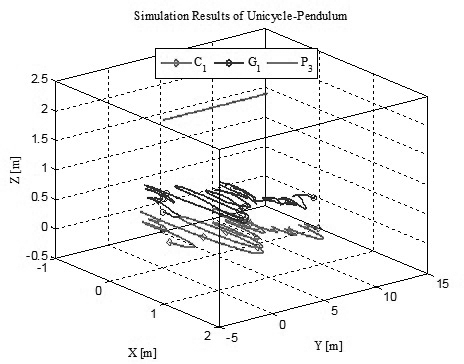
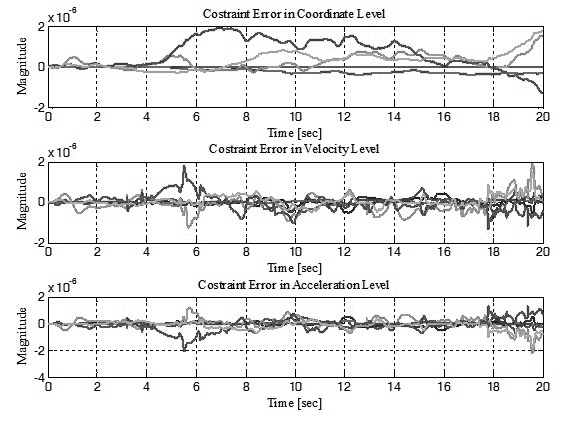
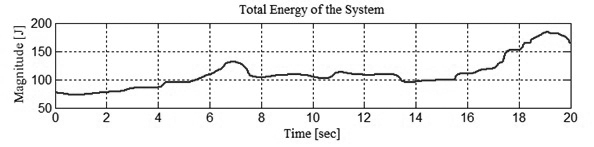
Hình 2.2 mô tả quỹ đạo của các điểm C1, G1 khi điểm P3 chuyển động theo đường thẳng cho trước. Hình 2.3 và 2.4 thể hiện sai số giữa quỹ đạo thực so với quỹ đạo yêu cầu của điểm P3 và quá trình biến đổi năng lượng của mô hình xe một bánh.
 |
|
Hình 2.2: Quỹ đạo chuyển động của điểm C1, G1 và P3 |
 |
|
Hình 2.3: Sai số giữa quỹ đạo thực so với quỹ đạo yêu cầu của điểm P3 |
 |
|
Hình 2.4: Quá trình biến đổi năng lượng của mô hình xe một bánh 9 bậc tự do |
3. Kết luận
Bài báo đã trình bày phương pháp giải và mô phỏng bài toán động lực học cơ hệ có ràng buộc bởi điều kiện biên với việc ứng dụng phần mềm Matlab và công cụ hỗ trợ xây dựng mô hình Catia o
Tài liệu tham khảo
[1]. C.De Boor (1978), A Practical Guide to Spline, Springer-Verlag New York, Inc, New York.
[2]. Farif. M.L. Amirouche (1992), Computational Methods in Multibody Dynamics, The University of Illinois at Chicago.
[3]. Haim Baruh (1999), Analytical Dynamics, WCB McGraw-Hill.
[4]. Hong Sheng Chin (1995), Stabilization methods for simulations of constrained multibody dynamics, The University of British Columbia.
[5]. http://www.mathworks.com.
Tag:






Bình luận
Thông báo
Bạn đã gửi thành công.