Tính toán dao động xoắn tự do của dầm chủ cầu Trần Thị Lý bằng phương pháp giải phóng liên kết trung gian

TS. Trần ngọc An ThS. Lê Tùng Anh Trường Đại học Hàng hải Việt Nam Người phản biện: TS. Hoàng Mạnh Cường                   PGS. TS. Đào Văn Tuấn

Tóm tắt: Dao động xoắn có vai trò quan trọng như dao động uốn trong tính toán cầu treo dây văng và dây võng. Trong bài báo, các tác giả trình bày phương pháp giải phóng liên kết trung gian để tính toán dao động xoắn tự do của cầu Trần Thị Lý.

Từ khóa: Dao động xoắn, hỗ trợ trung gian, cầu Trần Thị Lý.

Abstract: Torsional vibration plays an important role as bending vibration in calculating the cable-stayed bridges and suspension bridges. In this paper, the authors present the intermediate support release method to calculate the free torsional vibration of Tran Thi Ly bridge.

Keywords: Torsional vibration, intermediate support, Tran Thi Ly bridge.

1. Đặt vấn đề

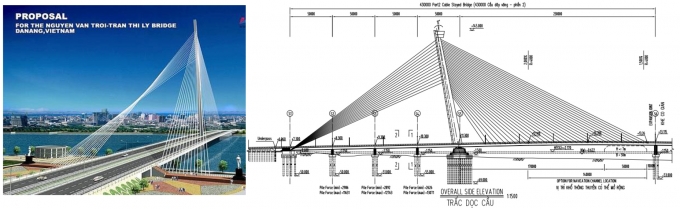
Phương pháp giải phóng liên kết trung gian để tính toán dao động uốn của dầm liên tục do GS. TSKH. Nguyễn Văn Khang đưa ra [4], đã được nhóm nghiên cứu tại trường Đại học Bách khoa Hà Nội tiến hành tính toán dao động uốn tự do và dao động uốn cưỡng bức của dầm liên tục tựa trên các gối cứng và gối đàn hồi trung gian dưới tác dụng của đoàn tải trọng di động [5, 6, 7, 8, 9]. Trong tài liệu [1], T.N.An và L.T.Anh đã trình bày việc mở rộng phương pháp giải phóng liên kết trung gian để tính toán dao động xoắn tự do của thanh thành mỏng, thiết diện không đổi tựa trên các gối cứng, có xét đến hiệu ứng cong vênh. Tính toán dao động uốn tự do và dao động xoắn tự do của thanh thành mỏng có ý nghĩa quan trọng khi xây dựng mô hình mặt cắt 2D trong thí nghiệm hầm gió của cầu nhịp lớn. Trong bài báo, các tác giả trình bày việc áp dụng phương pháp trên để tính toán dao động xoắn tự do cho một mô hình cầu cụ thể, đó là cầu Trần Thị Lý được xây dựng tại Đà Nẵng, Việt Nam. Đây là cây cầu với các nhịp trải dài bắc ngang qua sông Hàn, nối liền quận Hải Châu, quận Sơn Trà và quận Ngũ Hành Sơn. Cầu có nhịp liên tục, được bố trí như sau: 4 nhịp đầu của cầu chính từ mố S1 phía Tây đến trụ S5 (50 mét mỗi nhịp) với tổng chiều dài là 200m. Nhịp chính (nhịp dây văng) từ trụ S5 đến trụ S6 với tổng chiều dài là 230 mét. Bảy nhịp cuối của phần cầu dẫn phía Đông từ trụ S6 đến trụ S13, với tổng chiều dài các nhịp này là 301m [15].

 

Hình 1.1: Hình ảnh và bố trí chung cầu Trần Thị Lý [15]

 

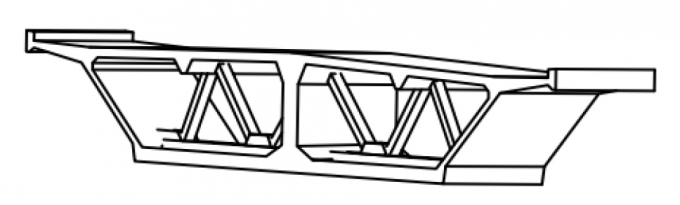Hình 1.2: Mặt cắt ngang cầu điển hình [15]

 

2. Mô hình tính toán và phương trình dao động xoắn tự do

Do phần trụ tháp nằm ở vị trí trụ S5 có góc xoắn bằng 0, mặt phẳng dây văng phía bờ đông nằm ở giữa nhịp dầm và hệ dây văng phía bờ tây nối với bờ cố định nên trụ tháp và hệ dây văng không ảnh hưởng đến dao động xoắn của dầm chủ cầu. Xét mô hình thanh thành mỏng một đầu ngàm, một đầu tựa trên gối cứng như Hình 4.2, phía trong nhịp tựa trên 4 gối cứng trung gian. Dầm chủ cầu có mặt cắt dạng thanh thành mỏng mặt cắt kín nên ta bỏ qua độ cứng chống cong vênh (EI_w = 0).

Hình 2.3: Mô hình nghiên cứu dao động xoắn của dầm chủ cầu Trần Thị Lý

 

Phương trình dao động xoắn tự do của thanh thành mỏng tựa trên các gối cứng trung gian [1]:                                                                                                                                                      

 

 (1)

Trong đó: φ - Góc xoắn của mặt cắt ngang thanh thành mỏng quanh tâm uốn, GI_T - Độ cứng chống xoắn,I_p - Mô-men quán tính cực của mặt cắt ngang lấy đối với trọng tâm của nó, P_b - Khối lượng riêng của dầm, e - Khoảng cách giữa khối tâm và tâm uốn, m - Khối lượng thanh thành mỏng trên một đơn vị dài,a_i - Vị trí gối cứng trung gian thứ i, M^(g)_i   - Phản lực tại gối cứng trung gian thứ I. Hàm δ ( x - ψ) là hàm Delta-Dirac. Hàm này có tính chất:

 

 

 

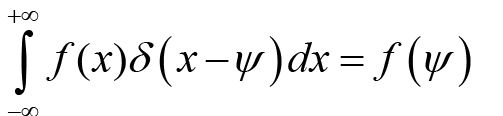Điều kiện hình học tại các vị trí gối cứng trung gian [1]

 với                                                            

 

(2)

Các điều kiện biên (liên kết ngàm và liên kết gối cứng) [1]

 

 (3)

3. Biến đổi hệ phương trình đạo hàm riêng - đại số về hệ phương trình vi phân thường

Áp dụng phương trình Ritz suy rộng và chú ý các điều kiện biên (3), nghiệm của hệ phương trình đạo hàm riêng (1) được tìm dưới dạng:

 

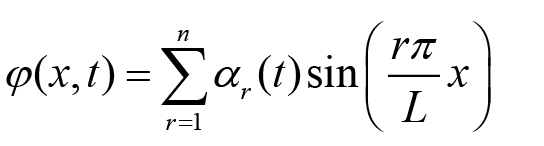  (4)

 

Thế (4) vào (1), ta nhận được phương trình:

  (5)

 

 

Để đơn giản, đặt I =P_bI_P +me² , suy ra:

 

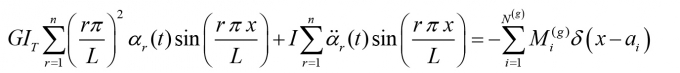  (6)

 

Nhân hai vế phương trình trên với

 

 

 

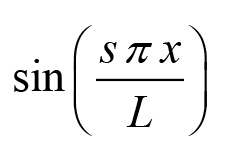rồi tích phân hai vế theo x từ 0 L, phương trình (6) khi đó có dạng:

    (7)

 

 

Xét tích phân ở vế phải của phương trình (7), chú ý hàm Delta-Dirac, ta có:

 

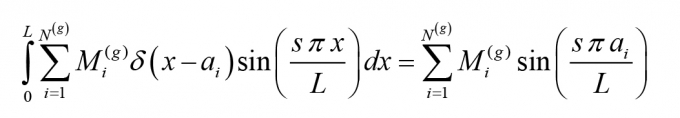(8)

 

Thay (8) vào (7) ta được phương trình vi phân thường:

 

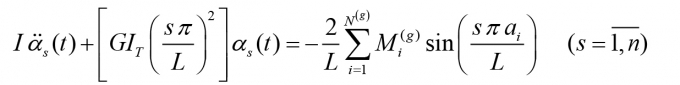   (9)

 

Nếu ta đưa vào ký hiệu:

 

                                                                                                                                                                                             

 

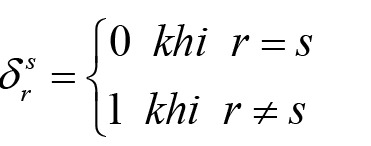Khi đó, phương trình (9) sẽ có dạng:

 

(10)

Để xác định phản lực liên kết tại các gối cứng trung gian, ta viết phương trình (10) dưới dạng ma trận, đặt:

 

                                                                                                                                                                                             

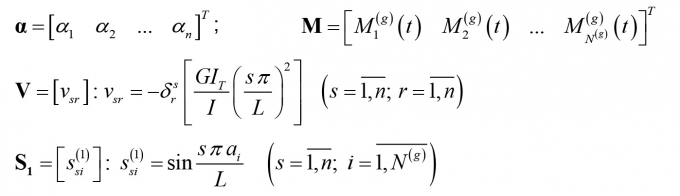Phương trình (10) có dạng:

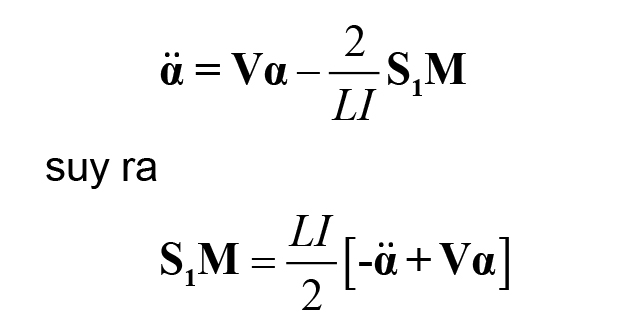 (11)

 

 

(12)

Do ma trận S₁ là ma trận chữ nhật cỡ(n x N^(g)) nên tích S₁ ^T S₁ là ma trận vuông cấp N^(g). Nhân hai vế phương trình (12) với ma trận S^T₁ ta được:

 

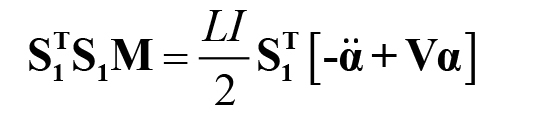 (13)

 

Đặt A = S^T₁S₁ và chú ý rằng, từ điều kiện liên kết 

 

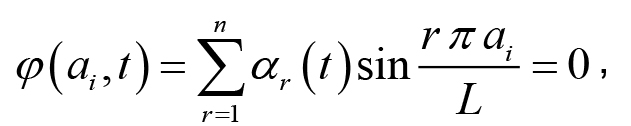  hay                     

 

 

    suy ra        s^T₁`ddota` = 0,

 

từ đó ta có biểu thức xác định phản lực liên kết tại các gối cứng trung gian:

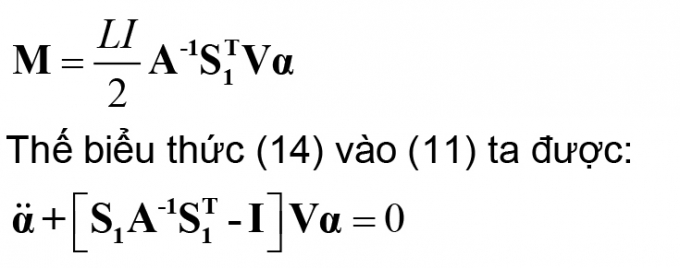(14)

 

 

(15)

 

Trong đó: I - Ma trận đơn vị cấp n. Nếu ta ký hiệu C = [S₁A^-1S^T₁-I] V thì ta nhận được hệ phương trình vi phân thường mô tả dao động xoắn tự do của dầm chủ cầu Trần Thị Lý

 

(16)

hay

 

 

 

 

Giải phương trình đặc trưng tìm các tần số riêng ω, thay vào phương trình (17) tìm các vector riêng α₀.

4. Kết quả tính toán mô phỏng số dao động xoắn tự do của dầm chủ cầu Trần Thị Lý

Bảng 4.1. Các tham số dầm chính cầu [14]

 

Dầm chủ cầu có dạng mặt cắt kín nên theo tài liệu [10], có thể xem tâm uốn trùng với khối tâm, lấy e= 0. Cần chú ý rằng, theo tài liệu [14], trong phần nhịp chính phải bổ sung thêm các thành phần mô-men quán tính khối do mặt lát đường, hệ thống rào chắn... là 728.009,5kgm²/m và 95.540,99kgm²/m.

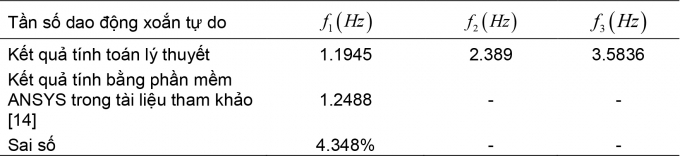
Bảng 4.2. Kết quả tính toán tần số dao động xoắn tự do

 

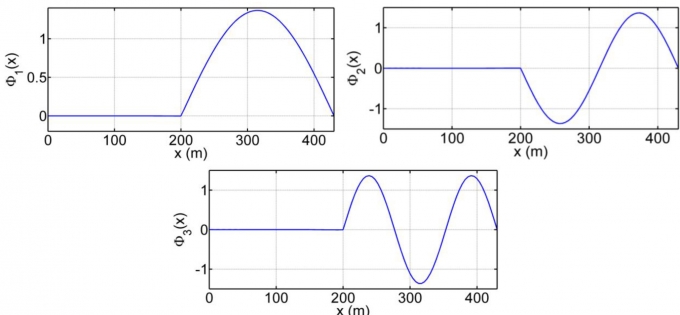Hình 4.1: Đồ thị hàm riêng dao động xoắn ứng với ba tần số dao động xoắn đầu tiên

 

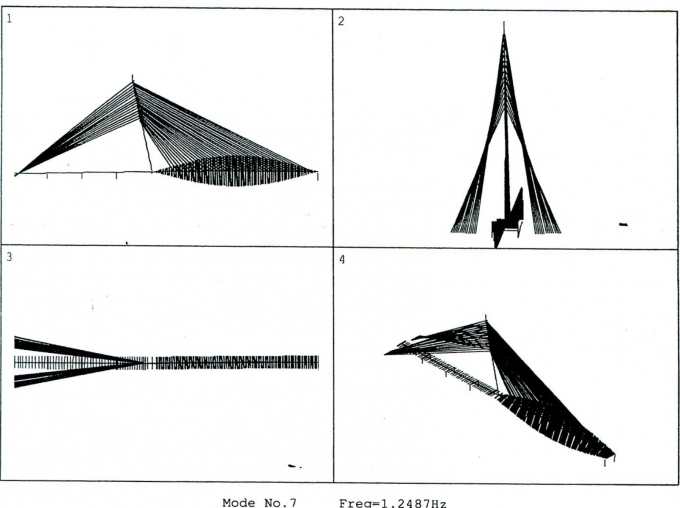Hình 4.2: Mode dao động xoắn đầu tiên của dầm chủ cầu Trần Thị Lý mô phỏng bởi phần mềm ANSYS [14]

 

5. Kết luận

Phương pháp giải phóng liên kết trung gian đã được nhóm nghiên cứu tại Trường Đại học Bách khoa Hà Nội sử dụng để tính toán dao động uốn tự do và dao động uốn cưỡng bức của dầm liên tục tựa trên các gối cứng và gối đàn hồi trung gian [4, 5, 6, 7, 8, 9]. Sự so sánh ưu, nhược điểm của phương pháp giải phóng liên kết trung gian với các phương pháp khác (phương pháp ma trận độ cứng động lực, phương pháp 3 mô-men, phương pháp chuyển vị, phương pháp ma trận truyền và phương pháp phần tử hữu hạn) được trình bày chi tiết trong các tài liệu [8, 9]. Sau đó các tác giả T.N.An và L.T.Anh đã phát triển mở rộng phương pháp giải phóng liên kết trung gian để tính toán dao động xoắn tự do của thanh thành mỏng, thiết diện không đổi, tựa trên các gối cứng, rồi tính toán cho một ví dụ cụ thể [1]. Trong bài báo, các tác giả tiếp tục vận dụng phương pháp giải phóng liên kết trung gian để tính toán dao động xoắn tự do của dầm chủ cầu Trần Thị Lý. Các kết quả tính toán lý thuyết thu được phù hợp tốt với kết quả tính toán bằng phương pháp phần tử hữu hạn (sử dụng phần mềm ANSYS) trong tài liệu tham khảo [14], điều đó khẳng định độ tin cậy của phương pháp đã nêu. Những vấn đề trình bày trong bài báo có thể áp dụng mở rộng để tính toán dao động uốn - xoắn tự do của dầm chủ cầu treo dây văng và dây võng (có xét đến ảnh hưởng của hệ dây treo), dựa trên cơ sở đó tính toán dao động uốn - xoắn dưới tác dụng của tải trọng gió.

Tài liệu tham khảo

[1]. T.N.An, L.T.Anh (2015), Tính toán dao động xoắn tự do của thanh thành mỏng tựa trên các gối cứng bằng phương pháp giải phóng liên kết trung gian,Tạp chí Khoa học Công nghệ Hàng hải, số 42, tr. 63-67.

[2]. T.N.An, N.V.Khang (2012), Tính toán dao động uốn xoắn tự do của dầm khi mặt cắt có một trục đối xứng và chú ý đến hiệu ứng cong vênh, Tuyển tập công trình Hội nghị Cơ học toàn quốc lần thứ 9 (tập 1), tr. 69-78.

[3]. N.V.Khang (2004), Dao động kỹ thuật, NXB. Khoa học và Kỹ thuật.

[4]. N.V.Khang, N.M.Phương (2002), Tính toán dao động uốn của dầm liên tục bằng phương pháp giải phóng liên kết, Tuyển tập công trình Hội nghị Cơ học toàn quốc lần thứ VII (tập 1), pp. 212-219.

[5]. N.V.Khang, N.M.Phuong (2002), Transverse vibrations of continuous beam on intermediate hard and elastic supports under action of moving bodies, Technische Mechanik Magdeburg.

[6]. N.V.Khang, H.Ha, N.M. Phuong (2006), Calculating transverse vibration of beam bridges under action of some moving bodies in Vietnam, Proceedings of the National Conference on Engineering Mechanics and Automation, Bach Khoa Publishing House, Hanoi, pp. 157-171.

[7]. N.V.Khang, N.P.Dien, N.T.V.Huong (2008), Transverse vibration of prestressed continuous beams on ridgid supports under the action of moving bodies, Archive of Applied Mechanics, Springer.

[8]. N.M.Phương (2002), Tính toán dao động uốn của dầm liên tục trên các gối cứng và gối đàn hồi bằng phương pháp giải phóng các liên kết trung gian, Luận văn Thạc sĩ, Trường Đại học Bách khoa Hà Nội.

[9]. N.M.Phương (2009), Tính toán dao động uốn của dầm liên tục và tấm trực hướng hình chữ nhật chịu tác dụng của nhiều vật thể di động, Luận án Tiến sĩ kỹ thuật, Trường Đại học Bách khoa Hà Nội.

[10]. N.V.Trung, P.H.Sơn, V.V.Toản (2006), Cơ sở thiết kế chống gió đối với cầu dây nhịp lớn, NXB. Xây dựng.

[11]. Y.Matsui, T.Hayashikawa (2001), Dynamic stiffness analysis for torsional vibration of continuous beams with thin-walled cross-section, Journal of Sound and Vibration, 243(2), pp. 301-316.

[12]. T. Hayashikawa (1997), Torsional vibration analysis of suspension bridges with gravitational stiffness, Journal of Sound and Vibration, 204(1), pp. 117-129.

[13]. V. Z. Vlasov (1961), Thin-walled elastic beams (2nd ed.), (Translated from Russian), Israel Program for Scientific Translations, Jerusalem.

[14]. Tongji University, Shanghai, PR China (2011), Wind Tunnel Testing of Tran Thi Ly Bridge of Da Nang City, SR Viet Nam, Issue No.1 & No.2.

[15]. http://www.cautranthily.com/vi/.