Phân tích ứng suất tấm bê tông xi măng sử dụng trong mặt đường ô tô và sân bay

TS. Phạm Thị Toan Trường Đại học Giao thông vận tải  Người phản biện: PGS. TS. Cao Trọng Hiền

Tóm tắt: Trong thiết kế mặt đường cao tốc hoặc mặt đường bê tông xi măng (BTXM) là mô hình giống như tấm mỏng Kirchhoff với các điều kiện biên tựa tự do. Bài báo trình bày cách giải phương trình vi phân cân bằng của tấm mỏng đặt trên nền đàn hồi với mô hình nền Winkler và tìm được nghiệm chính xác của độ võng thỏa mãn các điều kiện biên, từ đó tính toán ứng suất trong tấm BTXM. Phương pháp nghiên cứu ở đây là phương pháp M.Lêvi.

Từ khóa: Ứng suất, phương trình vi phân, đàn hồi, độ võng.

Abstract: In designing the highway surface or cement concrete pavement is thin plate-like model with simply supported boundary conditions the eclassical Kirchhoff. This paper presents solutions of governing differential equations of equilibrium thin plate placed on the elastic Winkler foundation model and find the explicit solutions of deflections satisfy the boundary conditions. Since then calculates stresses in concrete plate. Research methodology here is the method M.Levi.

Keywords: Stress, equation, elasticity, deflection.

1. Giới thiệu

Trong dự án xây dựng công trình giao thông thì tính toán kết cấu là một trong những nội dung quan trọng của thiết kế và kiểm định chất lượng, độ bền khai thác và giá thành hợp lý. Nghiên cứu tấm nói chung và đặc biệt là các tấm BTXM được ứng dụng nhiều trong thực tế. Tuy nhiên, các bài toán về tấm thường là khó do tính phức tạp và tìm nghiệm chính xác đòi hỏi những kiến thức rộng về toán. Trong thực tế, nghiên cứu tấm bê tông hình chữ nhật trên nền đàn hồi là cấp thiết được áp dụng trong các kết cấu công trình. Các phương pháp số như phương pháp phần tử hữu hạn, phương pháp phần tử biên được nhiều nhà khoa học áp dụng. Tuy nhiên, bài toán là khó để thu được lời giải chính xác thỏa mãn cả phương trình vi phân cân bằng và các điều kiện biên. Bài báo đã tìm được nghiệm chính xác của bài toán và tính toán ứng suất trong tấm BTXM. Phương pháp nghiên cứu ở đây là phương pháp M.Lêvi. Trong thiết kế mặt đường cao tốc hoặc mặt đường BTXM là mô hình giống như tấm mỏng Kirchhoff với các biên tựa trên chu vi chữ nhật. Bài báo trình bày cách giải phương trình vi phân của tấm mỏng bằng vật liệu BTXM đẳng hướng trên nền đàn hồi theo mô hình nền của Winkler.

2. Giải bài toán

Xét tấm đẳng hướng trên nền đàn hồi, phương trình vi phân cân bằng của tấm có dạng

 

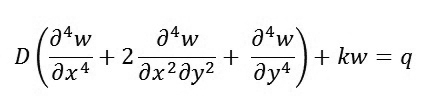(1)

 

 

Trong đó: q - Tải trọng phân bố trên mặt tấm, k - Hệ số nền.

 , E - Mô đun đàn hồi, h - Chiều dày của tấm, v - Hệ số Poisson.

 

 

Điều kiện biên tựa tự do trên chu vi chữ nhật

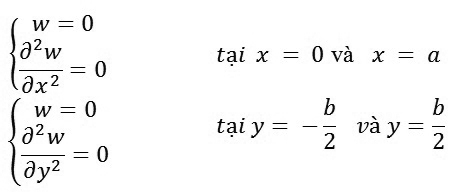 (2)

 

(3)

 

 

Trong đó: a và b - Chiều dài các cạnh của tấm.

Sử dụng toán tử Laplace kép

 

 

 

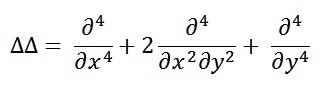Phương trình (1) trở thành

 

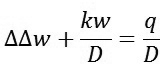(4)

 

Để giải phương trình số (4), ta tìm nghiệm dưới dạng chuỗi

 

(5)

Trong đó: w₁ - Nghiệm riêng của phương trình (4)

 

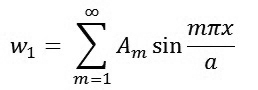(6)

 

Nghiệm w₂  là theo phương pháp của M.Lêvi.

 

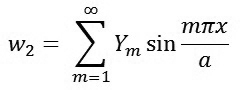(7)

 

Ta có thể biểu diễn tải trọng dưới dạng chuỗi

 

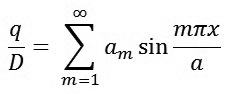(8)

 

 

Lấy đạo hàm riêng công thức (6) , kết hợp với công thức (8) thay vào phương trình (4) ta nhận được :

 

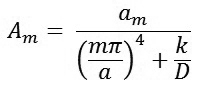(9)

 

 

Để tìm a_m ta nhân cả hai vế của phương trình (8) với          

 và tiến hành lấy tích phân từ 0 đến a và lưu ý do tính đối xứng của nghiệm m chỉ nhận các giá trị lẻ, ta có:

 

 

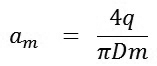(10)

 

Thay (9) và (10) vào (6) ta nhận được

 

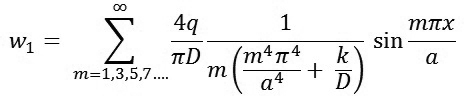(11)

 

Chuỗi trong biểu thức của w₂ là nghiệm của phương trình thuần nhất

 

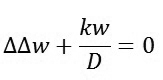(12)

 

Thay biểu thức (7) vào (12) ta nhận được phương trình vi phân

Ký hiệu :

 

(13)

 

 

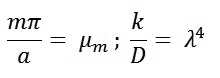(14)

 

 

 

(15)

 

ta nhận được nghiệm

 

(16)

Và độ võng của tấm là :

 

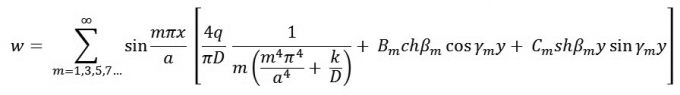(17)

 

Dưới tác dụng của tải trọng phân bố đều, mặt võng sẽ đối xứng qua các trục.

Lúc này, tất cả các số hạng trong chuỗi có giá trị m là chẵn đều mất đi vì chúng đối xứng qua các trục kể trên. Biểu thức (17) thỏa mãn điều kiện biên (2). Để tìm các hằng số B_m và C_m ta thay (17) vào điều kiện biên (3), ta nhận được kết quả:

 

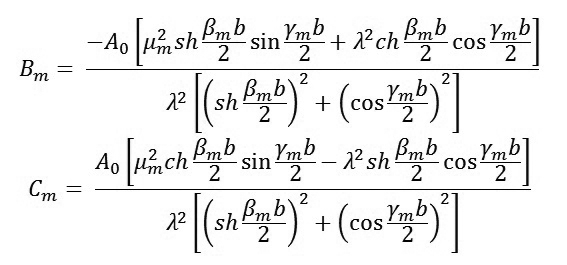(18)

 

 

 

 

Trong đó:

 

 

 

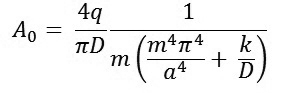Độ võng lớn nhất của tấm tại:

 

 

 

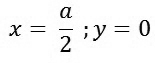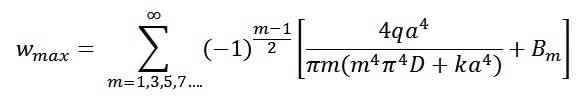 (19)

 

 

 

Xét tấm bê tông với các thông số như sau: a = 300 cm; b = 400 cm; h = 25 cm.

 

 

Thay các thông số này vào công thức (19) ta nhận được

 

 

Nhận xét: Kết quả trên cho thấy chuỗi trong biểu thức hội tụ rất nhanh và từ số hạng thứ 3 có giá trị rất nhỏ.

Mô men uốn của tấm được xác định theo công thức sau:

 

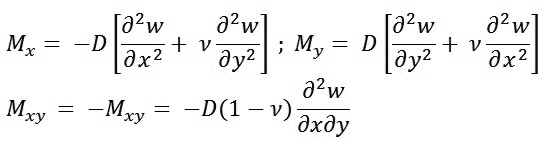(20)

 

 

 

Tại vị trí chính giữa của tấm (x = a/2; y =0) thì mô men là lớn nhất. Thay (17) vào (20) ta nhận được:

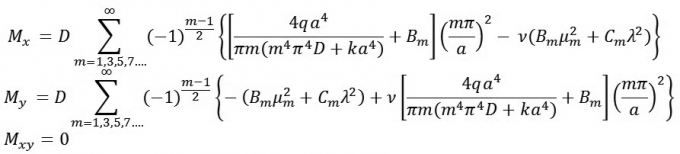   (21)

 

 

 

 

Thay các thông số của tấm bê tông ở trên ta có:

 

 

 

Từ đó ta tính được ứng suất lớn nhất:

 

 

 

 

 

 

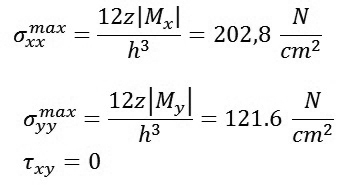3. Kết luận

Bài báo trình bày bài toán tấm đẳng hướng trên nền đàn hồi theo mô hình nền Winkler với điều kiện biên tựa trên chu vi chữ nhật. Trình bày cách giải bài toán tìm độ võng theo phương pháp M.Lêvi, từ đó tính mô men, ứng suất của tấm. Áp dụng tính cho tấm bê tông, xi măng với các số liệu cụ thể.

Tài liệu tham khảo

[1]. Nguyễn Quang Chiêu, Lã Văn Chăm (2001), Xây dựng nền đường ô tô, NXB. GTVT, Hà Nội.

[2]. Nguyễn Văn Khang (1998), Dao động kỹ thuật, NXB. Khoa học và Kỹ thuật, Hà Nội.

[3]. Nguyễn Xuân Lựu (2008), Lý thuyết đàn hồi, NXB. GTVT, Hà Nội.

[4]. Bull.Soc.Philmath (1823), Pari.

[5]. Hardcover (1939), Tables of circular and hyperbolic sines and cosines, NewYork.

[6]. Ian.H.Sneddon (1972), The Use of Integral Transforms, McGraw - Hill Inc.

[7]. Ian.H.Sneddon (1981), The Applicarion of Integral Transform in Elasticity, McGraw - Hill Inc.

[8]. J.W.S Rayleigh (1945), The Theory of Sound, Dover Publications Inc, New York.

[9]. R.B.Bhat, C.Rajalingham and G.D.Xistris (1997), Vibration of rectangular plates by reduction of the plate partial differential equation into simultaneous ordinary differential equations, Journal of Sound and Vibration203 .

[10]. S.Timoshenko (1940), Theory of plates and shells - Mc Graw - Hill, Company Inc, New York.

[11]. Nguyễn Quang Chiêu, Lã Văn Chăm (2001), Xây dựng nền đường ô tô, NXB. GTVT, Hà Nội.

[12]. Nguyễn Văn Khang (1998), Dao động kỹ thuật, NXB. Khoa học và Kỹ thuật, Hà Nội .

[13]. Nguyễn Xuân Lựu (2008), Lý thuyết đàn hồi, NXB. GTVT, Hà Nội

[14]. Bull.Soc, Philmath (1823), Pari.

[15]. Hardcover (1939), Tables of circular and hyperbolic sines and cosines, NewYork.

[16]. Ian.H.Sneddon (1972), The Use of Integral Transforms, McGraw - Hill Inc.

[17]. Ian.H.Sneddon (1981), The Applicarion of Integral Transform in Elasticity, McGraw - Hill Inc .

[18]. J.W.S Rayleigh (1945), The Theory of Sound, Dover Publications Inc, New York.

[19]. R.B.Bhat, C.Rajalingham and G.D.Xistris (1997), Vibration of rectangular plates by reduction of the plate partial differential equation into simultaneous ordinary differential equations, Journal of Sound and Vibration203.

[20]. S.Timoshenko (1940), Theory of plates and shells - Mc Graw - Hill, Company Inc, New York.